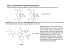Chiral Minimal Surface Geometries for Photonic Crystal Design

Chiral Minimal Surface Geometries for Photonic
Crystal Design
Matthias Saba1 , Anna-Lena Robisch1, Michael Thiel2 ,
Klaus Mecke1 , and Gerd E. Schröder-Turk1,∗
1
Institut für Theoretische Physik, Friedrich-Alexander Universität Erlangen-Nürnberg,
Staudtstr. 7, 91058 Erlangen, Germany
2
Angewandte Physik & Center for Functional Nanostructures, Karlsruhe Institute of
Technology, 76128 Karlsruhe, Germany
∗
E-mail: Gerd.Schroeder-Turk@physik.uni-erlangen.de
October 22, 2010
A spatial structure for which mirror reflection cannot be represented by rotations and translations is chiral. For photonic crystals and metamaterials,
chirality implies the possibility of circular dichroism, that is, that the propagation of left-circularly polarized light may differ from that of right-circularly
polarized light. The dominant chiral geometric element in current designs are
one-dimensional helical spirals or chiral stackings of straight rods, arranged
on a lattice. Here we draw attention to chiral sheet- or surface-like geometries based on chiral triply-periodic minimal surfaces. Specifically we analyse circular polarization effects for two photonic crystal designs based on the
so-called C(Y) minimal surface of cubic symmetry, by band structure analysis and by scattering matrix calculations of the reflection coefficient; a chiral
photonic crystal given by two silicon network domains shows a circular polarisation band gap, whereas the chiral photonic crystal given by a sheet of
1
uniform thickness draped onto the C(Y) minimal surface shows almost no circular dichroism at all.
Structural chirality has been recognized as an important design feature for photonic crystals
and optical metamaterials, e.g. to obtain negative refraction and for circular-polarization filters
[1, 2, 3], and it is realised in biological photonic crystals in butterflies [4, 5]. However, there are
several distinct routes to structural chirality, such as by arranging achiral elements in a globally
chiral symmetry group, or vice versa, by decorating the point sites of an achiral symmetric lattice by chiral elements. The elements maybe quasi one-dimensional objects, e.g. line segments
or spirals, or two-dimensional surface patches. The resulting chiral material may be composed
of disconnected components or form continuous percolating chiral domains. The chirality may
be a purely geometry property, in the sense that the material can be continuously deformed
to an achiral structure without tearing or glueing, as is the case for parallel single- or doublehelices that can be deformed to achiral straight rods; chirality can also be a homotopic property
if entanglement or knotting prohibits deformation to an achiral geometry. A chiral structure is
also not necessarily ordered or periodic, but may be disordered or may be an achiral structure
with few isolated chiral defects. The situation is further complicated by the lack of a continuous or gradual measure of structural chirality to discern between different degrees of chirality
of a given structure. For the current geometric discussion, chirality is a geometric on/off property: a structure is either chiral if it is not congruent to its mirror image, or otherwise it is achiral.
1 The chiral triply-periodic C(Y) minimal surface
Triply-periodic minimal surfaces (TPMS) are surfaces of vanishing mean curvature that are periodic with three linearly-independent lattice vectors. These surfaces divide space into exactly
two domains, with the minimal surface as their joint and only interface. The individual domains
2
each are a continuous component, percolating through space. They are often represented by the
one-dimensional network graph that traces the center-lines of the labyrinthine domain. Particularly well-known are the cubic Gyroid [6], Primitive and Diamond surfaces [7]; however, many
more TPMS exists, both of cubic [6, 8] and of lower symmetries [9, 10].
The C(Y) TPMS is balanced, that is, rotations exist that map the infinite surface onto itself
and that exchange the two labyrinthine domains. As an oriented surface (that is, for example
if its two sides are colored differently or one of the labyrinths is solid and the other void) it
has simple cubic symmetry P 4332 (Fig. 1, top). As an unoriented surface (that is uncolored
and without point normals or other features that distinguish inside and outside) it has bodycentered cubic symmetry I41 32. This is the space group of the thickened surface sheet and of
the double-graphs in Fig. 1 (bottom). The unoriented and the oriented surface are both chiral.
As the operation that exchanges the two labyrinthine domains is a two-fold rotation, the two
network domains are of the same handedness (in contrast to e.g. the inversion symmetry that
exchanges the two srs networks of different handedness in the achiral Ia3d Gyroid).
A cubic translational unitcell of the unoriented C(Y) TPMS in its symmetry group I41 32 is
built from a smaller surface patch by applying symmetries. A convenient choice is the surface
patch bounded by the straight line polygon with vertices {(0,1/4,1/8), (0,1/4,5/8), (1/8,3/8,5/8),
(1/8,0,1/4)} plus 2π/3 and 4π/3 rotations thereof around the [111] axis. (This patch has threefold symmetry, hence the asymmetric patch is smaller but is not bounded by straight lines).
The body-centered translational translational unit cell is obtained by applying all symmetries
of I41 32, except for the [111] three-fold rotations. Note that the orientation (i.e. crystallographic coordinates) and size of the body-centered I41 32 unit cell of the non-oriented surface
is the same as the primitive cubic P 43 32 unit cell of the oriented surface. The corresponding
3
43
21
43
41
Figure 1: The chiral strut-like (P 43 32, top) and sheet-like (I41 32, bottom) designs derived from
the triply-periodic C(Y) minimal surface. Also shown are the structures clipped to a cylinder
around the two distinct screw axes for each symmetry group along [100]. These are 43 and 21 for
P 42 32 and 41 and 43 for I41 32. Skeletal graphs that trace the channel center lines are depicted
by bars and spheres.
skeletal graphs tracing the center lines of the labyrinthine domains can be computed by the
medial surface construction [11, 12]. Each graph has three distinct three-coordinated nodes A:
(5/8,3/8,7/8), B : (0.225,0.275,0.725) and C: (3/8,3/8,5/8) and two edges (A,C) and (B,C); this
yields both graphs if embedded in I41 32 (no. 214 in [13]), or a single graph if embedded in
4
P 43 32 (no. 212), with the conventional choice of origin. The smallest ring has eight edges.
Based on the C(Y) minimal surface a number of photonic crystal designs can be derived:
Space can be partitioned, with symmetry P 43 32, into two congruent like-handed domains on either side of the minimal surface of different dielectric constant, see Fig. 1 (top). For brevity, we
will refer to one of the domains as solid and the other as void. Structures obtained by inflating
a single C(Y) graph to a solid tubular network also have symmetry P 43 32; the tubular radius
r determines the solid volume fraction. The maximal filling fraction Φ that can be obtained
while maintaining the network topology is ≈ 90% (r = 0.25 a). A related structure is obtained
by a parallel body construction where one of the minimal surface domains are set as the solid
phase and in addition that fraction of the other domain that is closer than a given value r to the
minimal surface; For r ≤ rs ≈ 0.06 a (Φ ≈ 75%) the interface is a smooth parallel surface to
the C(Y) minimal surface without cusps; the maximal value of r which maintains the topology
of a single labyrinthine domain is r ≈ 0.085 a (Φ = 84%). Similarly, a solid/void partition
of space on either side of a constant mean curvature companion surface to the C(Y) minimal
surface result by minimizing interface area while maintaining fixed volume and topology [14].
CMC companion surfaces to the C(Y) surface can be realized such that the smaller of the resulting domains, resembling the C(Y) graph, occupies 5% of the total space (corresponding to
mean curvature H0 ≈ 10/a with the cubic lattice length a); the existence of CMC companion
surfaces with even smaller volume fractions is difficult to assert without better mesh refinement
methods. All of these structures have the same symmetry P 43 32 and are topologically equivalent to a single C(Y) graph.
Geometries with the symmetry I41 32 of the non-oriented C(Y) minimal surface and that of
two C(Y) graphs are: The C(Y) minimal surface is inflated to a solid sheet of constant thickness
5
(bounded by two parallel surfaces with distance ±r), leaving two unconnected network-like
void domains (analysed in Fig. 3). The geometric shape of the interface may again be altered,
to be either given by CMC surfaces (in which case the thickness of the sheet is no longer constant) or by tubular representations of the skeletal network. Of the same symmetry are structures
consisting in two network-like solid domains separated by a void matrix, with the same interface types possible as above.
The different local chiral elements of these geometries are demonstrated in Fig. 1. For the
I41 32 C(Y) geometries there are two symmetrically distinct four-fold screw axes along the [100]
directions (plus three-fold screws along the body diagonals not discussed here), one left-handed
(LH) and one right-handed (RH). However, their local geometry is different hence breaking the
symmetry between the two hands. While the LH screw corresponds locally to a continuous
helicoid-like surface patch along the rotation axes (also evidenced by the double helix shape of
the two skeletal graphs), the RH screw axis locally maps surface patches perpendicular to the
rotation axes and is topologically discontinuous (corresponding to the dog-bone stacking of the
corresponding skeletal graph elements). For the P 43 32 geometry, a single LH 43 screw axis
exist, corresponding to a single-helix structure around the rotation axis. The axis corresponding
to the RH dog-bone 41 screw of the I41 32 geometry is an achiral 21 screw axis for the P 4332
geometry, neither LH nor RH.
2 Circular-polarization effects in C(Y) photonic crystals
Photonic band structures and transmission coefficients are computed on voxelized binary data
sets.1 These are obtained from triangulations of the C(Y) minimal and constant mean curva1
1283 voxels per cubic unit cell for scattering matrix calculations; 5123 voxels per primitive unit cell along
with a discrete Fourier grid of size 643 for MPB
6
C
β
|k|
R
1
0.9
ω4
ωa/2πc
0.8
ω3
0.7
ω2
0.6
ω1
0.5
A
B
0.4
-0.8 -0.4
0
C
0.4 0.8 Γ
H
0.2
D
0.6
10
RCP
LCP
0.5
1
Figure 2: Circular polarization analysis for a structure based on two silicon network domains
bounded by C(Y) CMC surfaces in a void matrix. This is topologically the complement of the
structure shown at the bottom of Fig. 1. The volume fraction of the dielectric is ϕ = 21.4%. The
y-axes represent the frequency in dimensionless units. The x-axis are: A The circular dichroism
index C (eq. 1), B the absolute value of the corresponding wave vector k in [100]-direction from
Γ-point to the Brillouin-zone edge, C the coupling index β (eq. 2) and D the reflectance rate
R. Modes with |C| > 0.5 are called circular-polarized and modes with β < 0.1 are called low
coupling. Red [blue] color is for right [left] circular polarization. A-C The color represents the
value of C, point size the value of β.
ture surfaces computed by conjugate gradient minimization using Surface Evolver [15]. The
minimal surface is computed by surface area minimization of the surface patch bounded by
in-surface straight lines and application of symmetries. The CMC surfaces are obtained by
R
minimization (to zero) of the surface integral S (H(p) − H0 )2 dp (with point-wise mean curvature H(p) and prescribed parameter H0 ) for the translational unit cell with periodic boundary
conditions; the symmetry is only implicitly fixed by starting from a coarse triangulated mesh
with the desired symmetry.
7
Circular dichroism as a function of frequency is characterized by reflectance rates computed
by a scattering matrix approach [16] and by analysing the degree of circular polarization of the
magnetic eigenfields of a band structure for infinite crystals [17, 18]. For the latter approach,
coupling amplitudes
2
Z
1
C± = R
dx dy (ex ± ıey ) · Hk,n (r)
dx dy
of an incident circularly-polarized plane wave (ex ± ıey ) eıqz (with ı =
√
−1) with the crystal
modes Hk,n (r) are computed in an xy-plane perpendicular to the wave-vector of the incoming
wave q = qez . The circular dichroism index
C = sgn (q · ∇k ω)
C+ − C−
C+ + C−
(1)
measures the dichroism strength, with C = 0 corresponding to no dichroism and C = ±1 to
maximal dichroism. A mode with C > 0.5 and C < −0.5 is called right-circularly-polarized
(RCP) and left-circularly-polarized (LCP), respectively. The coupling index
β=
C+ + C−
2
(2)
is twice the average ability of an incident plane wave of arbitrary polarization to couple with a
crystal mode. A mode is called low coupling if β < 0.1.
We specifically address circular dichroism in two C(Y) photonic crystal geometries, of symmetry I41 32, for light incident along the [100] axes: Fig. 3 shows the results for the photonic
crystal consisting of two dielectric network domains, made of silicon, bounded by CMC surfaces and separated by a vacuum matrix domain. For k along [100] a partial band gap is observed
between [ω1 , ω2 ] := {ω|ω1 < ωa/(2πc) < ω2 }, that is a frequency range without any bands
regardless of polarization. This observation agrees with the observed full reflectance (R ≈ 1).
8
Further, a RCP circular dichroism band gap of width ∆ ≈ 9% is observed for [ω3 , ω4 ], that is a
frequency band for which only a LCP band (with sufficiently high coupling coefficient β) exists
but no RCP band; this explains the almost complete reflection of RCP incident light (R ≈ 1)
and the low reflectance of LCP light (R ≈ 0). A less clearly resolved feature of the photonic
band structure is the existence of another circular dichroism band gap of opposite polarization,
LCP, for [ω5 , ω6 ]. In line with lower values of β, the correspondence between the band structure
analysis and the scattering matrix results for R is more ambiguous. This chiral photonic crystal
can act as a circular polarization switch, for which the range of reflected colors depends on the
circular polarization of the incident white light, being [ω3 , ω4 ] for RCP and [ω5 , ω6 ] for LCP
light.
Fig. 3 shows the band structure of the photonic crystal geometry with a silicon sheet of
constant thickness bounded by parallel surfaces at distance ±r0 that is draped onto the C(Y)
minimal surface and that separates two vacuum network domains; the silicon filling fraction
is Φ = 46.7% corresponding to r0 = 0.05 a (a is the cubic lattice parameter). Topologically,
it represents the complement of the structure discussed above, with geometric differences due
to the type of bounding surface and the different filling fraction. The principal result of this
analysis is that neither the band structure nor the reflectance rates show any substantial amount
of circular dichroism even though the spatial structure is chiral with clearly handed local spiral
elements. This results is valid for other filling fractions as well. The partial band gap in the
frequency regions [ω1 , ω2 ], [ω3 , ω4 ] and above ω5 , where only low coupling modes exist, correspond to high reflectivity R.
In some regions, strong circular dichroism C of opposite handedness for a pair of bands is
found, e.g. below ω1 . However, the modes of these two bands are almost degenerate, explaining
9
C
β
|k|
R
0.8
ω5
0.7
ω4
0.6
ωa/2πc
ω3
0.5
ω2
ω1
0.4
RCP
LCP
0.3
-0.8 -0.4
0
0.4 0.8 Γ
X
0.2
0.6
10
0.5
1
Figure 3: Polarization analysis for a thickened C(Y) minimal surface made of silicon as shown
in Fig. 1. The dielectric is bounded symmetrically by parallel sheets on both sides of the minimal surface so that the volume fraction is φ = 46.7%. See fig. 2 for a description of the axes.
why no circular dichroism is observed in the reflectance spectrum. There is no single polarization sense, which couples significantly better to the chiral crystal structure than the opposite
sense. It is puzzling that for the equivalent structure bounded by CMC surfaces (i.e. same space
group with same screw axes, same topology and volume fraction), stronger interaction with the
dielectric and hence a larger energy split of the two corresponding bands is found (not shown).
A closer inspection of the eigenfields, however, may answer the question of geometrical relevance for circular dichroism.
10
3 Conclusions
We have introduced photonic crystal designs based on the chiral and cubic triply-periodic C(Y)
minimal surface as an alternative to conventional chiral photonic geometries based on chiral
line stackings or arrangements of spiral elements. We have shown that a photonic crystal consisting in two intertwined silicon network domains given by the two C(Y) skeletal graphs has
a partial band gap along the [100] direction as well as two circular dichroism gaps of different
polarization; this results in different colour of the reflection of incident white light depending
on the polarization. Further, a silicon sheet of constant thickness draped onto the C(Y) minimal
surface is an example for a photonic crystal geometry which shows almost no circular dichroism
despite having a chiral spatial structure with local chiral elements.
Further minimal surfaces of cubic symmetry that are chiral in their uncolored and their colored space groups are include the “C(Y)b” [19], the “D2c” and the “Yb” surfaces [8]. Chiral
sheet-like versions of the Gyroid minimal surface, which is achiral in its uncolored symmetry
group Ia3d but chiral in the colored symmetry group, are possible by extruding the surface
sheet to one side of the surface only.
Our study constitutes a step towards a deeper understanding of the relevance of the different motifs or elements that can constitute a chiral geometry (such as single- or double-helices,
helicoid-like sheets, chiral stackings, etc.) for photonic properties. Chirality is often interpreted
locally whereas the screw transformations act on the global geometry. Whether or not both
global and local aspects are important is currently unclear. Similarly, the relative importance of
geometric detail (such as the differences between the parallel sheet, constant-mean-curvature
or tubular graph structures) and global structure (such as symmetry, topology or homotopy) for
11
photonic properties is an open question that can be addressed by the study of well-defined structures. We propose that periodic minimal surfaces and nets provide a useful structure resource to
resolve these intriguing questions, including the most fundamental one: Which chiral structure
elements give rise to circular dichroism and which ones do not?
The relationship between the photonic band structure of an infinite photonic crystal and the
transmission rates through a finite section is an only partially solved problem, even without the
added complication of explicit surface modes. Our current approach is to quantify the degree
of circular polarization of individual Bloch modes by overlap integrals with circularly polarized
plane waves. The results yield agreement with scattering matrix calculations for the reflectance
coefficients for frequency ranges with a sufficiently small number of bands; degenerate bands
may appear circularly polarized even though the resulting superposed field configuration is not.
This method may be improved by determining the Bloch mode coefficients of superposed solutions from conservation laws, such as Poynting’s Theorem for the time averaged fields. Further,
the simple overlap integrals that quantify the coupling coefficient β between a plane wave and
a given Bloch mode are coarse approximations to transition probabilities and may be improved
by ideas similar to those that lead to Fermi’s golden rule.
Finally, steady improvement of rapid prototyping methods, such as direct laser writing,
make fabrication of metamaterials based on surface geometries such as the C(Y) a likely prospect.
For such processes, mechanical stability is a further property to be considered in addition to
photonic properties, with sheet-like geometries possibly yielding stronger structures than those
based on tubular networks.
12
References
[1] J. Pendry, Science 306, 1353 (2004).
[2] J. Gansel, et al., Science 325, 1513 (2009).
[3] A. V. Rogacheva, V. A. Fedotov, A. S. Schwanecke, N. I. Zheludev, Phys. Rev. Lett. 97,
177401 (2006).
[4] V. Saranathan, et al., Proceedings of the National Academy of Sciences 107, 11676 (2010).
[5] G. Schröder, et al., to be published (2010).
[6] A. Schoen, Infinite periodic minimal surfaces without self-intersections, Tech. rep., NASA
(1970).
[7] H. Schwarz, Gesammelte Mathematische Abhandlungen. 2 Bände. (Springer, Berlin,
1890).
[8] E. Lord, A. Mackay, Curr. Sci. 85, 346 (2003).
[9] A. Fogden, S. Hyde A48, 575 (1992).
[10] A. Fogden, S. Hyde, Eur. Phys. J. B 7, 91 (1999).
[11] G. Schröder, S. Ramsden, A. Christy, S. Hyde, Eur. Phys. J. B 35, 551 (2003).
[12] G. Schröder, Skeletons in the labyrinth, Ph.D. thesis, Australian National University, Canberra, Australia (2005).
[13] T. Hahn, ed., International Tables For Crystallography (Kluwer Academic Publishers,
Dordrecht, 1992), third and revised edn.
13
[14] K. Grosse-Braukmann, Journal of Colloid and Interface Science 187, 418 (1997).
[15] K. Brakke, Experimental Mathematics 1, 141 (1992).
[16] D. M. Whittaker, I. S. Culshaw, Phys. Rev. B 60, 2610 (1999).
[17] J. Lee, C. T. Chan, Opt. Express 13, 8083 (2005).
[18] M. Saba, et al., in preparation (2010).
[19] W. Fischer, E. Koch, Phil. Trans.: Math., Phys. and Engin. Sc. 354, 2105 (1996).
14