Majid Naeimi - Deutsche Geodätische Kommission

Transcription

Deutsche Geodätische Kommission
der Bayerischen Akademie der Wissenschaften
Reihe C
Dissertationen
Heft Nr. 711
Majid Naeimi
Inversion of satellite gravity data
using spherical radial base functions
München 2013
Verlag der Bayerischen Akademie der Wissenschaften
in Kommission beim Verlag C. H. Beck
ISSN 0065-5325
ISBN 978-3-7696-5123-2
Diese Arbeit ist gleichzeitig veröffentlicht in:
Wissenschaftliche Arbeiten der Fachrichtung Geodäsie und Geoinformatik der Leibniz Universität Hannover
ISSN 0174-1454, Nr. 309, Hannover 2013
der Bayerischen Akademie der Wissenschaften
Reihe C
Dissertationen
Heft Nr. 711
Inversion of satellite gravity data
using spherical radial base functions
Von der Fakultät für Bauingenieurwesen und Geodäsie
der Gottfried Wilhelm Leibniz Universität Hannover
zur Erlangung des Grades
Doktor-Ingenieur (Dr.-Ing.)
genehmigte Dissertation
von
M.Sc. Majid Naeimi
München 2013
Verlag der Bayerischen Akademie der Wissenschaften
in Kommission bei der C. H. Beck'schen Verlagsbuchhandlung München
ISSN 0065-5325
ISBN 978-3-7696-5123-2
Diese Arbeit ist gleichzeitig veröffentlicht in:
Wissenschaftliche Arbeiten der Fachrichtung Geodäsie und Geoinformatik der Leibniz Universität Hannover
ISSN 0174-1454, Nr. 309, Hannover 2013
Adresse der Deutschen Geodätischen Kommission:
Alfons-Goppel-Straße 11 ! D – 80 539 München
Telefon +49 – 89 – 23 031 1113 ! Telefax +49 – 89 – 23 031 - 1283 / - 1100
e-mail hornik@dgfi.badw.de ! http://www.dgk.badw.de
Prüfungskommission
Referent:
Prof. Dr.-Ing. Jakob Flury
Korreferenten: Prof. Dr.-Ing. Michael Schmidt
PD Dr. Gerhard Heinzel
Prof. Dr.-Ing. Ingo Neumann
Tag der mündlichen Prüfung:
23.08.2013
© 2013 Deutsche Geodätische Kommission, München
Alle Rechte vorbehalten. Ohne Genehmigung der Herausgeber ist es auch nicht gestattet,
die Veröffentlichung oder Teile daraus auf photomechanischem Wege (Photokopie, Mikrokopie) zu vervielfältigen
ISSN 0065-5325
ISBN 978-3-7696-5123-2
iii
Summary
The regional gravity field modelling based on satellite data in spherical radial base functions (SRBF) is
investigated in this thesis. The SRBF have been recently used for the regional representation of the Earth’s
gravity field as an alternative to the global spherical harmonic analysis. The use of SRBF for the regional
gravity field modelling requires several choices to be made. The shape of the SRBF and their positions, the
treatment of boundary effects and the use of a prior gravity field model to reduce the long wavelengths can be
mentioned as different choices which have to be made. There is a wide variety of options for these choices
which make it almost impossible to define a unique and standard way for regional gravity field modelling.
Moreover, no matter how these choices are made, the resulting observation equations are strictly inconsistent
and the associated design and normal matrices are strongly ill-posed. The solution must be then obtained by
means of a proper regularization method. The main objective of this thesis is the development of new methods
for the regularization of regional gravity field solutions based on satellite data.
In the first three chapters of the thesis, the basic concepts of the satellite gravimetry and gradiometry are given
briefly. Several mathematical models for the functional link between satellite observations and the gravitational
potential are addressed. Furthermore, the mathematical expressions of the global gravity field modelling using
spherical harmonics and SRBF are given. It will be numerically shown that these two groups of base functions
provide the same accuracy for the representation of gravity field on the global scale. The spatial pattern of
the estimated scaling coefficients on the global scale (for the SRBF) gives a perspective about the expected
‘geometry’ of the coefficients (as unknown parameters) in the regional modelling. Such perspective can be
then used as prior knowledge about the unknown parameters.
In Chapter 4, the mathematical description of global gravity field modelling using SRBF, is extended to regional
solutions. We classify different choices for the model setup to seven groups. These groups are investigated in
detail and our approach to define the choices is proposed.
In Chapter 5, the issue of regularization of discrete ill-posed problems will be investigated generally. We
describe the mathematical description of the ill-posed problems in general. In addition, some ‘diagnostic’
tools to determine the extent of the ‘ill-posedness’ will be introduced. The Tikhonov regularization and the
singular value decomposition, as powerful tools for the treatment of ill-posed problems, are explained further.
Several techniques for the choice of (Tikhonov) regularization parameter such as the variance component
estimation (VCE), the generalized cross validation (GCV) and the L-curve method are considered. Based on
the space-localization properties of the SRBF, we introduce our proposed method, called the parameter-signal
correlation (PSC), for the choice of regularization parameter. Since the regularization parameter should be
chosen from an extremely large set of numbers, we also propose two methods to obtain an initial and realistic
value for the regularization parameter. These methods significantly reduce the computation costs and lead to a
very fast convergence. The connection between the regularization and the shape of SRBF will also be explained
which simplifies the choice of the shape functions.
Finally, the regional gravity field modelling will be numerically investigated in several test areas. We chose
three test regions according to their geographical locations as well as their signal contents. These regions
are: Scandinavia, Central Africa and South America along the Andes. In addition, we considered two types
of satellite observations: simulated GRACE-type data corrupted with coloured noise and real GOCE gravity
gradients. Therefore the numerical considerations are divided into two steps. In the first step, the simulated
GRACE data are considered. A global gravity field solution using spherical harmonics up to degree and order
120, as well as several regional solutions, are determined based on the same simulated satellite data. For the
regional solutions, the VCE, GCV, L-curve and the proposed PSC methods have been used as the regularization
iv
parameter choice methods. The results are then compared to the input model to quantify the quality of different
solutions. In all solutions, our PSC method gives the most promising results with the least geoid RMS on the
Earth’s surface. It also gives better results when the regional solutions are compared to the global spherical
harmonic solution in the corresponding regions. The north-south GRACE stripes are remarkably reduced
as the result of PSC regularization. In the second step, we employed real GOCE observations for regional
modelling. Two months of calibrated Vzz components are used. The solutions are compared to the global
gravity field model EGM2008 as well as the recent combined model GOCO03s. Again, the performance of four
different regularization approaches are compared in the test areas. The PSC method gives the least geoid RMS
compared to other approaches which shows the success of the proposed method. Moreover, the solutions show
a considerable improvement compared to the global model EGM2008. The deviations between the regional
solutions and the model GOCO03s, are also in the range of accumulated geoid errors of the recent global
models. This indicates that even a short period of GOCE observations can provide promising results in medium
and short wavelengths of the Earth’s gravity field. In addition, this provides evidence that the regional gravity
field determination based on satellite data provides satisfactory results if the solution is properly regularized.
v
Zusammenfassung
In der vorliegenden Arbeit wird ein Ansatz zur regionalen Schwerefeldmodellierung mit sphärischen
radialen Basisfunktionen (SRBF) untersucht. Sphärische radiale Basisfunktionen werden seit wenigen
Jahren für die regionale Darstellung des Erdschwerefeldes genutzt und stellen eine Alternative zur
globalen sphärisch-harmonischen Analyse dar. Beim Einsatz radialer Basisfunktionen für die regionale
Schwerefeldmodellierung sind verschiedene Entscheidungen zu treffen. Es seien beispielhaft die Wahl der
Form der sphärischen radialen Basisfunktion und deren Position, die Behandlung von Randeffekten sowie die
Verwendung eines bereits existierenden Schwerefeldmodells zur Reduktion langwelliger Schwerefeldanteile
genannt. Die Vielfalt an denkbaren Optionen (für diese Entscheidungen) macht es beinahe unmöglich, ein
Standardverfahren für die regionale Schwerefeldmodellierung zu definieren. Darüber hinaus sind unabhängig
von den getroffenen Entscheidungen die sich ergebenden Beobachtungsgleichungen streng inkonsistent, was
zu einem schlecht gestellten inversen Problem führt. Die Lösung muss dann mit Hilfe eines geeigneten
Regularisierungsverfahrens erreicht werden. Das Hauptziel dieser Arbeit ist die Entwicklung neuer Methoden
zur Regularisierung regionaler Schwerefeldlösungen basierend auf Satellitendaten.
In den ersten drei Kapiteln, werden in Kürze die grundlegenden Konzepte der Satellitengravimetrie und
Satellitengradiometrie erläutert und mehrere mathematische Modelle für die funktionalen Zusammenhänge
zwischen Satellitenbeobachtungen und Gravitationspotential dargestellt. Ferner werden die mathematischen
Modelle der globalen Schwerefeldmodellierung sowohl in Form sphärisch-harmonischer als auch
sphärisch-radialer Basisfunktionen beschrieben. Es wird numerisch belegt, dass diese beiden Gruppen
von Basisfunktionen für die Darstellung von Schwerefeldmodellen auf einer globalen Skala die gleichen
Genauigkeiten aufweisen. Das räumliche Muster der geschätzten Skalierungskoeffizienten (für die sphärischen
radialen Basisfunktionen) auf einer globalen Skala gibt Aufschluss über die zu erwartende Geometrie der
Koeffizienten (als unbekannte Parameter) in der regionalen Modellierung. Aus derartigen Betrachtungen
können Vorabinformationen über die unbekannten Parameter abgeleitet werden.
In Kapitel 4 wird die mathematische Beschreibung globaler Schwerefeldmodellierung unter Einsatz von SRBF
auf regionale Lösungen erweitert. Es erfolgt eine Klassifizierung verschiedener Optionen des Modells in bis zu
sieben Gruppen. Diese Gruppen werden detailliert untersucht und es wird ein Ansatz für die Wahl der Optionen
vorgeschlagen.
Kapital 5 stellt den Hauptteil der Arbeit dar und geht allgemein auf das Thema der Regularisierung von
diskreten schlecht gestellten Problemen und deren mathematische Beschreibung ein. Es wird ein Diagnose-Tool
vorgestellt, welches die Bestimmung des Ausmaßes eines schlecht gestellten Problems ermöglicht. Ergänzend
werden die Tikhonov Regularisierung und Singulärwertzerlegung als zwei leistungsfähige Verfahren zur
Behandlung schlecht gestellter Probleme erläutert. Es werden verschiedene Techniken für die Wahl des
(Tikhonov) Regularisierungsparameter betrachtet, wie etwa die Varianzkomponentenschätzung (VCE), die
generalisierte Kreuzvalidierung (GCV) und die L-curve Methode.
Basierend auf den raum-lokalisierenden Eigenschaften der sphärischen radialen Basisfunktionen wird die
im Rahmen dieser Arbeit vorgeschlagene Methode, die sogenannte Parameter-Signal Korrelation (PSC),
zur Wahl der Regularisierungsparameter vorgestellt. Da die Regularisierungsparameter aus einer extrem
großen Menge an Zahlen gewählt werden sollten, werden ebenfalls zwei Methoden vorgeschlagen, um
einen initialen und einen realistischen Wert für die Regularisierungsparameter zu erhalten. Diese Methoden
tragen zu einer deutlichen Verringerung der Rechenzeit sowie zu einer sehr schnellen Konvergenz bei.
Die Verbindung zwischen der Regularisierung und der Form der sphärischen radialen Basisfunktion
wird ebenfalls erläutert, wodurch die Wahl der Formfunktion vereinfacht wird. Schließlich wird die
vi
regionale Schwerefeldmodellierung in mehreren Testgebieten numerisch untersucht. Die Auswahl fiel
auf drei Testgebiete, die anhand ihrer geografischen Lage sowie ihres Signalgehalts ausgewählt wurden.
Die Gebiete sind Skandinavien, Zentralafrika und Südamerika entlang der Anden. Als zwei Arten
von Satellitenbeobachtungen werden simulierte GRACE-Daten mit farbigem Rauschen und reale GOCE
Gravitationsgradienten genutzt. Die numerischen Betrachtungen werden in zwei Schritte unterteilt. Im ersten
Schritt werden die simulierten GRACE-Daten berücksichtigt. Daraus wird eine globale Schwerefeldlösung
in Form von sphärisch-harmonischen Koeffizienten bis Grad und Ordnung 120 sowie mehrere regionale
Lösungen auf Basis derselben Satellitendaten bestimmt. Für die regionalen Lösungen werden für die Wahl
der Regularisierungsparameter die VCE, GCV, L-curve und die vorgeschlagene PSC Methode verwendet.
Die Ergebnisse werden dann mit dem Eingangsmodell verglichen, um die Qualität verschiedener Lösungen
zu quantifizieren. In allen Lösungen liefert das PSC Verfahren die vielversprechendsten Ergebnisse mit dem
geringsten Geoid RMS Fehler auf der Erdoberfläche. Das Verfahren führt ebenfalls zu den besten Ergebnissen,
wenn die regionalen Lösungen in den entsprechenden Gebieten mit den globalen sphärisch-harmonischen
Lösungen verglichen werden. Die GRACE Streifen in Nord-Süd-Richtung werden als ein Resultat der PSC
Regularisierung erheblich reduziert. Im zweiten Schritt werden reale GOCE Beobachtungen in Form von zwei
Monaten kalibrierter Vzz Tensorkomponenten für die regionale Modellierung genutzt. Die Ergebnisse werden
einerseits mit dem globalen Schwerefeldmodell EGM2008 sowie dem rein satellitenbasieren Kombinationsmodell GOCO03s verglichen. Erneut werden in den Testgebieten die Ergebnisse der vier Regularisierungsansätze miteinander verglichen. Die PSC Methode liefert den geringsten Geoid RMS im Verglich zu den
anderen Ansätzen, was die Überlegenheit der vorgeschlagenen Methode unterstreicht. Darüber hinaus zeigt
die Lösung eine erhebliche Verbesserung gegenüber dem globalen Modell EGM2008. Die Abweichungen
zwischen den regionalen Lösungen und dem Modell GOCO03s liegen im Bereich der akkumulierten Geoidfehlergradvarianzen der neuesten globalen Modelle. Dies deutet darauf hin, dass bereits ein kurzer Zeitraum
von GOCE Beobachtungen vielversprechende Ergebnisse im Bereich mittlerer und kurzer Wellenlängen des
Erdschwererfeldes liefern kann. Außerdem stellt dies auch den Beweis dar, dass eine regionale Schwerefeldbestimmung auf Basis von Satellitendaten zufriedenstellende Ergebnisse liefert, wenn die Lösung geeignet
regularisiert wird.
vii
Abbreviations
CHAMP
CuP
GCV
GFZ
GOCE
GPS
GRACE
GRF
KBR
LEO
LNOF
PSC
RMS
SGG
SH
SRBF
SST
SST-hl
SST-ll
SVD
VCE
CHAllenging Mini-satellite Payload
Cubic Polynomials
Generalized Cross Validation
GeoForschungsZentrum (German Research Centre for Geosciences)
Gravity and steady-state Ocean Circulation Explorer
Global Positioning System
Gravity Recovery And Climate Experiment
Gradiometer Reference Frame
k-Band Ranging
Low Earth Orbiter
Local North Oriented Frame
Parameter-Signal-Correlation
Root Mean Square
Satellite Gravity Gradiometry
Spherical Harmonics
Spherical Radial Base Function
Satellite-to-Satellite Tracking
Satellite-to-Satellite tracking, high-low
Satellite-to-Satellite tracking, low-low
Singular Value Decomposition
Variance Component Estimation
Contents
ix
Contents
1 Introduction
1.1 Problem statement and thesis objectives . . . . . . . . . . . .
1.2 Thesis outlines . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Preliminaries . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3.1 Units and constants . . . . . . . . . . . . . . . . . . .
1.3.2 Components of the Earth’s gravity field . . . . . . . .
1.3.3 Functionals and observables of the Earth’s gravity field
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
3
4
4
4
5
5
2 Gravity field from satellite data
2.1 Precise orbit determination . . . . . . . . . . . . . . . . . . . . . .
2.2 Gravity field from SST data . . . . . . . . . . . . . . . . . . . . . .
2.2.1 Variational approach . . . . . . . . . . . . . . . . . . . . .
2.2.2 Short arc approach . . . . . . . . . . . . . . . . . . . . . .
2.2.3 Acceleration approach . . . . . . . . . . . . . . . . . . . .
2.2.4 Energy balance approach . . . . . . . . . . . . . . . . . . .
2.3 Gravity field from SGG data . . . . . . . . . . . . . . . . . . . . .
2.3.1 Gravity gradiometry . . . . . . . . . . . . . . . . . . . . .
2.3.2 From the GOCE observation frame to the Earth fixed frame
2.4 Evolution of global gravity field models and state-of-the-art . . . . .
2.5 Follow-on missions . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
9
9
11
11
12
13
15
16
16
18
19
.
.
.
.
.
.
.
.
.
.
.
.
3 Global gravity field modelling
3.1 Spherical harmonics (SH) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.1 Mathematical description of SH . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2 Expansion of the gravitational potential into SH . . . . . . . . . . . . . . . .
3.1.3 Estimation of spherical harmonic coefficients using least-squares adjustment
3.1.4 Disadvantages of spherical harmonics . . . . . . . . . . . . . . . . . . . . .
3.2 Spherical radial base functions (SRBF): A first look . . . . . . . . . . . . . . . . . .
3.2.1 Mathematical description of SRBF . . . . . . . . . . . . . . . . . . . . . . .
3.2.2 Relation to spherical harmonics . . . . . . . . . . . . . . . . . . . . . . . .
3.3 SH versus SRBF in satellite gravimetry: numerical aspects on the global scale . . . .
3.3.1 Simulated input data and noise . . . . . . . . . . . . . . . . . . . . . . . . .
3.3.2 Global gravity field solutions . . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
23
24
24
27
29
31
32
33
35
35
36
37
4 Regional gravity field modelling using SRBF
4.1 From global to regional scale . . . . . . . . . .
4.2 Model setup using SRBF . . . . . . . . . . . .
4.2.1 Shape of the SRBF . . . . . . . . . . .
4.2.2 Maximum degree of expansion . . . . .
4.2.3 Removal of the long wavelengths . . .
4.2.4 Position of the SRBF . . . . . . . . . .
4.2.5 Extension of the data zone . . . . . . .
4.2.6 Extension of the grid zone . . . . . . .
4.2.7 Inversion process . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
41
41
43
44
48
49
50
53
54
55
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
x
Contents
5 Regularization of regional gravity field solutions
5.1 Gravity field modelling: an inverse problem . . . . . . . . . . . . . . . .
5.2 Diagnosis of ill-posedness in inverse problems . . . . . . . . . . . . . . .
5.2.1 Condition number . . . . . . . . . . . . . . . . . . . . . . . . .
5.2.2 Singular value decomposition . . . . . . . . . . . . . . . . . . .
5.2.3 Discrete Picard condition . . . . . . . . . . . . . . . . . . . . . .
5.3 Ill-posedness of gravity field determination . . . . . . . . . . . . . . . .
5.4 Regularization of ill-posed problems . . . . . . . . . . . . . . . . . . . .
5.4.1 Truncated singular value decomposition . . . . . . . . . . . . . .
5.4.2 Tikhonov regularization . . . . . . . . . . . . . . . . . . . . . .
5.4.3 Tikhonov regularization in terms of SVD . . . . . . . . . . . . .
5.5 The choice of the regularization parameter . . . . . . . . . . . . . . . . .
5.5.1 Generalized cross validation . . . . . . . . . . . . . . . . . . . .
5.5.2 Variance component estimation . . . . . . . . . . . . . . . . . .
5.5.3 L-curve analysis . . . . . . . . . . . . . . . . . . . . . . . . . .
5.6 Signal-adaptive parameter choice: The parameter-signal correlation (PSC)
5.7 Initial value for the regularization parameter . . . . . . . . . . . . . . . .
5.7.1 Initial guess based on the size of the region . . . . . . . . . . . .
5.7.2 Initial guess based on the condition number . . . . . . . . . . . .
5.8 Different types of SRBF and their impact on the regularization . . . . . .
5.9 Assessment of regional solutions . . . . . . . . . . . . . . . . . . . . . .
5.9.1 Statistical assessment . . . . . . . . . . . . . . . . . . . . . . . .
5.9.2 External validation . . . . . . . . . . . . . . . . . . . . . . . . .
5.9.3 Model-dependent evidences . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
57
59
60
60
63
63
64
65
66
68
71
71
73
74
75
78
79
80
81
83
83
84
84
6 Numerical results
6.1 Specifications of regional solutions . . . . . . . . . . . . . . . . .
6.1.1 Test regions . . . . . . . . . . . . . . . . . . . . . . . . .
6.1.2 Type of SRBF . . . . . . . . . . . . . . . . . . . . . . .
6.1.3 Type of grid points . . . . . . . . . . . . . . . . . . . . .
6.2 Regional gravity field modelling based on GRACE-type simulation
6.2.1 Simulated data and noise . . . . . . . . . . . . . . . . . .
6.2.2 Regional solutions in Central Africa . . . . . . . . . . . .
6.2.3 Regional solutions in Scandinavia . . . . . . . . . . . . .
6.2.4 Regional solutions in South America . . . . . . . . . . .
6.3 Regional gravity field modelling based on GOCE gravity gradients
6.3.1 GOCE data and functional model . . . . . . . . . . . . .
6.3.2 Setting up the regional models . . . . . . . . . . . . . . .
6.3.3 Regional solutions based on GOCE data . . . . . . . . . .
6.3.4 Summary of regional solutions based on real GOCE data .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
85
85
85
86
86
87
87
88
95
99
104
104
106
106
117
7 Summary and conclusions
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
119
List of Figures
xi
List of Figures
1.1
1.2
1.3
The approximate value of the global gravity . . . . . . . . . . . . . . . . . . . . . . . . . . .
The value of gravity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The long term gravity changes on the global scale . . . . . . . . . . . . . . . . . . . . . . . .
2.1
2.2
2.3
2.4
2.5
2.6
The Earth’s gravity field from different satellite techniques
Concept of SST high-low and SST low-low . . . . . . . .
Coordinate systems used for GOCE data processing . . . .
Satellite missions and spatial resolution . . . . . . . . . .
Error degree amplitudes in terms of geoid heights . . . . .
Cumulative geoid errors for several global models . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
8
10
17
20
21
22
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
Normalized spherical harmonics of degree 4 . . . . . . . . . . . . . . . . . . . . . . . . .
Uncertainty principle in space and frequency . . . . . . . . . . . . . . . . . . . . . . . .
SRBF of different resolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Geoid heights computed from geopotential model GOCO03s up to Nmax = 70 . . . . . .
geoid error degree amplitude of the global model . . . . . . . . . . . . . . . . . . . . . .
Geoid differences between the global model GOCO03s and the computed model using SH
Similarity of the geoid heights and the estimated coefficients . . . . . . . . . . . . . . . .
Cross-correlation function for the estimated scaling coefficients αk and the geoid heights .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
32
34
36
38
39
40
40
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
4.10
Gravity field modelling on global and regional scales . . . . . . . . . .
Model zone, data zone and grid zone . . . . . . . . . . . . . . . . . . .
The Shannon kernel . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The Blackman kernel . . . . . . . . . . . . . . . . . . . . . . . . . . .
The CuP kernel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The spline kernel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Distance between adjacent SRBF on the Reuter grid . . . . . . . . . . .
Two Reuter grids with different point densities . . . . . . . . . . . . . .
The Reuter and Fibonacci grids . . . . . . . . . . . . . . . . . . . . . .
The extension of the grid and data zones with respect to the model zone
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
41
43
45
46
47
48
52
52
53
54
5.1
5.2
5.3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.11
5.12
The forward and inverse problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The operator A and its mapping from function space to the observation space . . . . . .
Two coordinate systems to describe one object . . . . . . . . . . . . . . . . . . . . . . .
Singular values of the normal matrices on global and regional scales . . . . . . . . . . .
Non-regularized and regularized coefficients . . . . . . . . . . . . . . . . . . . . . . . .
Singular values, regularization and filter factors . . . . . . . . . . . . . . . . . . . . . .
The generalized cross validation function . . . . . . . . . . . . . . . . . . . . . . . . .
The L-curve and its curvature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The PSC function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
The geoid difference for the models EGM2008 and EGM1996 used for the PSC method
The search band for the choice of regularization parameter . . . . . . . . . . . . . . . .
The sequence of matrix operations to obtain the solution from the observation vector . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
57
58
62
64
68
70
72
74
77
78
79
83
6.1
6.2
Test areas for regional gravity field modelling . . . . . . . . . . . . . . . . . . . . . . . . . .
Simulation scenario used to assess the performance of regional gravity field modelling . . . .
86
87
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
2
2
xii
List of Figures
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.20
6.21
6.22
6.23
6.24
6.25
The geoid differences between the estimated global model using SH and the model GOCO03s
88
geoid and geoid differences in Central Africa . . . . . . . . . . . . . . . . . . . . . . . . . . 89
The model zone ,the data zone and the grid zone in Central Africa . . . . . . . . . . . . . . . 90
The coefficients obtained from the PSC regularization approach in Central Africa . . . . . . . 92
The geoid differences between the model GOCO03s and regional solutions in Central Africa
(Reuter) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
The geoid differences between the model GOCO03s and regional solutions in Central Africa
(Fibonacci) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94
Geoid and geoid differences in Scandinavia . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
The model zone, the data zone and the grid zone for regional modelling in Scandinavia . . . . 96
The geoid differences between the model GOCO03s and the regional solutions in Scandinavia
97
The coefficients obtained from the PSC regularization approach in Scandinavia . . . . . . . . 98
Geoid and geoid differences in the are of Andes . . . . . . . . . . . . . . . . . . . . . . . . . 99
The model, data and grid zones for regional modelling in the Andes . . . . . . . . . . . . . . 100
The estimated coefficients obtained from the PSC regularization approach in South America . 101
The geoid differences between the model GOCO03s and the regional solutions in South America102
The differences between regional solutions in Central Africa and the global model EGM2008 . 108
The differences between regional solutions in Central Africa and the global model GOCO03s . 109
The estimated coefficients and geoid heights in Central Africa . . . . . . . . . . . . . . . . . 110
The differences between regional solutions in Scandinavia and the global model EGM2008 . . 112
The differences between regional solutions in Scandinavia and the global model GOCO03s . . 113
The estimated coefficients and geoid heights in Scandinavia . . . . . . . . . . . . . . . . . . . 114
The differences between regional solutions in the Andes and the global model EGM2008 . . . 116
The differences between regional solutions in the Andes and the global model GOCO03s . . . 116
The estimated coefficients and geoid heights in the area of Andes . . . . . . . . . . . . . . . . 117
List of Tables
xiii
List of Tables
1.1
Table of constants . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1
2.2
Several past and current dedicated satellite missions . . . . . . . . . . . . . . . . . . . . . . .
Several geopotential models determined from 1999 until 2013 . . . . . . . . . . . . . . . . .
7
19
5.1
Different geopotential models used to compute dVk for the PSC method . . . . . . . . . . . .
78
6.1
6.2
6.3
6.4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.12
6.13
Specifications of the regional modelling in Central Africa . . . . . . . . . . . . .
Summary of the regional solutions in Central Africa and their quality measures .
Summary of the solutions in Central Africa and their quality measures . . . . . .
Specifications of the regional modelling in Scandinavia . . . . . . . . . . . . . .
Summary of the regional solutions in Scandinavia with their quality measures . .
Specifications of the regional modelling in South America along the Andes . . .
Summary of the regional solutions in the Andes with their quality measures . . .
Specifications of the regional modelling in Central Africa . . . . . . . . . . . . .
Summary of the regional solutions in Central Africa and their quality measures .
Specifications of the regional modelling in Scandinavia . . . . . . . . . . . . . .
Summary of the regional solutions in Scandinavia and their quality measures . .
Specifications of the regional modelling in the area of the Andes . . . . . . . . .
Summary of the regional solutions in the area of Andes and their quality measures
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
91
93
94
96
97
100
102
107
107
111
111
115
115
1
1 Introduction
Gravity is the well-known force near the Earth’s surface which directly influences many aspects of humankind’s
life. As a physical property of the Earth, the gravity is a function of mass distribution and mass redistribution.
The Earth’s geometry, on the other hand, is also dependent on the mass structure of the Earth. Therefore, gravity
is a way to connect the geometry of the Earth to its physical properties and it plays an important role in the
definition of the figure of the Earth. The approximate value of gravity acceleration, near the Earth’s surface, is
about 9.8 m/s2 which multiplied by the mass of particles, determines the force of gravity. Due to its dependency
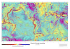
on the mass distribution (and redistribution), gravity varies in space and in time. Figure 1.1 illustrates the value
of gravity near the Earth’s surface.
Figure 1.1: The approximate value of the gravity acceleration at the Earth’s surface. The maximum values are
in polar regions while the minima are in the equatorial area. For a better visualization the anomalies
are exaggerated.
As it can be seen in figure 1.1, the global variations of the gravity range from about 9.75 to 9.85 m/s2 which is
mainly due to the Earth’s oblateness. This is the largest spatial variation on the Earth’s surface. Spatial changes
in smaller scales are due to regional and local properties of the Earth’s mass structure and mass changes. This
is symbolically shown in figure 1.2.
Temporal variations are caused by mass changes within the Earth system. Such mass changes can occur very
slowly over long periods of time (such as geological changes) or very sudden such as changes caused by
earthquakes and volcanic eruptions. Generally speaking, all phenomena, which are dependent on the mass
structure of the Earth or its variations, affect the gravity of the Earth. Figure 1.3 shows the secular changes
of the gravity on the global scale. The figure clearly shows that in some regions the gravity changes are
considerably large. For instance, in Greenland and Antarctic the gravity is decreasing as a result of ice mass
loss. In contrast, the gravity is increasing in Scandinavia due to the post glacial rebound in this region. Therefore
the precise knowledge of the Earth’s gravity field and its spatial and temporal variations is an important source
of information in determining the mass dependence of geophysical phenomena.
2
1 Introduction
Figure 1.2: The value of gravity and its dependency on different spatial and temporal mass changes inside the
Earth. The number 9 never changes near the Earth’s surface. The first two or three decimal numbers
(in the order of 10−2 m/s2 change only on the global scale. The changes in the range of 10−5 m/s2
are due to the heights in the continental scales. Finally the changes in the order of 10−8 m/s2 are
because of small scale changes in mass densities as well as temporal variations.
Hence, gravity observations are among the most fundamental data sets in geophysical and geodynamical studies
from global to local scales. Geological phenomena such as volcanic activities, tectonic plates, land uplift
and subsidence, interpreted as the mass movements in the Earth’s interior, can be monitored using gravity
observations. Hydrologists are also able to track water cycles in continents as well as water exchange between
land and ocean using gravity data. Studying the annual cycle of the snow pack, post glacial rebound (PGR) and
changes in sea-level are also possible using precise knowledge of the Earth’s gravitational field.
Figure 1.3: The long term gravity changes on the global scale. The results are based on the data from the
GRACE mission. In Greenland and Antarctica, gravity is decreasing because of ice mass loss. The
land uplift in Scandinavia and north America as the result of post glacial rebound, causes gravity
increase. The figure shows the annual rate of gravity changes.
In addition, almost all geodetic observations are affected by the gravity field of the Earth which should be
accounted for in data reduction steps (Vanicek and Krakiwsky, 1982). Accurate gravity field models are also
necessary for the orbit determination in satellite missions. There is a huge number of examples which state that
the precise knowledge of the Earth’s gravity field is essential in nearly all fields of the geosciences.
1.1 Problem statement and thesis objectives
3
1.1 Problem statement and thesis objectives
The modelling of the Earth’s gravity field is an old issue in geodesy and geophysics. High resolution gravity
field determination in the last decades was restricted to specific regions based on the available terrestrial
gravimetric data. The global recovery of the gravity field has only been possible since satellites were launched
in the 60’s. However due to the lack of high precision and high sensitive sensors on board satellites, the recovery
of global gravity fields was limited to the long wavelengths of the gravitational field.
Nowadays, thanks to the availability of a huge amount of data from current satellite missions, with highly
sensitive sensors, the recovery of detailed gravity field on the global scale is possible down to the spatial scales
of a few hundred kilometres. Since the year 2000, over 60 global gravity field models have been determined
using spherical harmonics based on either the combination of terrestrial and satellite data or satellite data
only (GFZ, 2013). Some of these models incorporate the same data sets but still have different characteristics.
Such diversity of existing global gravity field models indicates that the optimum gravity field determination
is a challenge and there is still room for further improvements. The main reason for the differences between
existing global models is due to the application of various mathematical approaches used to set up the models.
The mathematical approach includes the pre-processing of the data, the setup of the observation equations, the
base functions used for the representation, the weighting strategy for the noisy data, the matter of the inversion
and regularization and finally, the quality assessment of the solution.
Besides the global gravity field solutions, the issue of regional gravity field determination based on satellite
data manifolds the variety of options for gravity field determination. As an advantage of regional modelling,
the computational costs are significantly reduced, when the solution is confined to a region for a specific
application. But the main focus of the regional gravity field modelling is to extract more information out
of the data by passing the data through dedicated regional filters rather than global ones. This is possible by
employing a set of space-localizing base functions to zoom-in on the target region. Gravity field modelling
using space-localizing base functions has been investigated for several decades. The use of point masses as
an alternative to spherical harmonics can be mentioned as one of the early attempts to use space-localizing
base functions for the representation of the Earth’s gravity field (Weightman, 1965). Least-squares collocation
(Moritz, 1980) is another example of using space-localizing base function for regional gravity field modelling
in which the auto-covariance function is used as the analysing base function.
In the last two decades, regional gravity field modelling has been investigated by many research groups.
The reason is the availability of numerous and new sets of satellite-based observations. The mathematical
investigations at University of Kaiserslautern to develop the concept of multi-scale modelling using spherical
radial base functions (SRBF) and spherical wavelets (Freeden, 1999), the recent studies at University of Bonn
to use harmonic splines (Eicker, 2008), the multi-scale approach of the DGFI in Munich (Schmidt et al., 2007)
and the current focus of several research studies at Universities of Delft (Wittwer, 2009) and Stuttgart (Antoni,
2012) indicate more interest and demands for this issue. A more comprehensive overview of the previous works
in this field, will be given in section 4.2 where more details are addressed.
Despite the existence of several valuable research studies to determine the Earth’s gravity field on the regional
scales there is yet no standard and unique way to establish the regional modelling of the gravity using SRBF.
The reason originates in the fact that there are many choices and options in the construction of regional gravity
field models. Various types of space-localizing base functions, the position of the base functions, treatment of
border distortions and the inversion of the resulting ill-posed model can be mentioned for instance. Almost in
all previous works, the choices have been made using trial and error.
The goal of this PhD thesis is to develop a simple and efficient methodology for the regional gravity field
determination. We try to provide a reasonable strategy to put various components of regional gravity field
modelling together in a logical way. Thus, no extemporary choice shall be made in our methodology. The
emphasis is put on the satellite data but the method can be generalized to other types of observations as well.
In addition, we focus particularly on the inversion process where the solution must be obtained by means of a
proper regularization method.
4
1 Introduction
1.2 Thesis outlines
This PhD thesis is organized in seven chapters. In the remaining part of chapter 1, the basic definitions in the
context of the Earth’s gravity field are given. Section 2 is dedicated to the gravity field determination from
satellite data. A brief history of the gravity satellite missions is given. The precise orbit determination as
an important step in gravity field recovery will be shortly discussed. Moreover, several approaches for the
functional link between GRACE-type SST (Satellite-to-Satellite Tracking) data and the gravitational potential
are summarized. Furthermore, the functional model to determine the Earth’s gravity field based on the GOCE
gravity gradients as well as related problems will be considered. The section ends with the consideration of the
state-of-the-art and current developments in global gravity field modelling based on satellite data.
The representation of the global gravity field on the Earth’s surface will be investigated in chapter 3. First
the mathematical description of spherical harmonics as well as SRBF are given in detail. The least-squares
adjustment to determine the unknown coefficients will be addressed as well. As an alternative to spherical
harmonics, the applicability of SRBF to represent the gravity field on the global scale is considered. Although
it is not common to use the SRBF for the global modelling of the gravity field (due to its high computational
burden compared to spherical harmonics), such practice gives an insight into the regularization of regional
solutions using these base functions.
Section 4 addresses the regional modelling of the gravity using the SRBF. Due to the diversity of options for
the regional setup, a collection of choices has to be made to end up with the observation equations. We discuss
these choices and propose our methodology for the regional model setup.
Once the model is set up, the resulting observation equations are strongly inconsistent and the associated design
and normal matrices are strongly ill-posed. A useful solution should be then obtained by means of a proper
regularization method. This is a crucial issue in regional gravity field determination which must be taken into
account considerately. The regularization procedure of the ill-posed problems will be generally investigated in
chapter 5. The emphasis is put on the standard Tikhonov regularization where the choice of the regularization
parameter is the key issue. We address several well-known approaches for the choice of the regularization
parameter and discuss their characteristics. A new approach, called the parameter-signal-correlation (PSC), will
be proposed for the choice of the regularization parameter. The PSC method is dedicated to the regularization
of ill-posed problems where the SRBF serve as the analysing (base) functions.
In chapter 6, the performance of these regularization approaches will be studied in a comparison manner. To
check the methods under different conditions, the regional solutions will be determined in several test areas and
based on different types of satellite observations.
At the end, the summary and concluding remarks as well as further research directions in this field will be
provided in chapter 7.
1.3 Preliminaries
1.3.1 Units and constants
There are mainly two units used for the gravity: N/kg (Newton per kilogram) and m/s2 . The former is used in
analysis systems where the gravity, as a force, interacts with other forces. The latter, m/s2 , is widely used in
physics and geosciences, where gravity is considered as an acceleration. In geodesy and geophysics another
unit, gal, is also used for more detailed considerations. 1 gal is equal to 1 cm/s2 or 10−2 m/s2 . For some
applications mgal (milligal) and µgal (microgal) are used. The relations between these units are
1 N/kg = 1 m/s2 = 102 gal = 105 mgal = 108 µgal.
(1.1)
The unit used for the potential is m2/s2 . The second derivatives of the gravitational potential or gravity gradients,
have the dimension 1/s2 . Another unit used for the gravity gradients is Eötvös which is equal to 10−9/s2 .
In the context of the Earth’s gravity field modelling, several constants are used. These values might be slightly
different in various standards and models. We use the numerical values given by the International Earth Rotation
and Reference Systems Service (Petit and Luzum, 2010). Table 1 gives the value and the definition of these
constants which will be used in this thesis.
1.3 Preliminaries
Constant
G
GM
a
ωe
5
definition
value
dimension
universal gravitational constant
geocentric gravitational constant
semi major axis of rotational ellipsoid
the Earth’s angular velocity
6.67428 × 10−11
0.3986004418 × 1015
6.3781366 × 6
7.29211 × 10−5
m3/kgs2
m3/s2
m
rad/s
Table 1.1: The constants used in this thesis for gravity field determination. These values are given by the
international Earth Rotation and Reference Systems Service.
1.3.2 Components of the Earth’s gravity field
The gravity field of the Earth is composed of two parts:
• The gravitational part: this part is the consequence of all gravitational attractions within the Earth system
including its atmosphere. Gravitational acceleration gg at position i is a function of mass distribution and
mass densities inside the Earth and is given by Newton’s law of gravitation (e.g. Heiskanen and Moritz
(1967)):
ZZZ
ρ(r)
g
gi = GM
(r − ri )dV
(1.2)
kr − ri k3
V
in which ρ(r) is the density of the Earth as a function of the position vector r and dV is an infinitesimally
small element of the volume of the Earth V.
• The centrifugal part: this acceleration is caused by the Earth rotation and is computed using the Earth’s
angular velocity vector ω e and the distance pi from the Earth rotation axis:
gic = ω e × (ω e × pi ).
(1.3)
The maximum value of the centrifugal acceleration is on the equator and is approximately equal to
3.4 × 10−2 m/s2 . There is consequently no centrifugal acceleration at poles since pi = 0 .
The sum of these two accelerations is called the gravity g:
g = gg + gc .
(1.4)
In this thesis, the gravitational acceleration shall be considered. We use the terms gravitational acceleration and
gravity alternatively but unless otherwise stated, we mean the gravitational acceleration part.
1.3.3 Functionals and observables of the Earth’s gravity field
The vector of gravity is the gradient of a scalar field which is the gravitational potential. The gravitational
potential is denoted by V and is defined as:
∇V = g
(1.5)
T
in which ∇ = ∂/∂x ∂/∂y ∂/∂z is the gradient operator in an arbitrary three dimensional coordinate
system defined by the axes x, y and z. The main part of the gravitational potential can be described by the
potential of a reference ellipsoid approximating the figure of the Earth. This reference field is called the normal
potential and is denoted by U . The difference between the gravitational potential and the normal potential is
the disturbing potential T :
6
1 Introduction
T = V − U.
(1.6)
Similar to (1.5), the normal gravity is the gradient of the normal potential:
∇U = γ.
(1.7)
The vectors of the normal gravity γ and the gravity g are different in their magnitude and their direction. The
difference in the magnitude is called the gravity anomaly defined by:
∆g = gP − γQ
(1.8)
where gP is the (reduced) gravity at the point P on geoid and γQ denotes the normal gravity at point Q on the
reference ellipsoid. See e.g. Hofmann and Moritz (2005) or Vanicek and Krakiwsky (1982). The directional
difference between the gravity and the normal gravity is called the deflection of the vertical and has two
components: the north-south component ξ, and the east-west component η defined by
(
ξ =Φ−φ
η = (Λ − λ) cos φ
(1.9)
in which (Φ, Λ) are the astronomical latitude and longitude or astronomical coordinates and (φ, λ) are the
geodetic latitude and longitude on the ellipsoid coordinates. See, e.g. Vanicek and Krakiwsky (1982) and
Torge and Müller (2012) for the definition of astronomical and geodetic coordinates.
The distance between the points P and Q is the geoid height N . The geoid height or the geoid undulation can
be obtained from the disturbing potential T and the normal gravity γ using:
N=
T
γ
(1.10)
The second derivative of the gravitational potential, called the gravity gradients, are defined as follows:
∇2 V = ∇g.
(1.11)
The gravity gradients consist of 9 components Vij where i = 1, 2, 3 and j = 1, 2, 3 define the axes of the
coordinate system in which the derivatives are taken. For more details on the definition of different functional
of the gravitational potential as well as their interrelations see, e.g., Hofmann and Moritz (2005) or Torge and
Müller (2012).
There are currently various observation techniques and instruments to measure the functionals of the gravitational
potential. For example the absolute and relative values of gravity can be measured by absolute and relative
gravimeters (Xu, 2010). The deflection of vertical can be obtained by the observations from zenith cameras and
GPS coordinates (Hirt et al., 2010). The geoid heights are derived based on the combination of GPS-levelling
and gravimetric data (Torge and Müller, 2012). In addition, it is also possible to determine geoid heights over
the oceans based on satellite altimetry data (Bosch, 2002, Lee-Lueng and Cazenave, 2000). Finally, gravity
gradients are observed on ground using the torsion balances or from space using satellite gravity gradiometery.
These observations are different in the sense that they contain different spectral content depending on the
resolution and accuracy of the corresponding instrument. These functionals can be used to determine the
gravitational potential as the mother function.
The direct measurement of the geopotential difference is theoretically possible based on the relativistic approach
(Bjerhammer, 1975) using high precision clocks. The approach -where the gravitational redshift from clock
reading at different places is observed- offers a new technique for the direct measurement of the potential
differences in continental distances without satellite systems (Bjerhammer, 1985). The quality of this method
is highly dependent on the precision of clocks. The research in this field is still ongoing to make use of modern
measurement techniques for the determination of time and frequency using atomic clocks.
7
According to equation (1.2), an accurate determination of the Earth’s gravity field would be possible if sufficient
information about the Earth’s structure and mass densities were available. But due to the lack of such information,
there is no exact analytical way to determine the gravity. The only way to obtain information about it,
is to measure it. Gravity can be measured on the Earth’s surface (terrestrial gravimetry), by an aircraft
(airborne gravimetry) or from space using observations provided by the satellite missions (satellite gravimetry).
Terrestrial gravimetry consists of point-wise observations using relative or absolute gravimeters which are of
high accuracy and precision. The coverage of such data is often very poor, inhomogeneous and limited to
some areas. In addition terrestrial gravimetry is very time consuming and expensive. Airborne gravimetry
is an efficient way to provide accurate high-resolution gravity data on regional scales. With current airborne
gravimetry systems the gravity can be obtained at a spatial resolution of 2 km with an accuracy of 1 − 2 mgal
(Alberts, 2009).
Observing the Earth’s gravity field from space has been possible since the early 1960’s. A noteworthy feature
of satellite techniques is the availability of homogeneous observations on the global scale which has not been
possible before. In the last four decades, several low-Earth orbiting satellites have been launched and valuable
satellite-based data are provided. Table 2.1 gives an overview of some selected past as well as the current
satellite mission. Based on the data provide by these missions, many gravity models have been released in
terms of spherical harmonic expansions of the Earth’s gravitational potential. The quality of these models has
been rapidly improved as the latest advanced sensors were employed in the missions.
Mission
name
Year
launched
Altitude
(km)
Inclination
(degrees)
Tracking
method
Observation
technique
GEOS-3
1975
820
115
SLR
Altimetry
GeoSAT
1985
800
108
SLR
Altimetry
Topex Poseidon
1992
1330
66
GPS/SLR
Altimetry
CHAMP
2000
450
87
GPS
SST-hl
GRACE
2002
500
89.5
GPS
SST-hl/ll
GOCE
2009
250
96
GPS
SST-hl and SGG
2017 (planned)
500
89.5
GPS
SST-hl/ll
GRACE Follow on
Table 2.1: Some of past and current dedicated satellite missions used for gravity field determination.
A new era of satellite gravimetry began in the year 2000 when the CHAllenging Minisatellite Payload (CHAMP)
was placed into orbit. CHAMP mission was followed by the Gravity recovery and climate experiment (GRACE)
in 2002 and Gravity field and steady-state Ocean Circulation Explorer (GOCE) in 2009. The GRACE twin
satellites, for the first time, provide valuable information about the time variable components of the Earth’s
gravity field in long and medium wavelength. The innovative observation technique in the GRACE mission
is the K-band ranging system which measures the range between two satellites with a micrometer accuracy
(Tapley et al., 2004). GOCE carries the first-ever gravity gradiometer in space and is about to supply an
unprecedented level of accuracy in determining the gravity of the Earth. Follow-on gravity missions are
now being designed and prepared to operate in a very near future with the idea of sensor integration and
data combination (Hofmann and Moritz, 2005). Rummel et al. (2002) gives more details on the principle of
8
dedicated satellite missions and their aims.
There are mainly three observation techniques for the recovery of the Earth’s gravity field from space: satellite
altimetry, satellite-to-satellite tracking (SST) and satellite gravity gradiometry (SGG). With the satellite altimetry
it is possible to measure the distance from the satellite to a reflecting surface using the radar (and laser)
techniques to determine the sea level. The outcome of the satellite altimetry is the mean sea level which
results in a good approximation of geoid heights in the oceans and seas. In addition, the sea level slope is a
good approximation of the deflections of the vertical and sea surface curvature can be translated to the vertical
gravity gradients. See Bosch (2002) for more details about satellite altimetry and its application in geodetic
science.
Generally speaking, there are two important steps which should be specified in gravity field modelling from
satellite data:
• An approach to set the link between satellite observables and the Earth’s gravitational potential
• A method to represent the gravitational potential on the Earth’s surface or above
Figure 2.1: Recovery of the Earth’s gravity field based on different satellite techniques. The observations from
satellites are, first, mathematically linked to a functional of the Earth’s gravitational potential. In
the next step, the gravitational potential is determined in an inversion process using appropriate set
of base functions.
Figure 2.1 displays different steps for the recovery of the gravity field from satellite data. In the first step,
the observations from satellite missions should be linked to a functional of the Earth’s gravity field. Then the
gravity field shall be represented on the Earth’s surface using a set of appropriate base functions. For this step,
the Earth’s gravity field parameters should be solved for by inverting a large system of equations which is often
ill-posed.
2.1 Precise orbit determination
9
In this chapter, several approaches for the functional link between satellite data and the gravity field will be
considered. More details on the SST and SGG techniques are given which will be used, further, for global and
regional gravity field modelling. The issue of inversion for the gravity field representation, which is the main
focus of this PhD thesis, will be investigated in the next chapters.
2.1 Precise orbit determination
The position and velocity of the satellites play the central role in all techniques for the recovery of the Earth’s
gravity field from satellite data. One reason is that the orbit of the satellites, i.e. the positions and velocities, are
affected by the Earth’s gravitational field. Therefore, the precise determination of the satellite orbits is essential
for gravity field modelling. In addition, the precise orbit data are necessary to locate in-orbit observations
such as range and range rates from GRACE or SGG data from GOCE. Hence, one important step for gravity
field modelling is to precisely determine the orbit of the satellite(s). There are several methods for precise
orbit determination. Kinematic orbit determination, dynamic orbit determination and reduced dynamic orbit
determination can be mentioned for instance. For more details concerning the precise orbit determination see
for example Kang et al. (2006), Jäggi et al. (2007), Montenbruck and Gill (2000), Kroes (2006), Bisnath (2004)
and Zaho (2004).
In gravity field determination based on satellite data, the position of Low Earth Orbiter (LEO) satellites can be
assumed to be known. Therefore the precise orbits are determined beforehand and then gravity field parameters
are estimated. This method is known as two-step approach. However, it is possible to improve the satellite
orbit along with the gravity field parameters simultaneously. In this one-step approach the SST-hl (high-low)
data from the GPS satellites as well as the SST-ll (low-low) data are employed to determine the orbit of the
LEO satellite in addition to the Earth’s gravity field parameters. In the one-step approach, the orbit of the GPS
satellites are assumed to be precisely known and thus fixed. One can even try to improve the GPS orbit at the
same time with the LEO orbit and the gravity field parameters. This integrated approached is proposed by Zhu
et al. (2004). The idea was to use all available data from GPS, GRACE and CHAMP satellites as well as the
ground-based GPS code and phase data for the simultaneous determination of GPS and LEO orbit as well as the
gravity field parameters. They concluded that this approach improves the accuracy of the ephemerides for the
GPS, GRACE and CHAMP satellites in addition to the geocenter variations and the gravity field parameters,
compared to stepwise methods. The benefit of this approach is that the equation system to be solved for, gains
stability from high satellites and sensitivity from low satellites.
In the context of this thesis, the positions and velocities of the LEO satellites are assumed to be fixed during
gravity field modelling. No orbit determination is included here and only the Earth’s gravity field parameters
are to be estimated in a two-step approach.
2.2 Gravity field from SST data
Satellite-to-satellite tracking data or SST are among the most important satellite-based data sets which are
sensitive to the medium and short wavelengths of the Earth’s gravity field. According to Rummel et al. (1978),
the advantageous characteristics of SST are:
• continuous tracking between satellites,
• possibility to maintain an ideal observation geometry and
• sensitivity to the medium and short wavelengths of the gravity field.
One can distinguish between SST-hl mode and SST-ll. The former technique, which was first proposed by Kaula
(1966), includes position and velocities of one or more low Earth orbiting satellites which are continuously
provided by satellites at high orbits (GPS satellites for instance). The CHAMP is using SST-hl for example.
However this technique is not that different from conventional tracking of satellites from ground stations
(Rummel et al. 1978) and hence it is not capable of recovering medium wavelengths of the gravity field.
Wolff (1969) proposed the idea of low-low SST using a satellite pair, which is more sensitive to the medium
10
and short wavelengths of the gravity field. His idea became reality about thirty years later in March 2002 when
the GRACE twin satellites were placed into the orbit. SST-ll consists of inter-satellite ranging products which
are known as range, range rates and range accelerations. Gravity field recovery from GRACE observations
combines both the SST-hl and SST-ll techniques to achieve a spatial resolution down to 400 km on the Earth’s
surface based on a month of data. Figure 2.2 displays the concept of SST in both high-low and low-low
constellation.
Figure 2.2: Concept of SST high-low and SST low-low applied in the GRACE mission.
An important step in gravity field modelling based on SST data is to set a link between these data and the
gravitational potential. Two physical laws are usually used in satellite geodesy for this purpose:
• Newton’s law of motion: Combining the Newton’s second law of motion, (f = mg) with the Newton’s
universal law of gravitation yields
r̈ = ∇V.
(2.1)
Therein r̈ denotes the acceleration vector of the satellite and V is the gravitational potential of the Earth.
Based on this law, there are roughly three approaches that are in use at present for the Earth’s gravity
field recovery: the variational approach, the short arc approach and the acceleration approach.
• Energy conservation law: In mechanics, conservation of energy is
C =E+V
(2.2)
where E and V are the kinetic and potential energy, respectively. C denotes the total energy which is
conserved over time. This law can be used in gravity field modelling as the energy balance approach.
In the following, these approaches are explained briefly with emphasis put on the energy balance approach
which will be used further in our global and regional gravity field modelling.
11
2.2.1 Variational approach
The variational approach is the traditional method to determine gravity field parameters. It can be either a
one-step approach or a two-step approach. According to Reigber (1989), the equation of motion has the form
r̈ = f (r, ṙ, p)
(2.3)
which describes the acceleration of a satellite as a function of initial positions r, velocities ṙ and a set of
parameters p to which the accelerations are sensitive. The set p includes two types of parameters:
• Internal or arc-dependent parameters
– state vector at each epoch,
– drag and solar radiation pressure parameters.
• External or arc-independent parameters
– gravity field parameters,
– tidal parameters,
– Earth rotation parameters.
The parameters p have to be estimated in an iterative process due to the non-linearity of the observation equation
(2.3) with respect to the vector p . The linearisation process is done through computing the partial derivatives of
the acceleration vector r̈ with respect to the unknown vector p. See also Beutler et al. (2010) for more detailed
description of the variational approach.
2.2.2 Short arc approach
The short arc approach is a variant of the variational approach explained in the previous section. The idea of
using short arcs for gravity field recovery is to control accumulated effects of disturbing forces. Moreover, a
kinematic orbit determination cannot provide continuous orbit data over a long period of time (i.e. more than a
year). The reasons for that are gross errors and gaps in SST observations as well as orbit manoeuvres or other
events (Mayer-Gürr et al., 2005). Hence, it is logical to restrict the analysis to several short arcs. The short-arc
approach is based on Newton’s equation of motion which is formulated as a boundary value problem in the
form of a Fredholm integral equation. For every short arc in the time period, the solution of equation (2.1) with
boundary values rA = r(tA ) and rB = r(tB ) reads (Schneider, 1968);
r(τ ) = (1 − τ )rA + τ rB − t2AB
Z1
K(τ, τ 0 )r̈(τ 0 )dτ 0
(2.4)
τ 0 =0
where τ is a normalized time variable at which the position vector is desired. τ is defined as
τ=
t − tA
, tA ≤ t ≤ tB ,
tAB
and τ 0 is the integration variable for the given forces r̈. The kernel K(τ, τ 0 ) is
(
τ (1 − τ 0 ), τ ≤ τ 0
K(τ, τ 0 ) =
.
τ 0 (1 − τ ), τ 0 ≤ τ
(2.5)
(2.6)
In equation (2.4), the position vector r is used directly as the observation and no numerical differentiation is
needed. The short-arc or the integral equation approach has been successfully used in a series of gravity field
modelling from CHAMP kinematic orbit (Mayer-Gürr et al., 2005), and GRACE K-Band Ranging (KBR) data
(Mayer-Gürr, 2006).
12
2.2.3 Acceleration approach
The acceleration approach is a direct application of equation (2.1). The accelerations of the satellite at discrete
points i are used as the observed values to determine gravity field parameters (Reubelt et al., 2003). At each
discrete point i, three observation equations can be written to set up the linear system of equations:

∂V
 ∂x 


 ∂V 

 .
=

 ∂y 
 ∂V 
∂z i

 
Vx

∇Vi = Vy 
Vz i
(2.7)
Since the output of the precise orbit determination is the position vector, the acceleration vector r̈ should
be derived by two times numerical differentiation of the position vector r. The drawback of this approach
is that numerical differentiation of noisy data results in noise amplification especially at higher frequencies.
To overcome this problem some kind of regularization is necessary for high-resolution gravity field recovery.
Besides, numerical differentiation includes fitting a polynomial of a certain degree defined at a set of epochs.
Thus the derivative of this polynomial can be obtained analytically and consequently the velocity and acceleration
vectors can be evaluated (Lio, 2008). In order to obtain a rather good approximation of accelerations at points
i, high degree polynomials should be used. Reubelt et al. (2006) showed that the degree of this polynomial
should be at least 8. This leads, however, to instabilities in the numerical differentiation process and tailored
algorithms must be used. Lio (2008) used an average acceleration scheme for processing real CHAMP and
GRACE kinematic orbits and concluded that satellite acceleration derived from kinematic orbits can be used
for high quality Earth’s gravity field modelling. The acceleration approach, in the case of GRACE KBR data has
a slightly different formulation. It is sometimes called the difference acceleration approach since it deals with
relative quantities. According to Rummel (1979), to derive the equation of difference acceleration approach for
GRACE-type observations, one can start from the position vector between two satellites rAB
rAB = rB − rA ,
(2.8)
where rAB is the difference of position vector of the satellites in an Earth-fixed frame. The inner product of
this vector with itself gives the square of the range ρ:
ρ2 = rAB · rAB .
(2.9)
Taking the first derivative of equation (2.9) yields
ρρ̇ = rAB · ṙAB .
(2.10)
ρ̇ and ṙAB are range-rate and the velocity difference vector, respectively. Equation (2.10) can be rewritten as
ρ̇ =
Therein
rAB
· ṙAB .
ρ
(2.11)
rAB
is the orthonormal line of sight vector or briefly, hereafter, LOS vector:
ρ
eLOS =
rAB
.
ρ
Substituting (2.12) into (2.11) and taking its time derivative results in the range-acceleration ρ̈:
(2.12)
13
ρ̈ = ėLOS · ṙAB + eLOS · r̈AB
(2.13)
where r̈AB is the acceleration difference between the two satellites. Rearranging (2.13) and replacing r̈AB by
∇VAB gives the final equation of the (difference) acceleration approach:
eLOS · ∇VAB = ρ̈ +
ρ̇2 |ṙAB |2
−
ρ
ρ
(2.14)
where |.| denotes the lengths of a vector. Equation (2.14) indicates that the projection of the acceleration
difference of the satellite pair onto the LOS vector can be linked to the inter satellite data products range,
range-rates and range-acceleration.
The left hand side of this equation contains the gravity field parameters to be estimated (depending on the type
of representation) and the observables are on the right hand side. The range rate ρ̇ and the range accelerations
ρ̈, are derived by numerical differentiation of the biased range and the range rate ρ̇ respectively. Therefore
these quantities are affected by the disadvantages of the numerical differentiation (noise amplification by
differentiating). The range ρ and velocity difference ṙAB are numerically derived from GPS data and therefore
their accuracy does not match the accuracy of ρ̇. Thus equation (2.14) without any modification cannot be
suitable for high quality gravity field recovery from GRACE data. Lio (2008) presented two modified variants
of the acceleration approach; 3-point range-rate combination (3RRC) and 3-point range combination (3RC)
approach to reduce the role of GPS-derived quantities in the modelling. The idea of the 3RRC approach is to
compute radial components of velocity differences from KBR data and thus to reduce the impact of GPS data
on the overall error budget. In the 3RC approach the velocity term is totally removed from the observation
equation. Hashemi et al. (2012) used the 3RC approach to determine the static part of the Earth’s gravitational
potential based on the combination of GRACE and GOCE data.
2.2.4 Energy balance approach
As stated before, the energy balance approach is based on the physical law of energy conservation. Based on
equation (2.2) one can assume that the potential energy of a satellite (with negative sign1 ) is equal to the sum
of kinetic energy and a constant (total energy of the closed system) in an ideal case, where no other forces act
on the satellite:
V = E + C.
(2.15)
1
E = kṙk2
2
(2.16)
The kinetic energy of a satellite is given by:
which is the energy per unit mass. Equation (2.15) cannot describe the motion of a satellite in its orbit. The
first reason is the Earth rotation which causes the potential field to be rotational for the satellite. This means the
rotation of the potential field should also be considered in (2.15). Moreover, there are other forces (rather than
the gravitational force) which are considered as dissipating energy in the system. According to Jekeli (1999),
the exact relationship of the energy conservation law in an inertial frame for a satellite is given by
1
V = kṙk2 +
2
Zt
0
1
X
∂V
dt −
∂t
k
Zt
Fk .ṙk dt + C.
(2.17)
0
The term potential has different definition in physics and geodesy. In physics, potential is a feature of particle and is the work
necessary to bring a particle from its initial state to its current position. In geodesy, potential is a feature of the field and is
proportional to the work necessary to bring a particle from infinity to its current position. Therefore potential in geodesy appears
with negative sign compared to physics literature.
14
Therein the second term on the right hand side is the time variation of the potential due to Earth rotation in the
inertial frame which is integrated along the orbit within the time period [0 t]. The third term is the dissipating
energy which is the sum of the known k non-gravitational forces. The potential rotation term can also be written
as (Jekeli, 1999)
Zt
∂V
dt = −ωe (xẏ − y ẋ)
∂t
(2.18)
0
with ωe being the Earth’s angular velocity. x and y are the Cartesian coordinates and ẋ and ẏ are their first
derivatives i.e the velocities. Therefore equation (2.17) can be rewritten as
X
1
V = kṙk2 − ωe (xẏ − y ẋ) −
2
Zt
k
Fk ṙk dt + C.
(2.19)
0
This relation is valid in an inertial reference frame with a rotating Earth. The representation of the gravitational
field is desired in an Earth fixed frame with rotating coordinate system. In Earth fixed frame the ’rotation
potential’ should be considered instead of ’potential rotation’. These names are proposed by Jekeli (1999)
to distinguish between potential in inertial and Earth fixed frames. For the rotation potential in an Earth fixed
frame one can write
1
Zrot = (ωe × r)2
2
(2.20)
1
Zrot = ωe2 (x2 + y 2 ).
2
(2.21)
or
(2.19) in an Earth fixed frame reads:
X
1
1
V = kṙk2 − ωe2 (x2 + y 2 ) −
2
2
k
Zt
Fk ṙk dt + C.
(2.22)
0
It should be noted that all components in (2.19) and (2.22) must be used with respect to inertial frame and Earth
fixed frame, respectively.
These equations are applicable for one satellite such as CHAMP or GOCE. For GRACE observations with the
KBR link, the equation can also be written for two satellites, i.e. potential differences between satellites A and
B. Writing equation (2.19) for the potential differences yields
1
1
VAB = kṙB k2 − kṙA k2 − ωe (xB ẏB − yB ẋB − xA ẏA + yA ẋA )
2
2
t
XZ
−
(FBk ṙBk − FAk ṙAk )dt + CAB .
k
(2.23)
0
The difference of kinetic energy between two satellites can be rewritten in terms of KBR products:
1
1
1
EAB = kṙB k2 − kṙA k2 = (ṙA + ṙB )T ṙAB .
2
2
2
(2.24)
2.3 Gravity field from SGG data
15
Taking the first derivative of (2.12)
ṙAB = ρ̇eLOS + ρėLOS
(2.25)
1
EAB = (ṙA + ṙB )T (ρ̇eLOS + ρėLOS ).
2
(2.26)
and applying this to (2.24) results in
Inserting this equation in (2.23) yields:
1
VAB = (ṙA + ṙB )T (ρ̇eLOS + ρėLOS ) − ωe (xB ẏB − yB ẋB + xA ẏA − yA ẋA )
2
t
XZ
−
(FBk ṙBk − FAk ṙAk )dt + CAB ,
k
(2.27)
0
which relates the KBR data to the potential difference between the GRACE satellites along their orbit. The
energy constant CAB can either be computed using a prior model or estimated along with gravity field parameters
as an additional unknown parameter. The term for dissipating energy can be neglected when dealing with
simulated data. Therefore we exclude this term in our analyses. An advantage of the energy balance or
energy integral approach is that it is linear with respect to the Earth’s gravitational parameters (similar to
the acceleration approach). There is no need for an iterative procedure compared to variational approach. It
is numerically more efficient than the variational approach provided that precise kinematic orbit is available.
This approach has been used to determine several gravits field models; TUM-1s and TUM-2s from CHAMP
data (Gerlach et al., 2003). Han et al. (2002, 2005, 2006) used this approach to model gravity field based on
CHAMP and GRACE data.
It should also be mentioned that the energy balance approach is affected by the accuracy of the velocity vector
which is derived numerically from the GPS data. As a result of numerical differentiation, the noise of the
velocity will be amplified proportional to the frequency. Hence, the resulting correlated noise should be handled
properly in the inversion process (e.g. by frequency dependent weighting). See Han et al. (2006) for more
details on this issue.
The goal of gravimetry, as explained before, is to determine the Earth gravitational potential based on the
data provided by gravimeters. Gravimeters measure the first derivative of the gravitational potential, i.e. ∇V .
Similar to gravimetry, the goal of gradiometry is also the accurate determination of the Earth gravitational
potential. The measured data in gradiometry are the second derivatives of the gravitational potential which are
called gravity gradients. The gravity gradients can be observed on the Earth’s surface using the Torsion Balance
which was invented by Roland von Eötvös at the beginning of 20th century. He obtained, with his instrument,
the precision of 10− 9/s2 or 1 E1 .
The idea of measuring gravity gradients using satellites or SGG is more than 50 years old. However, there was
no realization of SGG until the launch of GOCE in 2009. According to the GOCE mission objectives (Gruber
et al., 2010) the goal is to achieve an accuracy of 1 mgal for gravity anomalies or 1 − 2 cm of geoid heights at a
spatial resolution of 100 km based on observed gravity gradients on board the GOCE satellite. For more details
on the concepts and principles of the GOCE (Rummel et al., 2012). In this section, the principle of gravity
field modelling based on GOCE gradiometry is briefly explained to the extent which fulfils the purpose of this
thesis.
1
The CGS unit for gravitational gradient is named Eötvös in his honour.
16
2.3.1 Gravity gradiometry
Equation (2.7) describes the first derivative of the gravitational potential V . Since the observations in gravity
gradiometry are the second order derivatives of the gravitational potential, one needs to apply the gradient
operator to equation (2.7) which yields:
∂2V
 ∂x2

 2
∂ V
=
 ∂y∂x

 ∂2V
∂z∂x

Vjk
∂2V
∂x∂y
∂2V
∂y 2
∂2V
∂z∂y

∂2V
∂x∂z 


∂2V 

∂y∂z 

∂2V 


Vxx Vxy Vxz
= Vyx Vyy Vyz 
Vzx Vzy Vzz
.
(2.28)
∂z 2
The 3 × 3 matrix Vjk is called the gradient tensor (also gravity tensor) which is a symmetric matrix. This
implies that:


Vxy = Vyx
Vxz = Vzx


Vzy = Vyz .
(2.29)
In addition, since the gravitational potential is a harmonic function outside the Earth, it fulfils the Laplace’s
equation
∆V = Vxx + Vyy + Vzz = 0.
(2.30)
According to equations (2.29) and (2.30), only five out of nine components of the gradient tensor are linearly
independent. Equation (2.28) is the basic equation of gravity gradiometry. The components of the gradient
tensor are observables and the gravity field parameters (e.g. spherical harmonic coefficients) are to be estimated
based on these measurements. This makes the the determination of gravity field based on gravity gradients
a straightforward problem provided that the components of the gradient tensor are really measured in the
corresponding Earth fixed frame where the representation of V is desired. In contrast, the direct measurement
of gravity gradients in an Earth-fixed frame is not easily possible, especially on board an Earth orbiting satellite.
Therefore, some coordinate transformations are necessary in order to use (2.28).
2.3.2 From the GOCE observation frame to the Earth fixed frame
Figure 2.3 illustrates the observation frame on board the GOCE satellite. Six accelerometers are placed along
three axes of a local coordinate system which is called Gradiometer Reference Frame or in brief GRF.
17
Figure 2.3: Different coordinate systems used in connection with GOCE data. The GOCE measurements are
obtained in the GRF on board GOCE satellite. The representation of the gravity field is desired in
geocentric Earth-fixed frame or EF. The LNOF is a coordinate system which is used to connect the
observations to the gravity field parameters.
To convert gravity gradients from GRF to the Earth fixed frame, another interim frame is used in GOCE
standards known as the Local North Oriented Frame or LNOF. LNOF is defined as follows:
• The origin is located at the nominal satellite center of mass with spherical coordinate (r, φ, λ).
• The Z axis is defined as the vector from the geocenter to the origin of LNOF pointing outwards.
• Y is parallel to the normal vector to the plane of the geocentric meridian of the satellite center of mass,
pointing westward. The direction of the Y axis makes the LNOF a right-handed frame.
• The X axis points the geodetic north pole and is parallel to the normal vector to the plane defined by Y
and Z.
Figure 2.3 shows LNOF in connection with GRF and the Earth fixed frame (EF). See also (Gruber et al., 2010)
for the definition of different frames used for GOCE data processing. To convert the gravity gradients from
GRF to LNOF the following relation is used:
LN OF
GRF
Vjk
= R̂T Vjk
R̂
(2.31)
GRF and VLN OF are gradient tensors in GRF and LNOF, respectively. The rotation matrix R̂ is a
where Vjk
jk
3 × 3 orthonormal matrix where
R̂T = R̂−1
(2.32)
18
which implies
R̂T R̂ = R̂R̂T = I
(2.33)
GRF
LN OF T
R̂ .
Vjk
= R̂Vjk
(2.34)
and consequently
The rotation matrices R̂ are unique for each observation point along the GOCE orbit. The last step will be to
establish the relation between gradients in the LNOF and the Earth-fixed frame. It can be shown that the gravity
gradients in the LNOF can be written in terms of the gravity gradients in the Earth-fixed frame as (Koop, 1993)


LN OF (r, φ, λ) = 1 V (r, φ, λ) + 1 V (r, φ, λ)

Vxx

r
φφ

r
r2




1

LN OF (r, φ, λ) = V LN OF (r, φ, λ) =

Vxy
(− tan φVλ (r, φ, λ) − Vφλ (r, φ, λ))

yx

2
r cos φ





V LN OF (r, φ, λ) = V LN OF (r, φ, λ) = − 1 Vφ (r, φ, λ) + 1 Vrφ (r, φ, λ)
xz
zx
r2
r

1
1
1

LN OF (r, φ, λ) = V (r, φ, λ) −

Vyy
tan φVφ (r, φ, λ) + 2
Vλλ (r, φ, λ)

r

2

r
r
r cos2 φ



1
1

LN OF (r, φ, λ) = V LN OF (r, φ, λ) =


Vyz
[ Vλ (r, φ, λ) − Vrλ (r, φ, λ)]
zy


r cos φ r



V LN OF (r, φ, λ) = V (r, φ, λ)
rr
zz
(2.35)
in which the first and second derivatives of the potential are expressed in terms of curve-linear spherical
coordinates. The evaluation of Vr , Vφ and Vλ as well as Vrr , Vrφ , Vφφ , Vφλ and Vλλ depends on the type
of base functions used to represent the gravitational potential V . For the evaluation of these derivatives using
spherical harmonics, see, e.g., Ditmar and Klees (2002) or Koop (1993). In Chapter 6, we determine the first
and second derivatives of the gravitational potential using the SRBF.
2.4 Evolution of global gravity field models and state-of-the-art
A rather complete list of the global gravity field solutions is provided by GFZ (2013). Over 130 global solutions
have been determined since 1966 up to the present time. The accuracy and resolution of these models have
been rapidly improving due to the availability of precise and advanced observation techniques. Before the
launch of the CHAMP mission in 2000, the global models (based on satellite data) were limited to the low
frequencies of the Earth’s gravity field. Figure 2.4 illustrates the contribution of the current satellite missions
to the improvement of the gravity field determination in frequency and space domains. Moreover, to see the
impact of current satellite missions on the resolution and quality of the Earth’s gravity field, we compare several
global models which are determined based on the available satellite data of their time. Table 2.2 gives the details
of these models. The error degree amplitude of these global models are shown in figure 2.5 in terms of geoid
heights. In addition, the cumulative geoid errors of these models are shown in figure 2.6.
The oldest model which is considered here is the model GRIM5S1 (Biancale et al., 2000) which was published
in 1999. The model has been determined based on the available tracking data of 21 satellites with different
orbit altitude and inclination. The error amplitudes are rapidly increasing as the harmonic degrees beyond
10 are included. The geoid error is about 15 cm at its highest resolution. A remarkable improvement at low
frequencies (n < 50) was achieved after the launch of the CHAMP mission. The launch of the GRACE in 2002,
brought a step forward in the determination of global gravity field in long and medium wave lengths. Compared
to CHAMP models, GRACE data could improve the quality of gravity field determination, up to two orders of
magnitude. This improvement was achieved based on a month of GRACE data only. The error amplitude was
2.5 Follow-on missions
19
data used
Nmax
year
orbit of 21 satellites
99
1999
EIGEN-CHAMP03S
CHAMP
140
2004
GFZ monthly
GRACE
120
2007
ITG-Grace2010s
GRACE
180
2010
GOCE and GRACE
250
2012
geo-potential model
GRIM5S1
GOCO03S
TIM-R4
GOCE
250
2013
ITG-Goce02
GOCE
240
2013
Table 2.2: Some selected geopotential models determined from 1999 until 2013 based on the state-of-the-art
observation techniques. The second column shows the data used to determine the gravity field model.
See GFZ (2013) for more details about these models.
further reduced as more GRACE data were included in the modelling of the static gravity field. Since March
2009, GOCE observations increased the resolution and quality of the higher degrees of the Earth’s gravity field.
GOCE cannot compete with the accuracy of the medium long wavelengths determined by GRACE. GRACE and
GOCE are now considered as the complementary missions. Thus combining GRACE and GOCE observations
is currently the state-of-the-art for high resolution gravity field modelling based on satellite data only. See also
Pail et al. (2013) for more details on the recent developments and accuracies of the global geo-potential models.
The geodetic satellite missions have provided a large amount of valuable observations for the geoscientific
community. Due to the availability of such data many geophysical phenomena are better understood in the
last decade. Investigations are still ongoing to improve the quality of satellite data to extract more and more
information out of available data. Apart from that, there is no doubt about the necessity of launching new
satellite missions to keep acquiring useful data from space. The GRACE follow-on is to be launched in 2017 to
continue monitoring changes of the Earth’s gravitational potential. It is a rebuild of GRACE with the possibility
to test the inter-satellite laser ranging technique to increase the precision of SST-ll data (Sheard et al., 2012).
Moreover, there are several research studies carried out to design and propose new concepts for future satellite
missions. See Flury and Rummel (2005) and Panet et al. (2012) for more technical discussion and details.
20
Figure 2.4: The contribution of current satellite missions to the improvement of the short, medium and the long
wavelengths of the gravity field. The frequency and spatial resolution shown here are just rough
estimations. The dotted lines indicate the uncertainty for the definition of borders between long,
medium and short wavelengths as well as the exact resolution of the satellite missions.
21
Figure 2.5: Error degree amplitudes in terms of geoid heights. The results are based on several global models
from 1999 until 2013. All models are satellite-only solutions. The solutions are improved with the
new observations from satellite data. As it can be seen from 1999 until 2013 the accuracy of global
models is improved at least two orders of magnitude. In addition the resolution is also increased
from about n = 25 in 1999 up to n = 220 in 2013. For the Kaula rule see Section 3.1.2
.
22
Figure 2.6: The cumulative geoid errors for several global models in the last decade. The current accumulated
geoid error is about 14 cm for GRACE-only models up to degree 120 and 11 cm for GOCE-only
solutions up to degree 250.
23
In the previous chapter, we discussed the general form of different approaches for the connection between
gravitational potential V and a set of SST-hl and/or SST-ll observations. These approaches provide (directly or
indirectly) the information about the gravitational potential or its derivatives at satellite altitude. For example
the energy balance approach supplies the gravitational potential (or potential differences between satellites in
the case of GRACE) along the orbit. The difference acceleration approach gives acceleration differences along
the orbit which are projected onto line of sight vector. After setting the functional link between the data and
the potential field, the goal of gravity field modelling is to construct the potential field on the Earth’s surface or
above it using an analytical continuous function which represents the feature of the gravitational potential.
The mathematical description of this problem can be expressed as follows:
Let Ω be a sphere with radius R and (φ, λ) the geographical latitude and longitude respectively. We define r to
be the position vector of a point on or above Ω, as:
r = r[cos φ cos λ cos φ sin λ sin φ]T , |r| = r ≥ R.
(3.1)
The potential values (or its functional) vi , are given at discrete observation points ri , the goal is to find a
function f such that:
f (ri ) = vi + ei , i = 1, 2, ..., I
(3.2)
where ei denotes the errors in the observations. Since the gravitational potential is a harmonic function (Moritz
1980), f must also be a harmonic function to represent the characteristics of the field. In an ideal case,
the function f should represent the error-free values vi and reveal the features of the potential field with no
uncertainty. In reality f shall be approximated using a set of known functions, called the base functions, and
their corresponding coefficients.
Polynomials are among the most important and interesting approximating functions in numerical analysis and
modelling. Polynomial approximation is an old subject in mathematics and there are numerous theorems
describing the properties of these functions. Perhaps the most important theorem for polynomial approximation
is the theorem of Weierstrass (Moritz and Sünkel 1978). It states that every continuous function f can be
uniformly approximated by a polynomial with arbitrary accuracy. This polynomial approximation can be
written as
f (ri ) =
K
X
αk Bk (ri )
(3.3)
k=0
which means the function f is approximated by a linear combination of K base functions Bk and corresponding
coefficients αk . Putting equations (3.2) and (3.3) together, one can write the generic form of gravity field
modelling based on observed values vi :
K
X
αk Bk (ri ) = vi + ei , i = 1, 2, ..., I.
(3.4)
k=0
Based on this equation, gravity field modelling is, in practice, the determination of unknown coefficients αk ,
associated with the known base functions Bk . There are some other alternative terms for gravity field modelling,
in the literature: Gravity field analysis, gravity field determination, gravity field inversion or sometimes,
gravity field parametrization can be mentioned for instance.
24
The interpretation of the coefficients αk and the information they contain, is directly dependent on the choice
of the base functions Bk . For example, if the base functions are defined as harmonic functions, the scaling
coefficients αk are their corresponding amplitude and reveal the spectral properties. Therefore the proper
choice of the base function, is an important step for gravity field modelling. In the following, we describe the
spherical harmonics (SH), which are the most commonly used functions for the approximation on the sphere
and in particular for gravity field modelling. Later in this chapter, we discuss the advantages and disadvantages
of SH and introduce other alternatives. Among other alternatives we put emphasis on the SRBF which will be
considered in the next chapter.
3.1 Spherical harmonics (SH)
The well-known base functions (polynomials) used for gravity field modelling, are the spherical harmonics.
These functions are a great tool for global applications due to their global support. They are characterized
by the nice feature of orthogonality and the numerical implementation of them is straightforward. Spherical
harmonics have different applications in various disciplines and therefore are seen from different perspectives.
In approximation theory, spherical harmonics are the basis for harmonic homogeneous polynomials of a certain
degree on the sphere (Freeden et al., 1998, Müller, 1966). Spherical harmonics are also used in physics and
quantum mechanics as the eigenfunctions of angular momentum operators (Edmonds, 1957). In potential
theory, spherical harmonics can be seen as the solution of the Laplace equation (Heiskanen and Moritz, 1967)
and are also considered as the eigenfunctions of the Laplace operator. Moreover, they can be interpreted as the
generalization of the Fourier transform to the spherical coordinates and therefore share important properties
with ordinary Fourier series in one or more dimensions (Colombo, 1981).
3.1.1 Mathematical description of SH
A square integrable function f , defined on the sphere Ω, can be approximated using a series of trigonometric
functions P̄nm (sin φ) cos mλ and P̄nm (sin φ) sin mλ:
f (φ, λ) =
∞ X
n
X
(ānm cos mλ + b̄nm sin mλ)P̄nm (sin φ)
(3.5)
n=0 m=0
with φ and λ being the surface spherical coordinates on the unit sphere. ānm and b̄nm are the normalized
spherical harmonic coefficients of degree n and order m. These coefficients are also called the Stokes coefficients
in the literature. The fully normalized associated Legendre functions P̄nm are a solution of Legendre’s differential
equation (Heiskanen and Moritz, 1967). These functions have also explicit relation to the mth derivative of the
Legendre polynomials Pn of degree n
Pnm (sin φ) = (cos φ)m
dm
Pn (sin φ)
(d sin φ)m
(3.6)
where Pnm (sin φ) are the non-normalized Legendre functions.
The functions P̄nm (sin φ) cos mλ and P̄nm (sin φ) sin mλ are the spherical harmonic base functions, employed
to approximate the function f . In the literature and text books, spherical harmonics are usually denoted by
c (φ, λ) and Ȳ s (φ, λ) as:
Ȳnm
nm
(
c (φ, λ) = P̄
Ȳnm
nm (sin φ) cos mλ
.
(3.7)
s
Ȳnm (φ, λ) = P̄nm (sin φ) sin mλ
Figure 3.1 illustrates the normalized spherical harmonics of degree 4. The approximation procedure of the
c and Ȳ s are similar to the unknown
function f is in fact to measure, how much the known functions Ȳnm
nm
function f . The tool for this ’similarity measurement’ is the inner product, or the metric of the space. The inner
25
Figure 3.1: Normalized spherical harmonics of degree 4
product is defined as a result of the square integrability condition. Square integrability implies that the integral
of f 2 should be bounded. In mathematical form, the function f is said to be square integrable if
ZZ
f (φ, λ)2 dΩ < ∞.
(3.8)
Ω
Therein, dΩ = sin φdφdλ is the surface element on the sphere. Thus f belongs to the space of all square
integrable functions denoted by L2 (Ω). Using the square integrability condition (3.8), the inner product of the
functions f and g is defined as:
ZZ
< f, g >=
f (φ, λ)g(φ, λ)dΩ
(3.9)
Ω
which is bounded by definition. The norm1 of f is also measured by the inner product:
vZ Z
u
p
u
kf k = < f, f > = t
f (φ, λ)2 dΩ.
(3.10)
Ω
The interesting feature of spherical harmonics is their orthogonality relations which can be described by
RR
c (φ, λ)Ȳ c (φ, λ)dΩ = 0 if n 6= p or m 6= q or both
Ȳnm

pq



Ω
RR
s (φ, λ)Ȳ s (φ, λ)dΩ = 0 if n 6= p or m 6= q or both
Ȳnm
pq

Ω

RR

c (φ, λ)Ȳ s (φ, λ)dΩ = 0 always

 Ȳnm
pq
Ω
1
The term ’norm’ used in this thesis, refers to the L2 norm.
(3.11)
26
which means every spherical harmonic function is orthogonal to other spherical harmonics. Finally, the inner
c (φ, λ) or Ȳ s (φ, λ) yields:
product of two similar Ȳnm
nm
ZZ
c
c
Ȳnm
(φ, λ)Ȳnm
(φ, λ)dΩ =
ZZ
s
s
Ȳnm
(φ, λ)Ȳnm
(φ, λ)dΩ = 1.
(3.12)
Ω
Ω
According to the orthogonality relations, if the function f is expanded into a series of spherical harmonics, as
in equation (3.5), the coefficients ānm and b̄nm can be independently computed using the inner product:

RR
c
c (φ, λ)dΩ

f (φ, λ)Ȳnm
ānm =< f, Ȳnm (φ, λ) >=
Ω
RR
s
s (φ, λ)dΩ

f (φ, λ)Ȳnm
b̄nm =< f, Ȳnm (φ, λ) >=
(3.13)
Ω
which expresses that the coefficient ānm and b̄nm are the averages of the inner products of the function f
c (φ, λ) and Ȳ s (φ, λ). Equations (3.5) and (3.13) are also
and the corresponding approximating functions Ȳnm
nm
called spherical harmonic synthesis and spherical harmonic analysis, respectively. In analogy to the Fourier
transform, the power spectrum of the function f is defined by the set of all degree variances σn2 :
n
X
σn2 =
(ā2nm + b̄2nm ).
(3.14)
m=0
Another important property of spherical harmonics is the Parseval’s relation (Colombo, 1981, Kreyszig, 1978):
2
ZZ
kf k =
2
f (φ, λ) dΩ =
∞
X
σn2
(3.15)
n=0
Ω
that states the norm of the function f and the norm of its spherical harmonic expansion are the same. Parseval’s
c (φ, λ) and Ȳ s (φ, λ) constitutes a
relation also indicates that the set of spherical harmonic functions Ȳnm
nm
complete orthogonal set on the sphere. It should also be mentioned that the set of all square integrable
functions on the sphere in addition to the metric defined by inner product, construct a Hilbert space. Among
all square integrable functions in this space, spherical harmonics are unique and carry nice properties such as
orthogonality and totality (Kreyszig, 1978).
Another property of spherical harmonics is the addition theorem, which is a result of the orthogonality of these
base functions. The addition theorem reads:
(2n + 1)Pn (cos ψ) =
n
X
Ȳnm (φi , λi )Ȳnm (φk , λk )
(3.16)
m=−n
where cos ψ is the spherical distance between two points i and k on the sphere and is given by:
cos ψ = sin φi sin φk + cos φi cos φk cos(λi − λk ).
(3.17)
This relation will be further used for the definition of SRBF in the next chapters.
The orthogonality of spherical harmonics, in addition to the fact that they form a complete set of functions
on the sphere are the main reasons that they are widely used for approximation and modelling on the sphere.
Moreover, the solid spherical harmonics:


c (φ, λ)
 1 Ȳnm
rn+1
1

s (φ, λ)

Ȳnm
n+1
r
(3.18)
27
and
(
c (φ, λ)
rn Ȳnm
s (φ, λ)
rn Ȳnm
(3.19)
also satisfy Laplace equation (Hofmann and Moritz, 2005) and have all properties of the surface spherical
harmonics. The exterior solid spherical harmonics (3.19) are valid outside the unit sphere while the interior ones
hold inside the unit sphere. Hence, the exterior solid spherical harmonics are appropriate functions to analyse
the geopotential data observed above the surface of the sphere (i.e. satellite-based observations). Both types
of surface spherical harmonics and solid spherical harmonics are usually referred to as spherical harmonics.
In the following, we also use the generic term spherical harmonics for simplicity but keeping in mind that the
exterior solid spherical harmonics are meant. More complete mathematical descriptions and characteristics of
spherical harmonics can be found in numerous text books and papers, e.g. Colombo (1981), Heiskanen and
Moritz (1967), Moritz (1980), Vanicek and Krakiwsky (1982).
3.1.2 Expansion of the gravitational potential into SH
The equations in Section 3.1.1 are valid for all square integrable functions on the unit sphere with radius R = 1.
These relations can be generalized for spheres with arbitrary radii. For the expansion of the gravitational
potential outside the Earth, it is common to use the exterior solid spherical harmonics (3.18) defined on the
sphere with radius R. The radius R is usually equal to the radius of a sphere which circumscribes the Earth
and its topography (Hofmann and Moritz, 2005) and is known as the Brillouin sphere (Vanicek and Krakiwsky,
1982).
The gravitational potential V outside the Brillouin sphere can be expanded into a series of (exterior) solid
spherical harmonics:
V (r, φ, λ) =
∞
n
GM X R n+1 X
( )
(c̄nm cos mλ + s̄nm sin mλ)P̄nm (sin φ)
R
r
n=0
(3.20)
m=0
wherein r > R is the distance between evaluation point and the center of the Earth, c̄nm and s̄nm are the
corresponding Stokes coefficients. c̄nm and s̄nm are the scaled version of ānm and b̄nm in equations (3.5) and
(3.13) such that

R−n

c̄nm =
ānm


GM
.
(3.21)

−n


s̄ = R b̄
nm
nm
GM
These coefficients can be determined using (solid) spherical harmonic analysis relations:

RR
R

c (φ, λ)dΩ

V (r, φ, λ)( )n+1 Ȳnm
c̄nm =
r
dΩ
.
RR
R n+1 s


s̄
=
V
(r,
φ,
λ)(
)
Ȳ
(φ,
λ)dΩ
 nm
nm
r
dΩ
(3.22)
Similar to (3.14), the degree variances for the gravitational potential can be derived from spherical harmonic
coefficients:
σn2 =
n
X
(c̄2nm + s̄2nm )
m=0
and accordingly the degree standard deviations:
(3.23)
28
v
u n
uX
(c̄2nm + s̄2nm )
σn = t
(3.24)
m=0
which show the energy content of each specific spherical harmonic degree. A rough rule to obtain the degree
variances σn2 without using the coefficients c̄nm and s̄nm is obtained from the autocovariance analysis of
gravimetry (Kaula, 1966):
σn2 ≈
160 × 10−12
.
n3
(3.25)
Using (3.23) and (3.24) one can write
s
σn (c̄nm , s̄nm ) =
160 × 10−12
(2n + 1)n3
(3.26)
which is known as Kaula’s rule of thumb. Kaula’s rule of thumb is considered as the a priori information about
the coefficients c̄nm and s̄nm and is widely used for the regularization of global gravity field modelling using
spherical harmonics. Equation (3.20) is sometimes written as
∞
n
GM X R n+1 X
( )
C̄nm Ȳnm (φ, λ)
V (r, φ, λ) =
R
r
m=−n
(3.27)
n=0
c for m ≥ 0 and also C̄
s
in which C̄nm = c̄nm and Ȳnm = Ȳnm
nm = s̄nm and Ȳnm = Ȳnm for m < 0. The
coefficients C̄nm can be determined by:
ZZ
C̄nm =
R
( )n+1 V (r, φ, λ)Ȳnm (φ, λ)dΩ.
r
(3.28)
dΩ
This alternative representation will be further used in section 3.2 for the relation between spherical harmonics
and kernel functions.
Concerning spherical harmonic analysis using equations (3.22) some remarks should be made:
• Equations (3.22) and (3.13) are important because they show the orthogonality of spherical harmonics.
Nevertheless, the evaluation of Stokes’s coefficients c̄nm and s̄nm is not possible using (3.22) since
the gravitational potential V is not continuously available. Instead, a set of noisy vi at discrete locations
(ri ,φi ,λi ) is measured. Therefore, (3.22) can be rewritten in discrete form for numerical implementations:

PP
1
c (φ , λ )∆Ω

c̄nm =
V (ri , φi , λi ) n+1 Ȳnm
i i

ri
∆φ ∆λ
.
(3.29)
PP
1

s (φ , λ )∆Ω

s̄
=
V
(r
,
φ
,
λ
)
Ȳ
i i i n+1 nm i i
 nm
ri
∆φ ∆λ
The same argument holds for spherical harmonic synthesis using equation (3.20). The gravitational
potential V can be evaluated at discrete points i using given coefficients c̄nm and s̄nm :
V (ri , φi , λi ) =
Nmax
n
X
GM X
R
(c̄nm cos mλi + s̄nm sin mλi )P̄nm (sin φi ).
( )n+1
R
ri
n=0
(3.30)
m=0
The maximum degree Nmax used in the expansion is chosen based on the measured data and the resolution
of the desired model. To be more specific, Nmax is chosen because all coefficients with n > Nmax are
zero or their values are neglected. In this case the function V is said to be band-limited.
29
• The orthogonality of spherical harmonics is always preserved if these functions are continuously available.
In practice these functions are sampled at discrete points i where observations are available. Therefore
the orthogonality relations (3.11) do not hold in discrete form and consequently the Stokes coefficients
cannot be simply determined using (3.22) or (3.29) without a proper quadrature method. If data are
given on a special grid where the circles of latitude are located at zeros of Pn (sin φ), equations (3.29) are
applicable using special quadratures weights (Colombo, 1981). This specific grid is known as the Gauss
grid and the corresponding quadratures method is Gaussian quadratures (Payne, 1971). Although it is
possible to generate or interpolate data on a Gaussian grid, such methods are applicable for data on the
surface of the sphere. For satellite measurements at orbit altitude it is not possible to apply this technique.
Hence the Stokes coefficients cannot be determined using (3.29) and consequently should be calculated
using alternative methods.
3.1.3 Estimation of spherical harmonic coefficients using least-squares adjustment
The coefficients αk (here c̄nm and s̄nm ), can also be estimated using the method of least-squares (Colombo,
1981, Koch, 1999, Vanicek and Krakiwsky, 1982). Least-squares is a method to determine the unknown
coefficients αk with the assumption that the error norm kek is minimum. The least-squares adjustment procedure
for determining the geopotential based on observed values vi on or above the surface can be expressed in matrix
notation. Substituting equation (3.30) in (3.2) yields:
Nmax
n
X
GM X
R
( )n+1
(c̄nm cos mλi + s̄nm sin mλi )P̄nm (sin φi ) = vi + ei
R
ri
n=0
(3.31)
m=0
This equation results in a liner system with I equations (observations) and K = (Nmax + 1)2 unknowns to be
estimated. In matrix notation, (3.31) can be written as
l + e = Ax.
(3.32)
l = [v1 , v2 , ..., vI ]T and e = [e1 , e2 , ..., eI ]T are the observation and error vectors, respectively. The design
matrix AI×K describes the model and is a linear operator which projects the elements of the space of unknowns
onto the observation space. The column vectors of A are the base functions of the approximation problem. For
spherical harmonic analysis, the base functions or the column vectors of A are the spherical harmonics:
A=
∂V (r)
∂c̄nm
∂V (r)
∂s̄nm
(3.33)
with


 ∂V (r) = GM ( R )n+1 cos mλP̄nm (sin φ)


 ∂c̄nm
R r
(3.34)


∂V (r)
GM R n+1



=
( )
sin mλP̄nm (sin φ)
∂s̄nm
R r
and the vector x contains the unknown coefficients c̄nm and s̄nm . The least-squares solution x̂, is obtained
under the minimum error norm condition:
min kAx − lk2Pl
and is given by (Koch, 1999)
(3.35)
30
x̂ = N−1 y
(3.36)
if N−1 exists. The elements of equation (3.36) are

T

N = A Pl A
(3.37)


y = AT Pl l.
Pl is the positive definite weight matrix and is inversely proportional to the covariance matrix of observations
Cl :
Cl ∝ P−1
l .
(3.38)
Introducing the variance factor σ02 , the weight matrix Pl can be related to Cl :
Cl = σ02 P−1
l
(3.39)
which is the stochastic part of the observation equation (3.32). The solution obtained from the least-squares
approach has several nice properties such as unbiasedness, best and unique approximation and minimum error.
The latter is valid only for the normally distributed errors. More details about the method of least-squares
adjustment can be found for example in Koch (1999), Moritz and Sünkel (1978), Vanicek and Krakiwsky
(1982).
To assess the quality of estimated parameters using least-squares method, one can derive the covariance matrix
Cx̂
Cx̂ = σ02 N−1 .
(3.40)
The variance factor σ02 is not known in the beginning of the least-squares adjustment and is usually set equal
to 1. However a measure of this value can be determined after estimating the unknown coefficients using the
following equation (Koch, 1999, Vanicek and Krakiwsky, 1982):
σ̂02 =
êT Pl ê
I −K
(3.41)
where ê = Ax̂ − l is the estimated vector of residuals and I − K is the degree of freedom or the redundancy
of the least-squares adjustment. Using the a posteriori variance factor σ̂02 the estimated covariance matrix of x̂
will be:
Ĉx̂ = σ̂02 N−1 .
(3.42)
The diagonal elements of Ĉx̂ are variances of the estimated spherical harmonic coefficients. Denoting these
variances by σ̂c2nm and σ̂s2nm , the error degree amplitudes are computed as
v
u n
uX
dσn = t
(σ̂c2nm + σ̂s2nm )
(3.43)
m=0
which together with the degree variances (3.23) are used to assess the quality of gravity field models as they
reveal the energy and error contained in each degree. Typical plots of degree variances and error degree
amplitudes are shown in figure 2.5.
31
3.1.4 Disadvantages of spherical harmonics
Spherical harmonic analysis (and synthesis) is straightforward. It is indeed the best analysis tool for globally
(homogeneous) distributed data on the sphere. Optimal spectral localization is possible and interpretation and
assessment of the model in terms of degree and error degree amplitude is rather easy. In contrast to these
advantages, there are also some drawbacks when dealing with spherical harmonics:
• Geopotential models are often used to investigate a particular phenomenon over a certain region (e.g.
ice mass loss in Greenland, water storage in river basins, land uplift in Scandinavia, etc.). In general,
spherical harmonic analysis and the same global Stokes coefficients are used for all these applications.
The global solution using spherical harmonics is equivalent to applying a global filter to the data. This
may lead to over-filtering of the data in some regions. For some applications it is desired to zoom-in
into a specific region and extract as much signal as possible out of the data. For this purpose, spherical
harmonics are not the best choices and regionally adapted base functions should be used.
• Obtaining the solution over a region decreases remarkably the cost of computations compared to global
spherical harmonic solutions. The number of observations and unknown parameters included in the
model setup and consequently the cost of computations will be dramatically reduced. This is especially
demanded for the current and future satellite missions such as GOCE and GRACE follow-on missions
where the expected resolutions of the models are rather high. For example, to obtain a global solution
based on GOCE data up to degree and order n = 250, one needs to deal with an observation equation
with over 63000 parameters to be estimated. A regional model with the same resolution can be achieved
for a region as big as Central Africa with about 6000 unknown parameters where the same or even better
accuracy is expected (see section 6.3.3).
• Due to the globally averaging feature of spherical harmonics, observation errors will propagate globally.
If, especially, errors are limited to a certain region (e.g. ocean tide models, atmospheric effects) all
coefficients and thus the whole global model will be affected (Lemoine et al., 2007).
• Another obvious disadvantage of using spherical harmonics is that these global base functions need
global data distribution as well. As we discussed in (3.3.2), spherical harmonic functions are sampled
at discrete points where data are available. Since these functions are almost non-zero everywhere on the
sphere, data should also be available everywhere on the sphere for proper sampling. As a result of this
all spherical harmonic coefficients depend on all data over the sphere and any change in data (even in a
small region) would require the re-computation of all coefficients.
• If global data are not homogeneously available, one expects to extract more details (the higher frequencies)
out of the data in those regions where a denser distribution is provided. According to the Nyquist-Shannon
sampling theorem (Steven, 1997) the highest frequency, which could be modelled from a given discrete
data set, is twice the sampling interval or one-half of the sampling frequency. If the data sampling rate
is not constant, it is difficult to define the highest frequency (spherical harmonic degree) for the analysis.
This happens always in gravity field modelling since a completely homogeneous data distribution is never
available. It is however possible to include higher spherical harmonic degrees based on the region with
the densest data coverage. Though, this is unnecessary for other regions and one may desire to model the
field using more optimal alternative ways. Choosing low degree spherical harmonics leads to smoothing
the signal in regions with denser data and aliasing problems for the spectrum.
• A very common case in gravity field modelling is to deal with heterogeneous observations such as
combining terrestrial gravity data and satellite-based observations. The heterogeneous data are not
homogeneously distributed and the matter of highest frequency explained above is an issue again. Even
if heterogeneous data are homogeneously available, such data sets contain different frequency content so
that spherical harmonic analysis is not appropriate. Thus dense terrestrial data are better modelled using
localizing base functions.
In principle other base functions can also be used to represent the gravitational potential on the surface of
the sphere. One approach is to use the so called ’mascons’ which refer to mass concentrations. Mascons
32
can be localized in both space and frequency domains and are appropriate for regional gravity field modelling
(Lemoine et al., 2007). Another alternative to spherical harmonics are the SRBF. The SRBF have been recently
used in many research studies to model the gravity field of the Earth on regional scales. The SRBF will be
considered briefly in the following section. In chapter 4, more details about the SRBF will be given for the
regional gravity field modelling.
3.2 Spherical radial base functions (SRBF): A first look
In section 3.1.4, we discussed several disadvantages of spherical harmonics for gravity field modelling. Most of
these drawbacks originate in the fact, that the spherical harmonics are ideal frequency-localizing base functions
and have no measure of space-localization. The reason is, that the recovery of the spectral properties of the field
needs a sort of base functions with global support in the field domain. To overcome the problems mentioned
in 3.1.4, one needs to use base functions which have space-localizing features. In other words, such base
functions should have compact support, that is, the base functions are non-zero in a certain sub-domain and
zero elsewhere. The ideal space-localizing functions are the well-known Dirac functions. The Dirac function
is zero everywhere except at zero and hence has a strict compact support (the support is {0}). Having ideal
space-localizing property, the Dirac function has no frequency-localization instead. A perfect space-localization
cannot be achieved simultaneously with a perfect frequency-localization. This issue is known as the ’uncertainty
principle’ which states, that it is impossible to know exactly where (or when) a certain frequency occurs. See for
example Neumann (1968), Freeden et al. (1998) and Keller (2004). Spherical harmonics (Fourier Transform)
and Dirac functions describe two edges of signal analysis in the frequency and space (time) domain. While
the former needs infinite frequencies to reconstruct a non band-limited signal, the latter needs infinite Dirac
functions to model a continuous signal.
Figure 3.2: Uncertainty principle in space and frequency. Spherical harmonics with ideal frequency localization
and Dirac functions with ideal space localizations are two extreme edges in signal processing.
Kernel functions are a good compromise in between. See also Freeden (1999).
A good compromise between ideal frequency-localization (SH) and ideal space-localization (Dirac) are kernel
functions as illustrated in figure 3.2. The kernel functions are used for pattern analysis or pattern recognition
in many applications. Souza and César (2010) list several kernel functions and basic definitions for different
applications. In the following, we use SRBF as kernel function which provide a balance between frequency and
space localization. These functions are appropriate alternatives to spherical harmonics especially if the gravity
field is to be determined on regional scales.
3.2 Spherical radial base functions (SRBF): A first look
33
3.2.1 Mathematical description of SRBF
To explain the gravity field representation using SRBF, we consider the same setup as in previous section, given
by equations (3.1) through (3.4). For spherical harmonic analysis and synthesis, we used spherical harmonics
Bk and the coefficients αk will be the Stokes coefficients c̄nm and s̄nm accordingly. The same settings hold
for gravity field analysis and synthesis using SRBF; Bk are SRBF and αk will be the corresponding scaling
coefficients.
If we plug equation (3.28) into (3.27)
ZZ
∞
n
X
R n+1 X
V (ri , φi , λi ) =
( )
V (rk , φk , λk )Ȳnm (φk , λk )Ȳnm (φi , λi )dΩ,
ri
m=−n
n=0
(3.44)
Ω
rearranging the order of summation and integration yields
ZZ
V (ri , φi , λi ) =
Ω
n
∞
X
R n+1 X
V (rk , φk , λk )
( )
Ȳnm (φk , λk )Ȳnm (φi , λi ) dΩ.
r
m=−n
n=0 i
|
{z
}
(3.45)
Addition theorem
Using the addition theorem given by equation (3.16), one can write
ZZ
V (ri , φi , λi ) =
V (rk , φk , λk )
Ω
∞
X
R
( )n+1 (2n + 1)Pn (cos ψ) dΩ.
r
n=0 i
{z
}
|
(3.46)
Reproducing kernel function=H(rk ,ri )
Introducing the reproducing kernel function H(rk , ri ), as defined in (3.46), results in
ZZ
V (ri , φi , λi ) =
V (rk , φk , λk )H(rk , ri )dΩ,
(3.47)
Ω
which shows the reproducing property of H(rk , ri ); if rk = ri then the integration of V and H on the right
hand side of (3.47), reproduces V . According to (3.9) the right hand side of (3.47) can be replaced by the inner
product
V (ri , φi , λi ) =< V (rk , φk , λk ), H(rk , ri ) > .
(3.48)
Schmidt et al. (2007) showed that this inner product can be replaced by a series expansion in terms of SRBF
B(ri , rk )
∞
GM X
αk B(ri , rk ).
V (ri , φi , λi ) =< V (rk , φk , λk ), H(rk , ri ) >=
R
(3.49)
k=1
A SRBF at position rk on the surface of the sphere ΩR , is defined as:
B(ri , rk ) =
∞
X
R
( )n+1 (2n + 1)bn Pn (cos ψ)
ri
(3.50)
n=0
where bn are the so-called shape coefficients or the Legendre coefficients and will be discussed later. The
Legendre polynomials Pn (cos ψ) are the function of spherical distance, cos ψ, which is given by equation
(3.17). In the special case where bn = 1 the SRBF will be the reproducing kernel H.
34
Figure 3.3: Normalized SRBF of different resolution. As the maximum degree of expansion increases, the base
functions get narrower. This means the high frequency content can be examined with narrow base
functions while wider base functions are only suitable for the investigation of lower frequencies.
The SRBF should be located at certain positions. See more details in Section 4.2.4.
Equation (3.49) together with (3.50) yields:
V (ri , φi , λi ) =
∞
∞
GM X X R n+1
αk
( )
(2n + 1)bn Pn (cos ψ),
R
ri
k=1
(3.51)
n=0
which is analogous to (3.20). The equivalence of (3.51) and (3.20) indicates that SH and SRBF are two basis
which span the same function space. This is similar to use two different coordinate systems to describe the
elements of a space. Therefore, in an ideal global case, expansion of the gravitational potential V into a set of
spherical harmonics or SRBF lead to the same results from mathematical point of view.
The main feature of SRBF is, that they are dependent on the spherical distance between the data points and the
location of the base functions. The value of a radial base function is maximum at its centre while it oscillates
and decreases in far zones. Figure 3.3 shows six SRBF of different resolution. The resolution is measured
by the maximum degree of expansion in (3.51). As it is obvious from this figure, the higher the resolution is,
the narrower the base function will be. This means, the finer structures of the gravitational potential (higher
frequencies) can be recovered only by narrower base functions.
According to (3.50), SRBF have global oscillations and do not have strict compact support for an ideal space
localization. Nevertheless, the oscillations are rather small in far zones, so that they can be neglected. Therefore
when analysing the gravitational potential using SRBF B(ri , rk ), the corresponding scaling coefficients αk are
predominantly determined by the observations around the centre of B. In chapter 5 we use this feature for the
recovery of the regional gravity field and introduce a new condition for the regularization process.
Equation (3.51) describes the synthesis of the gravitational potential using SRBF (forward modelling) which is
similar to spherical harmonic synthesis given by equation (3.30). The gravity field analysis using SRBF (i.e.
determining scaling coefficients αk ) can be performed by means of spherical convolution integrals. Details
of such numerical integration can be found in Freeden et al. (1998), Freeden (1999) or Schmidt et al. (2007).
Evaluation of scaling coefficients using discrete convolution integrals has the advantage that there is no need
to solve an inverse problem which is very often ill-posed. This is of great importance especially in regional
modelling. Nevertheless, similar to the arguments given in section 3.1.2, the drawback is that the numerical
integration by means of quadrature rules is limited to the surface of the sphere. This is due to the lack of
appropriate cubature rules for the data above this surface (Schmidt et al., 2007). See Fengler et al. (2005) for
more details of numerical integration methods for data outside the sphere ΩR .
Another alternative to determine the scaling coefficients αk is least-squares adjustment as explained in (3.1.3).
The least-squares estimation of the coefficients αk is mainly similar to the estimation of spherical harmonic
3.3 SH versus SRBF in satellite gravimetry: numerical aspects on the global scale
35
coefficients given by equations (3.31) through (3.42) in section (3.1.3). To evaluate αk using least-squares
method, equation (3.31) should be rewritten in terms of SRBF for band limited observations vi :
NX
K
max
GM X
R
αk
( )n+1 (2n + 1)bn Pn (cos ψ) = vi + ei ,
R
ri
k=1
(3.52)
n=0
where the upper bounds of the summations are restricted to K and Nmax in numerical computations. The
design matrix A will be:
∂V (r)
A=
∂α1
...
∂V (r)
,
∂αk
(3.53)
with
Nmax
∂V (r)
R
GM X
( )n+1 (2n + 1)bn Pn (cos ψ).
=
∂αk
R
r
(3.54)
n=0
Once the design matrix is computed, the least-squares estimation of the scaling coefficients and their covariance
matrix are obtained using (3.36) and (3.42) respectively. In the next section, we describe the procedure
of gravity field analysis using SRBF in more detail. To finish this section, it should be mentioned that the
least-squares process given in section 3.1.3 is applicable in the case that the observations are potential values
(e.g. potential values derived from CHAMP or GRACE data). For other types of observations such as potential
differences dV and line-of-sight accelerometry from the GRACE mission or gravity gradiometry from GOCE
the equations have to be written in terms of first or second order derivatives of the gravitational potential
accordingly. See chapter 2 for more details on the observation equations related to various satellite data.
3.2.2 Relation to spherical harmonics
For the relation between spherical harmonics and SRBF, we make use of the addition theorem given by (3.16)
and put it in equation (3.51)
Nmax
n
K
X
GM X
R n+1 X
V (ri , φi , λi ) =
( )
Ȳnm (φi , λi )
αk bn Ȳnm (φk , λk ).
R
ri
m=−n
n=0
(3.55)
k=1
Comparing equations (3.55) and (3.27), one can write a closed relation between the Stokes coefficients C̄nm
and the scaling coefficients αk :
C̄nm =
K
X
αk bn Ȳnm (φk , λk ).
(3.56)
k=1
This equation shows that spherical harmonic coefficients can be directly computed from the scaling coefficients.
The reverse is not directly possible since it is an under determined inverse problem. Equation (3.56) has
applications when the scaling coefficients αk are to be assessed or to be compared to spherical harmonic
solutions.
3.3 SH versus SRBF in satellite gravimetry: numerical aspects on the
global scale
In this section, we consider the numerical implementation of gravity field analysis on the global scale using
SRBF. The global gravity field will be determined using SRBF with maximum degree Nmax = 70. The
36
analysis is based on simulated potential differences along a GRACE-type orbit, no real data will be considered
here. The reason is, that the focus is on the characteristics of the modelling rather than the field itself. Yet to
be consistent to a good extent, with real data processing, a realistic noise level is also added to the simulated
potential differences along the GRACE orbit. Furthermore, based on these simulated data, the global gravity
field will be determined using spherical harmonics up to degree and order 70, so that it resembles the first
model derived from SRBF. Different aspects of these two analysis methods such as their design and normal
matrices, singular values, condition numbers and the estimated coefficients will be compared. It should be
mentioned that global gravity field modelling using SRBF is not common in practice due to its rather high
computational burden, compared to traditional spherical harmonic analysis. Nevertheless, it gives valuable
insight into regional modelling using SRBF particularly for regularization purposes and this is to be illustrated
in this section. Figure 3.4 shows geoid heights computed using the geopotential model GOCO03s (Mayer-Gürr,
2012) up to degree and order 70. In the following considerations, this gravity field model (in terms of geoid
heights) will be considered as the true field to be reconstructed using spherical harmonics and SRBF.
Figure 3.4: Geoid heights computed from geopotential model GOCO03s. The highest degree and order
included in this expansion is 70. The unit is meter.
3.3.1 Simulated input data and noise
The input data are synthesized potential differences along a GRACE-type orbit. The synthesis is only based
on the geopotential model GOCO03s and no force model, i.e. tides and atmospheric effects, are applied. The
highest degree used in the synthesis is n = 70. The data cover a time period of 30 days with sampling interval of
5 seconds. Thus the total number of samples along the orbit is 518400 data points. To include observation noise
in the modelling, a realization of random noise (white noise) is generated with a realistic standard deviation as
follows: According to Jekeli (1999), the potential difference VAB between two GRACE satellites can be well
approximated by
VAB ≈ kṙA kρ̇,
(3.57)
which is a good approximate for pre-analysis purposes. ṙA and ρ̇ are the velocity vector of the first satellite and
the range rate, respectively. We postulate the error for ṙA and ρ̇ to be in the order of 10−4 m/s and 10−7 m/s,
respectively (Case et al., 2010, Tapley et al., 2004). Applying the error propagation law to equation (3.57), a
realistic noise level for the potential differences along the orbit will be approximately in the order of 10−3 m2/s2 .
Han et al. (2003) also used the same level of noise for their analysis based on simulated data. To avoid being too
optimistic about the noise level, we assume the noise level to be two times larger i.e. 2 × 10−3 m2/s2 . Since the
observation noise is not usually white, the white noise is then used to generate coloured noise by introducing
correlation between adjacent observations. The coloured noise is generated using the following relations
37
c0 = w0
c1 = βc0 +
..
.
p
ci+1 = βci +
1 − β 2 w1
(3.58)
p
1 − β 2 wi+1 ,
where ci denotes the coloured noise based on a realization of the white noise wi . The parameter 0 ≤ β ≤ 1
determines the correlation between adjacent observations which in our simulation, is β = 0.9. This model for
coloured noise is proposed by Grafarend and Vanicek (1980) for the weight estimation in levelling networks
and is also used by Austen and Grafarend (2004) for the recovery of the gravitational field from simulated
GRACE data. Hence, the noisy observations are obtained by adding the coloured noise ci to the synthesized
potential differences VAB .
The result of closed-loop simulation indicate that the imposed noise is realistic and fits to the current accuracy
of GRACE monthly solutions (c.f. figure 3.5).
3.3.2 Global gravity field solutions
The observation equations for both spherical harmonics and SRBF should be written for the potential differences
VAB . According to equation (3.32), the general model in matrix form reads
l + e = Ash xsh = Asrbf xsrbf ,
(3.59)
where Ash and xsh are the design matrix and vector of unknown Stokes’s coefficients for spherical harmonic
analysis. Asrbf and xsrbf are the design matrix and vector of scaling coefficients related to SRBF. The
observation vector l = [v1 v2 ...vI ]TAB consists of potential differences along the GRACE orbit.
Solution 1: Spherical harmonics
The design matrix for spherical harmonics, based on the potential differences, is set up using (3.33) as the
difference between satellites A and B. Since the maximum degree and order included in the series expansion
is 70, the total number of unknowns will be (70 + 1)2 = 5041. Three coefficients, c10 , c11 and s11 , are set
to zero as the coordinate system is assumed to coincide with the Earth’s center of mass (Hofmann and Moritz,
2005). Therefore the number of unknowns will be decreased to 5038. Together with 518400 observations, the
size of Ash and the corresponding normal matrix Nsh = ATsh Ash will be 518400 × 5038 and 5038 × 5038,
respectively.
The unknown coefficients c̄nm and s̄nm are determined using equation (3.36) and their corresponding standard
deviations will be estimated using (3.42). To evaluate global spherical harmonic models, it is common to
illustrate degree standard deviations σn and error degree standard deviations dσn which show the signal and
error contained in each specific frequency (spherical harmonic degree). For this, we computed σn using (3.23)
and dσn using (3.43) which are shown in figure 3.5. In addition, the degree standard deviation using Kaula’s
rule of thumb, given by equation (3.26), was also computed and displayed in this figure. A considerably good
agreement can be seen between degree standard deviations derived from the model and Kaula’s rule of thumb.
To estimate errors in simulation scenarios, it is possible to compute the differences between estimated spherical
harmonic coefficients and coefficients given in the input model (here GOCO03s). These so called empirical
errors can be used to assess the quality of computations as well as simulation:
(
[dcnm ]emp = [c̄nm ]model − [cnm ]goco03s
[dsnm ]emp = [s̄nm ]model − [snm ]goco03s
Figure 3.5 also shows the empirical errors computed from (3.60).
(3.60)
38
The estimated errors are two orders of magnitude larger than the GOCO03s errors. This is however expected
because only one month of simulated data is used to compute this model. Therefore the errors should be
compared to the errors of monthly GRACE solutions which are based on the same period. A good agreement
can be seen between the errors of a GRACE monthly solution and our computations. This agreement is an
indication, that the noise level added to the potential differences along the orbit is realistic.
Figure 3.5: The results obtained from global modelling using a spherical harmonic analysis based on simulated
potential difference along the GRACE orbit; geoid degree standard deviations of the computed
model (thick-blue), degree standard deviations using Kaula’s rule of thumb (dotted-black),
estimated errors given in the model GOCO03s (red), empirical errors of the computed model
(thin-blue) according to input model GOCO03s and errors of GRACE monthly solutions.
Based on the estimated coefficients c̄nm and s̄nm , the geoid heights on the Earth’s surface can be computed
and compared to the GOCO03s geoid. Figure 3.6 shows the geoid difference between the GOCO03s geoid as
shown in 3.4 and the geoid from the estimated model.
39
Figure 3.6: The result of the closed-loop simulation in terms of geoid differences between the global model
GOCO03s and the computed model using spherical harmonics. The differences are in cm level
with a global RMS of about 1 cm.
As it can be seen, the geoid differences are in cm level with largest deviations near the equator. This is due
to the less dense sampling of GRACE-like orbit around the equator. The rms value of the geoid differences is
about 1 cm with minimum and maximum values of −7 cm and 7 cm respectively.
Solution 2: Spherical radial base functions
The design matrix Asrbf will be set up using (3.53) and (3.54) as the potential difference between two GRACE
satellites.
The maximum degree of expansion in equation (3.52) is set equal to 70, (Nmax = 70), to obtain an equivalent
solution to the spherical harmonic case. The Legendre coefficients bn are set equal to 1 since no smoothing
is desired on the global scale. The base functions are distributed on a Reuter grid corresponding to maximum
degree 70 (the Reuter grid is defined in section 4.2.4 ). The number of base functions used in this analysis
are 6207 corresponding to the number of points on the Reuter grid. Thus, the size of Asrbf and Nsrbf are
518400 × 6207 and 6207 × 6207, respectively. Estimation of the unknown scaling coefficients αk on the global
scale is not as straightforward as the Stokes coefficients. The reason roots in the fact that spherical harmonic
functions are (theoretically) orthonormal base functions and therefore are independent. This implies that the
normal matrix Nsh is of full column rank and its inverse in (3.36) can be computed without any difficulty. This
does not hold for Nsrbf due to the dependency of column vectors. The normal matrix Nsrbf belongs to the
class of rank-deficient matrices with dependent columns (and rows). This rank-deficiency has nothing to do
with the observation vector and can be resolved using spectral decomposition of Nsrbf or the so called singular
value decomposition (SVD)1 . Figure 5.4 shows the singular values of Nsrbf and Nsh . As it can be seen, 5038
singular values of Nsh as well as the first 5038 singular values of Nsrbf decay very slowly. There is a sudden
jump between the 5038th and 5039th singular values of Nsrbf . This gap is an indication for the rank-deficiency
of the normal matrix associated with SRBF. This means only 5038 base functions among 6027 base functions
used on the global scale are linearly independent which is equal to the number of spherical harmonics. This
can be considered as a numerical proof that the spherical harmonics and the SRBF span the same function
space.
The solution, i.e. the scaling coefficients αk , are estimated using the truncated SVD method by taking the first
5038 singular values of Nsrbf into account (c.f. section 5.4.1) . Using the estimated coefficients, the geoid
1
See 5.2.2 for more details about the singular value decomposition.
40
heights are synthesized and compared to the GOCO03s geoid. The geoid differences are the same as those
obtained from SH shown in figure 3.6 (to the numerical precision of the used computer).
Figure 3.7 (right) shows the spatial pattern of the estimated coefficients on the corresponding Reuter grid
points. The left panel displays the synthesized geoid using the scaling coefficients αk at the same locations.
Evidently, the scaling coefficients and the geoid heights reveal the same spatial pattern. In other words, the
estimated scaling coefficients look like the geoid or disturbing potential. (compare these two figures also to
figure 3.4. The reason is the space-localizing feature of the SRBF. According to figure 3.3, the energy of these
base functions are concentrated on their centre (the nodes of the grid). Therefore it is expected that the scaling
coefficients are highly affected by the data around their location.
Figure 3.7: Left: The geoid heights computed on the Reuter grid using the estimated scaling coefficients.
Right: The value of the estimated scaling coefficients αk (dimensionless) for each point on the
Reuter grid. According to the space-localizing property of the SRBF, the scaling coefficients
represent the general shape of the geoid. This nice feature can be used as prior information for
regularization purposes. See Chapter 5.
To measure the similarity of the scaling coefficients αk and the geoid heights Nk at locations (φk , λk ), we
computed the cross correlation function using these two signals. The maximum correlation is achieved at zero
lag as expected which amounts to 0.986. The cross correlation function is displayed in figure 3.8. We discuss
this feature with more detail in Section 5.6, where we make use of it as prior knowledge about the unknown
coefficients αk .
Figure 3.8: The cross-correlation function for the estimated scaling coefficients αk and the geoid heights
synthesized at the same locations. The maximum correlation is about 0.986 at zero lag of the
cross-correlation function. The horizontal axis shows the lag of the cross-correlation function.
41
In the previous chapter, we considered the representation of the Earth’s gravity field using spherical harmonics
and the drawbacks of using these global base functions were discussed. SRBF in their general form were
explained. For spherical harmonic analysis, the only parameter which should be chosen, is the highest degree
and order included in series expansion, i.e. Nmax in equation (3.31). The maximum degree is selected based
on the expected frequency content of the input signal or observations. For example the expected maximum
degree of the GRACE monthly solutions is about 120 or for the case of the GOCE static field it is roughly 250.
Once this maximum degree is selected, the design matrix can be set up using (3.33) and (3.34) and the solution
will be obtained. This also holds for global gravity field analysis using SRBF. The reproducing kernel defined
by equation (3.46) is a good choice (and comparable to SH) for global modelling using SRBF and, similar to
SH, only the maximum degree should be chosen. While the mathematical expressions, for global and regional
gravity field modelling using SRBF are rather similar, the numerical implementation differs significantly.
This chapter addresses the use of band-limited SRBF for regional gravity field modelling. The emphasis is put
on satellite-based observations. These base functions are mainly suitable for regional gravity field modelling
and might be considered as complementary approaches to spherical harmonics.
4.1 From global to regional scale
The fundamental difference between the global and regional gravity field modelling using SRBF is, that the
base functions and observations cover only a specific part of the sphere Ω̃R ⊂ ΩR as illustrated by figure 4.1.
We call this region, hereafter, the model zone.
Figure 4.1: From global scale to regional scale; the gravity field is desired on a regional scale within the
subsurface Ω̃R shown by blue frame
To explain this in more detail, we start with equation (3.32) for global modelling and split it as
42
Ax = l + e
=⇒
(
A11 x1 + A12 x2 = l1 + e1
A21 x1 + A22 x2 = l2 + e2
(4.1)
or in matrix form:
A11 A12 x1
l
e
= 1 + 1 .
A21 A22 x2
l2
e2
|
{z
} | {z } |{z} | {z }
x
A
(4.2)
e
l
Assume that the upper left part of the design matrix A, i.e. A11 , is the ’partial’ design matrix, which is set
up for the subregion Ω̃R on the sphere. Correspondingly, x1 ⊂ x and l1 ⊂ l are the unknown parameters and
observation vector within Ω̃R . On a regional scale, we attempt to solve the following equation system
A11 x1 ≈ l1 + e1 .
(4.3)
Equations (3.32) or (4.1) and (4.3) describe the main differences between gravity field modelling using SRBF
on the global scale and regional scales. While the former is a complete setting of the design matrix with global
observations, the latter ignores some components of (4.1) and therefore suffers from ’cutting’ issues. As it can
be seen from (4.1) and (4.3) two ’cutting’ or truncations exist:
• The second line of equation (4.1), i.e. A21 x1 + A22 x2 = l2 + e2 , is completely removed in (4.3). This
equation describes the contribution of l2 (observations outside the region) to the estimation of scaling
coefficients x. Therefore l2 does have effects on the scaling coefficients x1 (coefficients inside the
region). Without the vector l2 modelling the global structures of the geopotential is impossible. In
other words, only the regional part of the gravitational potential corresponding to the spatial extension
of Ω̃R can be modelled and the base functions inside this region can only model the short wavelength
(related to the size of Ω̃R ) of the field. Therefore to solve for x1 , the long wavelengths of the gravity
field must be removed from l1 . In addition, the removal of A21 from the row space of the original design
matrix A is equivalent to cutting the base functions from a certain distance. The reason is that the base
functions are sampled at data points and since l2 is removed, there is no sample from the base functions
at these locations. This is especially a severe problem in borders of Ω̃R which causes edge effects in
the computations. Moreover, those observations which are outside but close to the region Ω̃R , can still
have a considerable contribution to the estimation of scaling coefficients x1 . Therefore it is reasonable
to include more observations beyond the region Ω̃R to reduce the border distortion and effects caused by
the sudden ’cut off’ of the observations. This means the data should cover a larger region compared to
Ω̃R . We call this region, the data zone and denote it by Ω̃data
R .
• Another component which is not considered in (4.3) is A12 x2 . This part models the contribution of the
(removed) scaling functions, x2 , which are outside of the region, to model observations inside the region
i.e. l1 . Removing x2 from the equation system causes another kind of border distortion in computations.
To overcome this problem, it is logical to bring some of the removed x2 back to the equations. Those
elements of x2 which are close to the data zone have significant impact and shall be considered in (4.3).
Therefore the base functions cover another area which we name the grid zone and denote it by Ω̃grid
R .
Based on the discussions above, there are three zones needed for regional gravity field modelling as
data zone
Ω̃grid
R
| {z }
grid zone
z }| {
> Ω̃data
>
R
Ω̃R
|{z}
model zone
(4.4)
4.2 Model setup using SRBF
43
Figure 4.2: Three different zones used in regional gravity field modeling: the model zone (red), the data zone
(blue) and the grid zone (black).
which are illustrated in figure 4.2. Except the model zone which is given by the user, the other two zones
should be defined according to different aspects of the regional modelling. In addition to these two zones,
which should be defined, there are other factors to be predefined for regional gravity field modelling: type
of SRBF and their bandwidth, the number and the position of base the functions, the removal of the long
wavelengths and finally the method of inversion can be mentioned for instance. Therefore, unlike the global
modelling, regional solutions include a collection of different choices to be made. The variety of options in
regional gravity field modelling using SRBF, could be considered as an advantage due to the possible flexibility
in the model setup. Based on the types of available observations and their coverage in a specific region, the
model can be set up for the purpose of the modelling. Most problems mentioned in section 3.1.4 can be handled
using appropriate selections in the model setup using SRBF. On the other hand, if the choices are to be made
arbitrarily or using trial and error, the regional modelling using SRBF becomes a complicated issue with no
clear outcome. In the following section we explain these possible choices in more detail and clarify the way,
the model is set up within this thesis.
Equation (3.51) describes the most general form of gravity field modelling using SRBF. One can rewrite this
equation for regional gravity field modelling as follows:
V (ri , φi , λi ) =
K
GM X
αk
R
k=1
NX
max
n=Nmin
R
( )n+1 (2n + 1)bn Pn (< ri , rk >), i = 1, 2, ..., I
ri
(4.5)
with the spherical distance cos ψ =< ri , rk >. From this equation it is clear that the following factors should
be defined:
1. Shape of SRBF (non band-limited or band-limited determined by bn ).
2. Maximum degree of expansion Nmax which is related to the bandwidth of SRBF.
3. Removal of the long wavelengths (defined by Nmin ).
4. Position of SRBF defined by rk = rk (rk , φk , λk ).
5. Extension of data zone related to I or the number of observations.
44
6. Extension of the grid zone related to K or the number of unknowns.
7. Inversion process or choosing a proper regularization approach.
These different possibilities for the regional gravity model using SRBF have made it almost impossible to
define a unique way to set up the equation system. It is also not easily possible to speak of the best sequence
of choices for all regions and all kinds of data. Due to this diversity, these choices were made arbitrarily using
a specific ’recipe’ in almost all previous works on regional modelling.
There are several research studies where the effect of (some of) these options are considered in a comparison
manner. For example Tenzer and Klees (2008) investigated the choice of optimal SRBF for local gravity field
modelling based on terrestrial data. They concluded that if the depth of SRBF is chosen carefully, different
types of SRBF result in more or less the same accuracy for gravity field modelling. In another study Eicker
(2008) used spherical splines (as a variant of SRBF) to refine the global gravity field modelling based on
satellite data. A main emphasis of her work was to study the impact of different grid types for the distribution
of SRBF on the sphere. In a more general work, Wittwer (2009) presented the applicability of several SRBF for
regional gravity field modelling based on satellite and terrestrial data. He also investigated some aspects such
as bandwidth selection and network design for the position of SRBF. Schachtschneider et al. (2010) included
the effect of satellite altitude, size of the data zone and the degree of the a priori gravity field model in their
research study to investigate the error distribution in regional modelling of the potential and magnetic field.
As an other example, Bentel et al. (2013) compared several band-limited and non band-limited SRBF for gravity
field modelling based on satellite data in a simulation scenario. They discussed the performance of different
SRBF while other choices such as grid type, bandwidth and extension of data and model zones were fixed.
Although such valuable investigations in this field have been carried out, there is yet no reasonable strategy to
define the choices rigorously. Therefore the sequence of choices is usually dependent on the focus of analysis
and is done in an Ad-hoc style. In the followings, we investigate these 7 specifications separately and provide a
guideline for these choices. We try to develop a systematic methodology for the choices to be made which also
maintains the generality of the model setup.
4.2.1 Shape of the SRBF
The shape of SRBF is determined by the Legendre coefficients bn in (4.5). These coefficients act as the
degree-dependent weighting for the Legendre polynomials Pn and control the spectral behaviour of the base
functions. From the signal processing view, the coefficients bn can be considered as the filtering coefficients of
the SRBF and one can tune the regularity of the base functions by modifying these coefficients. Therefore, bn
play an important role also in the inversion of regional gravity field models.
There are several kinds of SRBF depending on how the Legendre coefficients bn are defined. Here we consider
some known SRBF which have been used for the regional gravity field modelling.
The Shannon kernel
The simplest set of coefficients is defined by the Shannon kernel where the coefficients are all one up to a
certain degree. Shannon Legendre coefficients are given by (e.g. Keller (2004))
bsh
n
(
1 n ∈ [0, Nmax )
=
0 elsewhere
(4.6)
which is an ideal low pass (and band pass) filter in the frequency domain. The advantage of the Shannon kernel
is the full control over the frequency content of the base functions since no smoothing is applied.
45
Figure 4.3: Three SRBF with Shannon kernel with Nmax = 60, 120 and 250. The spectral behaviour is shown
in the right panel. This kernel acts as an exact low-pass filter with a sudden frequency cut-off.
The drawback is the rippling of the base functions in the spatial domain caused by the truncation in the
frequency domain, which is analogous to the Gibbs effect in Fourier analysis. This makes the base functions
to have oscillation even in far zones. Nevertheless, as we show in Chapter 6, this shortage can be overcome
by means of an appropriate regularization. Figure 4.3 shows the Shannon-type SRBF with different Nmax as
well as their frequency response. The non band-limited version of the Shannon kernel, is the point mass kernel
which has been widely used in physical geodesy (Vermeer, 1989). It can also be considered as a variant of the
reproducing kernel introduced in equation (3.46).
The Blackman kernel
An alternative to the Shannon Kernel is the Blackman kernel, which was introduced by Schmidt et al. (2006). It
is based on the Blackman window, widely used in signal processing since the 1950’s (Steven, 1997). Blackman
coefficients are


1


n ∈ [0, n1 )

2πn
4πn
bbl
0.42 − 0.5 cos
+ 0.04 cos
n ∈ [n1 , Nmax )
n =

N
N
max
max


0
elsewhere.
(4.7)
Figure 4.4 displays several SRBF with the Blackman kernel. As it can be seen, the spectrum has two parts: a
Shannon-like segment and a transition band to zero. It oscillates much less compared to the Shannon kernel
in far zones. To avoid the smoothing effects of the Blackman kernel in the modelling, n1 in (4.7) should be
46
chosen close to the expected resolution of the desired regional gravity field and Nmax will be rather higher than
n1 (usually twice as n1 ). The consequence of choosing a larger Nmax , will be the need for more base functions
in the analysis. For instance, if in a certain regional gravity field using the Shannon kernel with Nmax = 120,
1500 base functions are needed, the number of Blackman base functions would be about 6000 (four times
larger). The Blackman kernel has been used by Schmidt et al. (2007) for regional gravity field modelling based
on CHAMP data. They used n1 = 80 and Nmax = 192 to model geoid heights in the northern part of South
America.
Figure 4.4: Three SRBF with Blackman kernel with Nmax = 60, 120 and 250. The spectral behaviour is shown
in the right panel. This kernel has a Shannon-like segment and a transition part for smooth decay to
zero.
The CuP kernel
Another kernel is the cubic polynomial or in brief the CuP kernel. It is a polynomial of degree 3 and smoothes
the decay of the power spectrum. Unlike the Blackman kernel, the decay of the power spectrum using the CuP
kernel starts from the beginning. The CuP coefficients are given by

2 
2n
 1− n
1
+
n ∈ [0, Nmax )
bcu
(4.8)
Nmax
Nmax
n =

0
elsewhere.
The spatial and spectral behaviour of the CuP kernel is shown in figure 4.5 for different Nmax . The CuP kernel
filters the frequencies from the beginning which results in much less oscillations in the spatial domain. Nmax
in CuP kernel should be chosen with care to avoid unwanted filtering by the base functions. The CuP kernel
with Nmax = 450 was used by Bentel et al. (2013) along with other types of band and non band-limited SRBF
47
to assess the performance of each base function. They listed the CuP kernel among the base functions which
provide ’very good’ results in terms of residuals on the Earth’s surface.
Figure 4.5: Three SRBF with CuP kernel with Nmax = 60, 120 and 250. The spectral behaviour is shown in
the right panel. The decay of the spectrum starts from the beginning and thus all frequencies are
affected by the kernel.
The Spline kernel
Another way to define the Legendre coefficients bn is to use the frequency response of the Earth’s gravity field.
The degree variances given by equation (3.23) are in fact the frequency response of the gravitational potential
which can be used as the Legendre coefficients. The resulting SRBF are the harmonic splines with the following
kernel
bsp
n


(V )

 σn
= √
2n + 1



0
n ∈ [0, n1 )
n ∈ [n1 , Nmax )
(4.9)
elsewhere
in which, σn are the degree standard deviations from a known model. Alternatively, σn can be computed using
Kaula’s rule of thumb. (V ) can be computed using the error degree variances of a background model or might
be set to zero. Figure 4.6 shows the shape of the spline functions in the spatial and spectral domains in which
(V ) = 0.
48
Figure 4.6: Three SRBF with harmonic spline kernel with Nmax = 60, 120 and 250. n1 is equal to 30 in all
cases. The spectral behaviour is also shown in the right panel. This kernel provides a rational decay
of the spectrum since the Legendre coefficients are computed using the degree variance of a priori
known model or alternatively using the Kaula’s rule of thumb.
Compared to the CuP kernel, the Spline kernel has a logical decay in the spectral domain, since it matches the
nature of the Earth’s gravity field. This approach is proposed by Eicker (2008) for the refinement of globally
determined solutions using regional patches, see also Schmidt et al. (2007) and Eicker et al. (2010). More
details on different kinds of spline kernels can be found in Jekeli (2005).
In this thesis, we distinguish two kinds of SRBF depending on the definition of bn :
• bn = 1 for all n: Such base functions have no measure of regularity since all frequencies have the same
weight.
• 0 ≤ bn ≤ 1 for some n: These base functions contain some built-in regularity since some frequency
parts (often high frequencies) are damped out by bn .
Therefore the Shannon kernel with bn = 1 belongs to the first group while other kernels such as Blackman,
CuP and spline are in the second group. The difference between these two groups of SRBF and their impact in
the regional gravity modelling, can be described in terms of regularization. We will come back to this issue in
section 5.8.
4.2.2 Maximum degree of expansion
The issue of choosing the right Nmax for gravity field analysis is the same for spherical harmonics and SRBF.
This is directly related to the fact that spherical harmonics and SRBF given by equation (3.50), belong to the
49
class of band-limited functions. Band-limitedness of the SRBF implies
bn = 0 for all n > Nmax
(4.10)
so that the expansion can be restricted to the maximum degree n = Nmax . This assumption is true provided
that the signal to be analysed using such base functions, is also band-limited. The observed signals associated
with natural phenomena (i.e. gravitational potential) are rarely band-limited and such assumptions are not
exactly correct. Nevertheless, due to the presence of noise in observations, the signal to noise ratio (SNR) can
be considered as a fair measure to determine the frequency content of a given signal. In case of satellite-based
gravimetry, such as GRACE K-band measurements or GOCE gradiometry observations, the data can be fairly
assumed to be band-limited not only due to the present observation noise, but also due to the signal attenuation
at satellite altitude. Therefore the choice of band-limited SRBF for analysing satellite gravity data is logical
and reasonable. As mentioned before, the expected resolutions for GRACE (monthly) and GOCE solutions are
about Nmax = 120 and Nmax = 250, respectively. These values are valid provided that bn = 1 for all n up to
Nmax . If kernels such as CuP or Blackman are included in the modelling, the Nmax should be chosen carefully
to avoid filtering of the signal components.
For gravity data with high frequency content such as terrestrial gravity observations or airborne gravimetry, it
is still possible to use band-limited SRBF with rather high degree in series expansion. In addition, it is also
possible to use another class of SRBF, known as non-band limited SRBF. In principle equation (3.50) describes
a non-band limited SRBF in terms of Legendre polynomials where the maximum degree is not bounded. To
apply such functions in gravity field analysis, the analytical expressions should be available. Klees et al. (2008)
summarizes the analytical form of several non-band limited SRBF such as point mass kernel, radial multipole
and Poisson wavelet. The point mass kernel has probably the simplest analytical form as it is the reciprocal
distance between evaluation points and the location of base functions. Many investigations have been carried
out to model gravity fields using point masses. Tenzer and Klees (2008) address a rather complete list of
research studies using non-band limited kernels.
In this thesis we restrict our investigation to band-limited SRBF since the goal is to analyse satellite based
observations.
4.2.3 Removal of the long wavelengths
The Earth’s gravitational potential consists of all frequencies and wavelengths. The long wavelengths correspond
to global features of the field and the short wavelengths reveal the regional and local properties. The recovery
of all components is only possible on the global scale where global observations are available. This means
that on regional scales the long wavelengths, i.e. the global components, cannot be determined. Therefore the
expansion (4.5) should be limited to short wavelengths according to the size of the model zone. Hence, while
Nmax is chosen due to the frequency content of the observations, Nmin is dependent on the size of the region
or the model zone. The relation between the spatial wavelengths of the region and corresponding degree of SH
or SRBF is given by an approximate rule of thumb:
n=
40000
w
(4.11)
in which w is the size of the region in km and the equatorial perimeter of the Earth is approximately set to
40000 km. This equation gives an insight into the right Nmin in (4.5). For example if the size of the model
zone in figure 4.2 is about 1500 km, the wavelengths n < 26 cannot be determined correctly and will corrupt
the estimation. Hence it is reasonable to set Nmin = 26 or larger.
Restriction of Nmax and Nmin to certain values means that the resulting SRBFs act as band-pass filters
provided that the scaling coefficients αk are obtained via convolution. However, since parameter estimation
is performed using the least-squares adjustment, the (regional) observation vector l1 should also be reduced to
avoid the leakage of the long wavelengths to the regional solution. In other words, the long wavelengths of
the gravitational potential must be removed from the observation vector l1 . This implies that the observations
vector l1 need to be reduced with synthesized pseudo observations based on a prior gravity model up to Nmin :
50
min
δl1 = l1 − lN
1
(4.12)
min
This reduction makes the regional solution being dependent on the prior model used to synthesize lN
. One
1
can also consider the regional solution to be a regional refinement for this prior model; less refinement is
needed for big Nmin and vice versa more refinement is needed for smaller Nmin .
As stated before, Nmin can be obtained from equation (4.11) so that the observations are reduced as little as
possible and consequently the final regional model will be less dependent on the prior model. In some research
studies, the authors used the maximum reduction of the observation vector. In this case the prior global model
plays a central role in the final modelling and the regional solution is responsible for very tiny refinement to the
global model. See for example Eicker (2008), Antoni (2012) and Tenzer and Klees (2008). In these studies, the
idea is to first model the gravitational potential using spherical harmonics with the maximum possible degree
Nmax . In the next step, the residuals will be ’regionally’ re-analysed using space-localizing base functions.
This is also a common method in global gravity field modelling. The difference is that, in global gravity field
modelling, the corrections to the removed part will also be estimated so that the reference field is updated. In
contrast, in regional gravity field modelling, the removed part is considered as the true field which will be added
to the regional solution.
In our methodology, we prefer to model the regional gravity in a way, that the SRBF have the maximum
contribution. In other words, we reduce the observation using the minimum possible Nmin so that the final
regional solution is less affected by the input global model. In the numerical investigations in Chapter 6, we set
Nmin = 30 according to the size of the selected test regions. Choosing a larger Nmin is unnecessary since no
remarkable improvement is seen.
4.2.4 Position of the SRBF
Another important choice to be made for gravity field analysis using SRBF is the location of base functions
where they are centred. The position vector of base functions is needed for the evaluation of Legendre
polynomials Pn (cos ψ) as it depends on the location of data (evaluation points) and the base functions, see
equation (3.17). There are generally two ways to determine the location of base functions:
Free-positioned base functions
In this method the position of the base functions is to be determined within the parameter estimation along with
unknown scaling coefficients. Thus a non-linear problem with three parameters for each base function (two
parameters for the position and one as for the scaling coefficient) has to be solved for. This reduces the number
of SRBF significantly which is an advantage. The cost, however, is to pose additional unknowns and including
non-linear parameters in the equations system which consequently results in more complexity of the gravity
field analysis. Antoni (2012) developed a non-linear approach to determine the position of base functions
simultaneously with scaling coefficients. Alternative approaches to reduce the number of base functions have
been also proposed. Klees et al. (2008) and Wittwer (2009) presented a data-adaptive strategy to reduce the
number of base functions. Some authors describe the position of base functions in 3D space where the depth
of the base functions is also an important choice to be made. For majority of SRBF used in gravity field
modelling, the choice of depth is equivalent to bandwidth selection of SRBF (Klees et al., 2008), see also
Marchenko (1998), Marchenko et al. (2001) and Marchenko (2003) for more optimization algorithms to reduce
the number of base functions in a free-position manner.
Fixed-position base functions
A very common way to define the location of base functions is to use fixed positions. In this method a cluster
of points, called grid points, should be distributed on the surface of the sphere. Since SRBF are symmetric
and isotropic base functions, the grid points are also expected to be distributed as homogeneous as possible.
The number of grid points, i.e. the number of base functions, must not exceed the total number of observations
(I ≥ K). Moreover, the distance between grid points should be such that the adjacent base functions cover
the region in between reasonably. This is directly related to the width and therefore to the highest degree
(Nmax ) included in series expansion (for band limited SRBF). The higher the Nmax is, the narrower the base
51
function will be and consequently more base functions are needed. Eicker (2008) summarized and presented
several kinds of point distribution on the sphere, such as Driscoll-Heal grid, Triangle vertex, Triangle centre and
Reuter grid and discussed the characteristics of each in detail. In another study, Gonzalez (2010) introduced
a homogeneous point distribution on the surface of the sphere, known as the Fibonacci grid. The goal was to
reduce the errors related to the measurement of the Earth coverage of satellite constellations.
Compared to free-positioned base functions, a disadvantage of fixed-position base functions is, that the base
functions are more correlated. This causes more ill-posedness in the equation system and the associated design
matrix. Nevertheless, the induced ill-posedness is not a serious concern since it can be treated by means of
proper regularization.
Our computations show that the choice of grid points does not considerably change the quality of regional
gravity field modelling, provided that the grid points are homogeneously distributed. For example, the standard
geographical grid with equal angles, does not provide satisfactory homogeneous point distribution on the
surface of the sphere. This is due to the convergence of meridians especially in high-latitude regions.
In this thesis we use the fixed-position approach to predefine the location of base functions so that the parameter
estimation using least-squares adjustment remains linear. We will compare the performance of two homogeneous
grid points: the Reuter grid and the Fibonacci grid. A brief mathematical description of these two grid points
is given in the following for the sake of completeness.
The Reuter grid
The concept of the Reuter grid is to distribute the grid points on the surface of the sphere in a way, that the
distance between adjacent points is equal. The distance between points as well as the total number of grid points
is defined by the control parameter c. This parameter determines the number of points along the meridians. The
number of points on each circle of latitude will be computed according to its latitude and the distance to the
adjacent circles. Based on the parameter c, the position of the points on the Reuter grid can be obtained as
follows:
(
φj = jπ/c, j = 1, 2, ..., c − 1
λij = 0.5∆λj + 2πi/cj , i = 0, 1, ..., cj
where c is the control parameter and cj and ∆λj are computed using:

2π


c
=
 j
∆λj
cos(π/c) − cos2 φj


.
∆λj = arccos
sin2 φj
(4.13)
(4.14)
It should be mentioned that the two poles are not computed using (4.13) and must be added manually. See also
Reuter (1982), Eicker (2008) for a more detailed description on the Reuter grid. The number of grid points,
which is controlled by c is directly related to the band width of the base functions of Nmax . The larger Nmax is
the more base functions are needed for a proper coverage. Figure 4.7 shows the distance between the adjacent
base functions on two different Reuter grids corresponding to c = 30 and c = 120. As it can be seen the base
functions get closer as the bandwidth decreases. The global distribution of the Reuter grid points for these two
cases is shown in figure 4.8.
52
Figure 4.7: Left: the distance between adjacent base functions on the Reuter grid corresponding to base
functions with Nmax = 30. Right: the distance between adjacent base functions on the Reuter
grid for base functions with Nmax = 120. As the maximum degree increases, the base functions
will be more localized and should get closer.
Figure 4.8: The distribution of points on the Reuter grid for Nmax = 30 (left) with a total number of 1290
points and Nmax = 120 (right) with 20798 points.
The Fibonacci grid
The points on the Fibonacci grid approximately provide equal areas on the surface of the sphere. According to
Gonzalez (2010), the spherical coordinates of the Fibonacci grid, in radians, are

2i

φi = arcsin
2N + 1
2πi

√
λi =
(1 + 5)/2
(4.15)
where i = −N, ..., 0, ..., N and N is an integer such that the total number of Fibonacci points is 2N + 1. Every
point of this grid is located at a different latitude with the middle point
i = 0 placed at equator. The interesting
√ !
1+ 5
, in equation (4.15).
fact about the Fibonacci grid is the use of the golden ratio,
2
53
(a)
(b)
Figure 4.9: Global and homogeneous point distribution on the surface of the sphere, (a): The Fibonacci grid
with equal areas and (b): The Reuter grid with equi-distant intervals. The total number of points
in both grids are tuned to be 317. As it can be seen, the points on the Reuter grid are placed on 15
different circles of latitude while the Fibonacci grid has a pseudo-random distribution.
Figure 4.9 shows globally distributed grid points on the Reuter grid with c = 16 and a total number of 317
points. In addition, a Fibonacci grid with N = 158 is also shown. The total number of Fibonacci points is
again 317 which is comparable to the Reuter grid.
4.2.5 Extension of the data zone
As we explained in section 4.1, in regional gravity field modelling, the observations are restricted to a certain
region which causes severe border distortions in regional gravity modelling. The reason is obvious due to the
fact that the Earth’s gravitational potential is a function of mass distribution all over the globe. This means that
the potential field in the model zone Ω̃R affects the observations outside this area. As explained in 4.2.3, the
removal of the long wavelengths from the observation vector l1 can overcome this problem considerably. Thus
the regional potential field can be determined based on the observations within this region. Nevertheless, those
observation which are close to the model zone can still have significant contribution to the estimation of scaling
coefficients x1 . Therefore the data zone Ω̃data
is introduced to reduce the edge effects. The data zone cover a
R
broader area beyond the model zone in a way that the adjacent observations to the model zone are also included
in the parameter estimation, see figure 4.2.
The extension of the data zone is usually chosen arbitrarily using trial and error and has not been investigated in
previous studies. The trial and error is done in a sense that a satisfactory fit in model zone is achieved. Though
the extension of the data zone is not a very critical issue in regional gravity field modelling, we consider it here
and give a rule of thumb for the size of the data zone.
According to equation (4.12), the observations are reduced based on a reference field. The resulting observation
vector δl1 consists of frequencies between Nmin + 1 up to the expected maximum degree. The extension of the
data zone can be determined based on the longest wavelengths in the observations i.e. Nmin + 1. The lowest
spatial resolution contained in δl1 , can be determined by
20000
km
Nmin
(4.16)
2 × 107
rad
Nmin × R cos φm
(4.17)
Rmin =
or in radians using
Rmin =
where φm is the average latitude of the region. This gives the minimum spatial resolution at the Earth’s surface.
For satellite observations at altitude h it can be written as
54
Rmin =
2 × 107
rad.
Nmin × (R + h) cos φm
(4.18)
The extension of the data zone beyond the model zone, can be considered as the half of the minimum spatial
resolution i.e. 0.5Rmin . Therefore the bounds of the data zone is obtained using the model zone extended in
all directions by 0.5Rmin . For example, for a regional solution using GOCE data with h = 250 km over a
region with average latitude of 50◦ , the extension to model zone will be about 4.5◦ if the long wavelengths are
removed up to Nmin = 30.
As it can be understood from equation (4.18), the size of the data zone is dependent on the frequency content of
the reduced observations as well as satellite altitude and, of course, on the size of the model zone. Therefore,
the data zone is defined based on the features of the observations. It should also be mentioned that equation
(4.18) suggests the minimum required extension for the data zone. More extension results in involving more
observations in the equation system and consequently better solutions with reduced border effects. The cost
will be to deal with a larger equation system and computation time.
4.2.6 Extension of the grid zone
Another area which should be defined is the grid zone. As explained in 4.1, this area is larger than the model
and data zones. The grid zone is considered as the extension of the data zone. Similar to the discussion about
the data zone, this area has also been selected arbitrarily in previous research studies. Here, we relate the size
of the grid zone to the properties of the SRBF. The maximum resolution of the SRBF is dependent on the
maximum degree of expansion in equation (4.5). Using (4.17) the maximum resolution of SRBF is
Rmax =
2 × 107
rad.
Nmax × R cos φm
(4.19)
The base functions outside the data zone which are close to this area have significant contribution in the
modelling. Therefore, the grid zone is defined as the extension of the data zone. In our methodology, we
define this extension to be equal to the maximum resolution of the base functions used in the analysis. This is
illustrated in figure 4.10.
Figure 4.10: The extension of the grid and data zones with respect to the size of the model zone to reduce border
distortions. The base functions are distributed within the grid zone where the unknown coefficients
are determined. The observations are provided in data zone.
55
Again it should be noted that equation (4.19) gives the minimum value needed for the extension of the grid
zone. Larger extension seems to be unnecessary since the number of unknowns and the size of computations
will be increased as the result. Our computations show that a grid extension between 3 and 5 degrees should be
satisfactory for gravity field modelling based on satellite data.
4.2.7 Inversion process
When all choices are made, one can set up the observation equation defined by (4.3). According to the
presence of errors, the resulting observation equations are strongly inconsistent. The errors in the model can be
categorized to three different groups:
• Commission error: The observation noise propagates to the estimated unknown coefficients through the
linear model which is called the commission error. This kind of error is present in all types of modelling
based on observed values.
• Omission error: This error is due to the restriction of the modelling to the maximum degree of expansion.
In principle the gravity field of the Earth is a non band-limited function which contains infinite frequencies.
The omission of higher frequencies beyond Nmax causes the omission error in the final solutions. This
type of error exists also in global gravity field modelling since the expansion of spherical harmonics is
also restricted to a certain maximum degree.
• Cut-off errors: This error source is the result of regional confinement. According to the discussions in
section 4.1 in the context of equations (4.1) and (4.3), the regional gravity models suffer from cutting
issues which have to be taken into account.
The last group of errors is a special case for regional gravity field determination which does not exist in global
gravity field modelling. Therefore the resulting equation systems in regional gravity field modelling is much
more ill-posed compared to global gravity field modelling. This means the estimation of scaling coefficients
αk is not easily possible using the standard least-squares adjustment and should be done by means of special
treatments. Additional information should be included to obtain meaningful results. Such special treatments,
known as regularization, are the most important part of regional gravity field modelling which should be taken
into account carefully.
From the view point of signal processing, the regularization process can be compared to the act of averaging
and low-pass filtering. Therefore it is possible to consider the regularization procedure, equivalent to applying
a low-pass filter to the solution where the goal is to hamper the propagated errors to the solution. The
regularization process, which is the central issue of this PhD thesis, will be studied in the following chapter
with more detail.
57
5 Regularization of regional gravity field
solutions
5.1 Gravity field modelling: an inverse problem
The gravity field recovery from observed gravity data belongs to the class of inverse problems. Inverse
problems exist in many fields of applied sciences with the following common concern:
The characteristics of an underlying process (phenomenon) are to be determined from a set of noisy
observations.
An inverse problem consists of three components; input, underlying process and output. These components
are named in the view of forward modelling. Outputs of a process are always observable and can be measured
accordingly. From the underlying process and input, one is usually given and the other is unknown. Figure
5.1 illustrates the forward problem and its associated inverse problem in a general form. In the context of the
gravity field modelling, these three components can be defined as follows:
• Process: The gravity field of the Earth, as a continuous function, is the process of the problem. Since
this process is not known, we attempt to approximate it using a set of known functions (base functions).
Therefore, the approximating model includes a set of known base functions (e.g. spherical harmonics or
SRBF) which together with their corresponding coefficients (inputs) construct the output.
• Input: the coefficients of a set of known base functions.
• Output: The gravitational potential and/or its functionals, at certain position and time. The output as
the realization of the process can always be observed using measurement techniques (e.g. gravimetry,
gradiometry, SST, SGG, etc).
Figure 5.1: The forward and inverse problem and corresponding components. In the context of the gravity field
modelling, the process is the gravity field of the Earth, the output are the observations and the input
are the unknown coefficients to be estimated.
Many inverse problems take the form of Fredholm integral equation of the first kind. Such problems arise
in many field of applied sciences such as medical imaging, astronomy, geophysics and in particular geodesy.
The general form of this integral equation reads (Hansen, 2010):
58
Z
K(s, t)x(t)dt = l(s)
(5.1)
Ω
in which K(s, t) describes the process and x(t) is the input function at time or position t. The function l(s)
at time or position s is the output or the observations of the process. (5.1) describes the inverse problem in the
continuous real world. In the discrete numerical computations, this integral equation can be written in terms of
matrix notation:
Ax = l
(5.2)
which resembles the equation systems for global or regional gravity field modelling given in chapters 3 and 4.
The matrix A : X → L is a linear operator or a mapping from the unknown space X to the observation space
L. A describes the process in discrete form. Respectively, the unknown vector x ∈ X and observation vector
l ∈ L are the input and output of the process. This is shown in figure 5.2.
Figure 5.2: The operator A is a mapping from function space X of unknowns to the observation space L
The mapping A is said to be well-posed if it has the following properties (Hadamard, 1923):
• A is surjective: the solution x exists for every right hand side l (existence).
• A is injective: for every right hand side l, there is only one solution x (uniqueness).
• A−1 exists and is continuous (stability).
A−1 is the inverse mapping from space L onto X such that1
x = A−1 l.
(5.3)
If one of theses conditions does not hold, the operator A is said to be ill-posed and the solution (5.3) cannot
be reliable. In the context of the Earth’s gravity field, A is never surjective in a strict mathematical sense.
This implies that there is no exact x which satisfies equation (5.2). The reason is due to the redundant noisy
observations which makes the equation system (5.2) inconsistent. Nevertheless, the existence issue can be
resolved by introducing additional requirement for the solution. The least-squares method explained in chapter
3, is a condition that guaranties the existence of a solution for (5.2). According to the least-squares assumption,
the approximate solution x̂ (instead of the exact solution x) exists such that kAx̂ − lk is minimized. Thus, the
issue of existence is not a great concern in gravity field modelling since we look for a good approximation
rather an exact solution.
1
Note that A is not a matrix here. It denotes a continuous linear operator. Consequently A−1 is not a matrix inverse, rather the inverse
projection or inverse mapping in the continuous sense.
5.2 Diagnosis of ill-posedness in inverse problems
59
Presence of different errors (i.e. observation noise and systematic effects) in the modelling is a limiting
factor for the uniqueness of the approximate solution. As a result of the least-squares assumption (or any
other requirements to obtain an approximate solution), injectivity of A and therefore the uniqueness of the
solution are vague notions and shall be predefined. The reason is that, there might be several good approximate
solutions for a given set of observations depending on how the errors are minimized. Under certain conditions,
one can speak of the best approximation instead of the unique solution. The best approximation is defined
depending on the purpose of modelling and its applications. For example the approximate solution obtained
from least-squares method can be considered as the best approximation if minimum variance for the solution
is desired. This can be achieved if the weight matrix in the least-squares solution is chosen to be inversely
proportional to the covariance matrix of the observations.
For global gravity field modelling, the injectivity of A is a convenient assumption according to the properties
of least-squares solution. In section 3.3.2, the solutions x̂sh and x̂srbf (which were shown to be equivalent) are
considered as the best approximation. On the contrary, in regional gravity field modelling, A is not injective
even under assumption of the least-squares and several solutions might fulfil the minimum norm condition.
We will come back to this issue later in section 5.4, in the explanation of figure 5.5. This is mainly due to
the restriction of (globally defined) base functions and observations to a certain region. Hence, additional
requirements for the desired solution x̂ are necessary to obtain a measure for the best approximation.
Finally, the inverse problems are instable. Instability implies that the solution x does not continuously depend
on the observation l. The reason is, that the kernel K(s, t) of Fredholm integral equation of the first kind has
smoothing effects on the input f (t) so that the output g(s) (observations) are smoother than the input (source).
This holds also for the discrete version of this integral equation; the operator A has smoothing effects on x so
that l is smoother than x. Smoothing effect in forward modelling causes instability in inverse problem. This
phenomenon can be mathematically described by Riemann-Lebesgue lemma (Hansen, 2010):
If f (t) is a function defined as:
f (t) = sin(2πωt), ω ∈ [1, ∞)
(5.4)
it can be shown that
Z
K(s, t)f (t)dt → 0 as ω → ∞
g(s) =
(5.5)
Ω
for any arbitrary kernel K. This explicitly means that as the frequency of the input (source) increases, the
amplitude of the output (observation) will be damped out. Therefore in the inverse problem higher frequencies
cannot be determined as precise as lower frequencies, particularly in presence of observation noise. In this case,
the inverse operator A−1 (if exists) is not stable so that x is not continuously dependent on l. This damping
effect is even more intensified in gravity field modelling based on satellite data which is known as the upward
continuation.
To resolve the instability of A, additional information about the unknowns is required to constrain the solution
x̂. This procedure is called regularization so that the instable operator A becomes regular.
In previous section we explained that the operator A is ill-posed and a reliable solution can be obtained only by
means of regularization. But before ’curing’ this ill-posedness, the reason and the extent of ill-posedness shall
be ’diagnosed’ in a proper way. We often know that the resulting operator A (design matrix) could be ill-posed
due to the characteristics of the modelling but usually the extent to which the design matrix is ill-posed is not
known. In practice, there are some tools to check whether an operator is ill-posed and if it is, to which extent.
These tools will be explained in the following.
60
5.2.1 Condition number
An important property of the operator A, which shows the degree of ill-posedness, is the condition number.
The condition number of A is defined as (e.g. Cheney and Kincaid (2008), Higham (1987)):
cond(A) = kAkkA−1 k
(5.6)
where kAk and kA−1 k denote the norm of A and its inverse respectively1 . Condition number is a good measure
for the sensitivity of the operator A to the errors in the observations. If observation error and the solution error
are denoted by e and δx respectively, one can write:
A(x + δx) = l + e
(5.8)
or in other from:
(
l = Ax
δx = A−1 e
(5.9)
Taking the norm of both equations and due to the properties of the operator’s norm (e.g. Kreyszig (1978) page
92)
(
klk = kAxk ≤ kAkkxk
kδxk = kA−1 ek ≤ kA−1 kkek
(5.10)
Combining these two inequalities yields:
kδxk
kek
≤ kAkkA−1 k
| {z } klk
kxk
(5.11)
cond(A)
Equation (5.11) states that the relative errors δx can be amplified up to level of observation’s errors multiplied
by cond(A). If cond(A) is close to one or small enough, then the observation errors, e, will not be amplified
significantly so the operator and thus the system of equations are said to be well-posed or well-conditioned. A
large condition number results in much more error propagation and reveals more ill-posedness in the operator
A. Hence more treatment (regularization) is needed to obtain a reasonable solution.
5.2.2 Singular value decomposition
A powerful tool to find out difficulties associated with ill-posed operators, is the Singular Value Decomposition
or, hereafter, SVD. It is a well-known numerical tool to reveal some characteristics of ill-posed matrices (Gloub
and van Loan, 1996, Hansen, 1997, 2010). SVD belongs to the family of matrix factorization and is connected
to the spectral theory of linear operators. The SVD of a linear operator A ∈ RI×K reads:2
A = USVT =
K
X
uk sk vkT
(5.12)
k=1
1
The L2 -norm of a matrix, in a simple form, is defined as follows:
kAk = max{kAxk such that kxk = 1}
2
Kreyszig (1978) gives a detailed description of the norm of linear operators in general.
RI×K is the space of all linear operators whose dimension is I × K.
(5.7)
61
where U ∈ RI×I and V ∈ RK×K are orthonormal matrices with orthonormal column vectors uk and vk such
that:


kuk k = kvk k = 1



UT = U−1

VT = V−1



UT U = UUT = VT V = VVT = I
(5.13)
The diagonal matrix S ∈ RI×K contains non-negative values sk which are the singular values of A and appear
in decreasing order such that:
s1 ≥ s2 ≥ s3 · · · ≥ sK ≥ 0
(5.14)
If one or more singular values are equal to zero, the matrix A is not of full column rank and is said to be rank
deficient. Using equation (5.12), one can write:
Avk = sk uk
(5.15)
According to the definition of the matrix norm and using (5.15) it can be shown that:
kAk = s1
(5.16)
where s1 is the first and, by definition (5.14), the largest singular value of A. Furthermore, it is straightforward
to show that:
A−1 = VS−1 UT
(5.17)
kA−1 k = s−1
K
(5.18)
and consequently:
with sK being the last and smallest singular value of A. Using (5.6), (5.16) and (5.18) the condition number of
A can be obtained as the ratio of the largest singular value to the smallest:
cond(A) =
kAk
s1
=
sK
kA−1 k
(5.19)
Since the approximate solution x̂ is to be obtained using least-squares method, it is convenient to write the
equation (5.8) in the level of normal equations:
Nx = y
(5.20)
in which N = AT PA and y = AT Pl are defined in the context of equation (3.37). In terms of operator
equations, N : X → Y can be considered as a linear operator which maps the vector x from unknown space X
onto its dual space Y (Mohammad-Karim, 1981). Hence, it makes more sense to consider the condition of N
rather than A. Since N is a symmetric matrix, its SVD is equivalent to eigenvalue decomposition (Strang and
Borre, 1997):
62
eigenvalue decomposition
z }| {
QΛQT
T
N = Ṽ
| S̃{zṼ } =
(5.21)
SVD
therein Ṽ is an orthonormal matrix and S̃ is a diagonal matrix with singular values s̃2 on its diagonal. Q
contains the eigenvectors of N and Λ is a diagonal matrix with eigenvalues λ on its diagonal.
A special case (as often occurs in practice) is when P = σ 2 I and thus N = σ 2 AT A. Then using (5.12) and
(5.13) one can write:
T
N = σ 2 AT A = σ 2 VS |U{z
U} SVT = σ 2 VS2 VT
(5.22)
I
which gives the singular value decomposition of the normal matrix N in terms of SVD components of A. It
also follows that in this case (P = σ 2 I) the singular values of A are the squared root of the eigenvalues of the
corresponding normal matrix. In the following we assume that P = σ 2 I and therefore use (5.22) as SVD of N
unless otherwise stated.
With the same line of reasoning for the condition number of A ( equation 5.19), the condition number of N
can be estimated by means of its singular values or equivalently by its eigenvalues:
cond(N) =
kNk
s2
λmax
= 21 =
−1
kN k
λmin
sK
(5.23)
According to (5.22) and using (3.36), it is straightforward to show that the least-squares solution x̂, in terms of
SVD components reads:
x̂ = VS−2 VT y
(5.24)
which replaces the inversion of N by inversion of a diagonal matrix S2 i.e. inverting the singular values s2 .
The singular value decomposition is analogous to the Fourier transform in a sense that it reveals the spectral
properties of the linear operators (or matrices) (Hansen, 2010); Large singular values correspond to long
wavelengths (low frequencies) and small singular values represent the high frequency characteristic of the
operator. The SVD enables us to determine the significance of different frequencies for the mapping.
From viewpoint of functional analysis, the column vectors of A and similarly N, constitute a base (say a
K-dimensional coordinate system for simplicity) for the function space X. The unknown vector x is to be
measured in this coordinate system. This base is chosen by the user according to the nature of the problem and
desired application.
Figure 5.3: Two coordinate systems for studying the object abc. The coordinate system pqr is defined locally
according to properties of abc.
5.3 Ill-posedness of gravity field determination
63
As in gravity field modelling, we chose SRBF due to its benefits explained in chapters 3 and 4. Nevertheless, as
the choice of base functions is mostly physically reasonable, it might not be always computationally efficient.
An abstract and simple example is illustrated in figure 5.3. If the object abc is to be investigated on a 2D plane,
it is common to use the Cartesian coordinate system XY which enjoys the features of orthogonality. Yet, for
studying some properties of this object (e.g. the slope of its sides), it is perhaps preferred to define a local
coordinate system such as pqr which fits better to the geometry of abc since its axes are defined parallel to
abc’s sides. The slopes of ab, bc and ac are now zero with respect to the localized axes p, q and r respectively.
While this can be regarded as an advantage of this localized coordinate system, the drawback is the loss of
orthogonality of axes (bases) and consequently the Euclidean geometry is not valid any more. In addition, three
axes are linearly dependent on a 2D plane which cause dependency and rank-deficiency in the operator which
describes the base pqr. This example mimics how spherical harmonics as XY and SRBF as pqr look like in
gravity field analysis.
SVD can be considered as a coordinate transformation in the function space X from system defined by column
vectors of A or N to an orthonormal base defined by column vectors of V. In other words, SVD is a transition
to an interim orthogonal coordinate system for efficient computations.
The magnitude of singular values exhibits the significance of vk as the axes of this orthonormal base. This is
how SVD together with condition number can be worthwhile to detect the ill-posedness of operators and give
insight into the proper treatment. In section 5.4.3 this issue will be considered with more details.
5.2.3 Discrete Picard condition
Another tool to detect the ill-posedness of the equations is the discrete picard condition which is closely
connected to SVD. This condition also describes the effect of observation errors on the solution. Equation
(5.24) which describes the least-squares solution based on SVD components, can also be written as the linear
combination of orthonormal vectors vk :
x̂ =
K
X
vT y
k
k=1
s2k
vk
(5.25)
As it is clear from this equation, the solution x̂ converges if the ratio vkT y/s2k is convergent. This requires that
the coefficients vkT y in the nominator are smaller than the singular values s2k on average. If this condition is
violated, the ratio vkT y/s2k diverges so does the solution x̂. Hansen (1990a) described this condition as the
discrete Picard condition which states that the coefficients vkT y decay on the average to zero faster than the
singular values s2k . See also Hansen (1997, 2010) for more details on the discrete Picard condition.
5.3 Ill-posedness of gravity field determination
To see how SVD and condition number can reveal the ill-posedness of normal equations in gravity field analysis,
we consider the normal matrices used in section 3.3.2, for global gravity field solutions.
Figure 5.4 shows the singular values of the normal matrices computed from Nsh and Nsrbf . The solutions
obtained from these two normal equations were shown to be equivalent in section 3.3.2. Now a closer look
at the corresponding singular values shows this clearly. There are 5038 and 6200 singular values for Nsh and
Nsrbf corresponding to the number of unknowns in each case. As it can be seen from figure 5.4, the singular
values s2srbf show the same behaviour to s2sh up to the 5038th singular value. A sudden jump after this point
exhibits the dependency of column vector and thus the rank deficiency in Nsrbf as discussed in section 3.3.2.
Ignoring the singular values after sudden jump, the condition number of Nsh and Nsrbf will be the same:
cond(Nsh ) = cond(Nsrbf ) = 1.376 × 105
(5.26)
A condition number in the order of 105 , is not a real problem for today’s computers so that the the normal
matrices with such condition numbers can be inverted without difficulties.
64
(a)
(b)
Figure 5.4: (a) Singular values of the normal matrices Nsh (black) and Nsrbf (blue) described in 3.3.2 for
global gravity field modelling; the sudden jump between 5038th and 5039th singular values reveals
the rank deficiency of Nsrbf and is the truncation point for TSVD solution. The singular values
before sudden jump span approximately 5 orders of magnitude and have the same behaviour as the
singular values of Nsh . (b) Singular values for the ill-posed problem resulting from regional gravity
field determination described in section 6.2.2; these singular values with rapid decay, span about 18
orders of magnitude.
To judge whether the condition number of a matrix is normal or large (i.e. whether regularization is necessary or
not), it is good to know a measure of this number. For gravity field analysis the expected condition number can
be approximately estimated based on Kaula’s rule of thumb explained before. This is used in many gravity field
solutions as a pre-conditioning of the normal matrix to stabilize the solution. Figure 5.4 also shows the singular
values of the normal matrix N11 obtained from a high-resolution regional solution (nj = 255) using SEBF.
The condition number is now in the order of 1018 which shows a strong ill-posedness of the normal matrix. The
reasons of such ill-posedness are not only those coming from observations and downward continuation (as in
global case) but also due to the incompleteness of the mathematical model, discussed in chapter 4. A reliable
solution for such regional models can be obtained only by means of a proper regularization method. Hence, the
regularization for regional gravity field solutions should resolve the following problems simultaneously:
• the non-stability of the inverse operator N−1
11 due to presence of errors and issues such as the downward
continuation and
• the non-injectivity of N11 according to discussions in chapter 4.
See also the discussions concerning different sources of errors in section 4.2.7.
5.4 Regularization of ill-posed problems
Due to equation (5.25) which gives the least-squares solution in terms of SVD components, singular values
equal to zero or very small singular values are the source of instabilities in the solution and shall be filtered
out. Therefore, once the SVD components are computed, it is necessary to evaluate which singular values
are significant and which ones cause instability (due to their small values). Small singular values will have a
large contribution in the inversion process using equation (5.25). This means the column vectors of vk which
correspond to small singular values, can artificially contribute to the solution x̂ so that not only the magnitude
of x̂k changes, but even their signs. Therefore the trivial (small) singular values shall be either removed or
filtered out so that their contribution smoothly decay. To do so, there must be a measure to determine the
significance of singular values. This is key point and indeed the crux of regularization of ill-posed problems.
Since there are no rigorous criteria for that, there are several regularization methods in practice. Xu (1998)
gives an overview of several truncated SVD methods for discrete linear ill-posed problems and compared them
65
for a regional gravity field determination using Stokes’ kernel. Regularization of ill-posed problems can also be
performed without using SVD or any other decomposition tools. Such regularization approaches belong to the
class of Tikhonov regularization (Tikhonov and Arsenin, 1977) and can be considered as direct regularization
methods. Nevertheless, the Tikhonov-type regularizations can also be expressed in terms of SVD components
and introducing filter factors (Hansen, 1997). In this PhD thesis, we categorize two types of regularization:
• Truncated SVD (TSVD)
• Tikhonov regularization (weighted SVD)
In the following we investigate these two classes of regularizations for ill-posed problems and put emphasis
on the regional gravity field solutions using SRBF. We also propose a heuristic approach to regularize regional
gravity field solutions using SRBF.
5.4.1 Truncated singular value decomposition
The least-squares solution x̂ using SVD is given by (5.25) which takes all singular values of N into account.
Since very small singular values cause instability in the solution, it is common to filter the singular values to
obtain a stable or regular solution. This filtering can be performed using filter factors fk2 :
x̂ =
K
X
fk2
k=1
vkT y
vk .
s2k
(5.27)
The idea of truncated SVD is to discard some singular values to obtain a regularized solution. Hence, the filter
factor for TSVD solution reads:
(
1 for k ≤ k 0
fk2 =
0 for k > k 0
(5.28)
or equivalently using:
0
x̂tsvd =
k
X
vT y
k
k=1
s2k
vk .
(5.29)
This equation states that the truncated SVD solution is obtained from the first k 0 singular values and the rest are
ignored. Due to the lack of enough theoretical foundation, k 0 is usually chosen arbitrarily. The first obvious way
is to find k 0 such that the solution Ax̂tsvd fits well to the observations l (Scales, 1996). Some authors proposed
to use statistical criteria to define a significance level for small singular values to be discarded. See for instance
Lawless and Wang (1976) and Dempster et al. (1977). This method can also be considered as selective singular
value decomposition or in brief SSVD. The solution for SSVD reads:
x̂ssvd =
X
|vkT y|≥τ
vkT y
vk
s2k
(5.30)
where τ determines the significance of Fourier coefficients |vkT y|. Thus the SSVD method is dependent on the
choice of τ . See also Hansen (2010), Xu (1998) and Rust (1998) for more details on SSVD. As another variant
for TSVD solution, Xu (1998) proposed a quality-based TSVD method by minimizing the mean squared error.
The mean squared error of TSDV is defined as the sum of estimated error of x̂tsvd and the bias caused by
truncation.
The TSVD method is an attractive method in the sense that it eases the computation of a regularized solution
once the SVD components are computed. The only shortage of SVD technique could be its high computational
66
burden for large scale problems. However, due to the capability of current computers this issue is not a great
concern as before. Moreover, there are some mathematical techniques for the decomposition of large matrices
which reduces the computational costs. See for example Martinsson et al. (2006) and Martinsson et al. (2010)
for the randomized decomposition of matrices. For regional gravity field solutions based on satellite data, this
problem becomes even less important since the size of normal matrices on regional scales are significantly
reduced. For instance, with Nmax = 300, the size of the normal matrix will be about 6000 × 6000 for a region
as big as Central Africa (c.f. table 6.8).
An alternative to the TSVD, i.e. truncating the singular values, is to weight them properly. In other words, the
truncation can be replaced by smoothing the singular values. This can be done by either SVD techniques or
direct regularization of ill-posed problems. Direct regularization methods can improve the condition of ill-posed
normal matrices without the need for performing SVD analysis. Nevertheless, this class of regularizations can
be still described by SVD analysis with the advantage of proper weighting of SVD instead of truncation.
5.4.2 Tikhonov regularization
The most well-known direct regularization of ill-posed problems is the Tikhonov regularization which is
perhaps the most successful regularization method so far (Hansen, 2010). The key idea of regularization,
in general, is to assume a priori condition about the size and smoothness of the solution. This assumption can
be described by adding an additional model to the main equation system. To describe this, we consider the
equation (5.2) once more and this time together with its stochastic components:
Ax = l + e with Cl = σ02 P−1
l
(5.31)
therein Cl is the covariance matrix of observations. Pl and σ02 are the weight matrix and its corresponding
unknown variance factor. Even though the design matrix A is ill-posed, the least-squares assumption minimizes
the norm of residuals kAx̂ − lk. However, the solution x̂ will be unreliable according to instability of the
inversion. Therefore a trusted solution needs additional information about the unknowns. Now we suppose that
this information is given by a refining model:
2 −1
Lx = µ with Cµ = σµ
Pµ
(5.32)
in which, L describes the refining model which is known as the regularization matrix. µ is a functional
of unknown parameters x, which can also be regarded as the pseudo observation vector containing prior
2 and P are variance factor and the weight matrix of the pseudo
knowledge about the unknown parameters. σµ
µ
observations µ. Equation (5.32), together with observation equation (5.31) yields:
l
A
.
x=
µ
L
(5.33)
−2 T
−2 T
(σ0−2 AT Pl A + σµ
L Pµ L)x = σ0−2 AT Pl l + σµ
L Pµ µ
(5.34)
(N + R)x = y + u
(5.35)
The normal equation system for (5.33) reads:
or in brief:
−2 LT P L and u = σ −2 LT P µ. Introducing the regularization parameter:
where R = σµ
µ
µ
µ
γ2 =
Equation (5.34) can be reformulated as:
σ02
.
2
σµ
(5.36)
67
(AT Pl A + γ 2 LT Pµ L)x = AT Pl l + γ 2 LT Pµ µ
(5.37)
which is equivalent to the minimization process:
min{kAx − lk2Pl + γ 2 kLx − µk2Pµ }.
(5.38)
Relations (5.33) and (5.38) give the general form of regularization process for ill-posed problems. According to
this equation, the regularization components L, γ 2 and µ along with its weight matrix Pµ have to be predefined
in a proper way. Therefore, depending on how these components are determined and applied to equation
(5.37), there are several regularization methods. Among these methods, Tikhonov regularization (Tikhonov
and Arsenin, 1977) is, perhaps, the most well-known method for ill-posed problems. The key idea of Tikhonov
regularization is to find a solution with a priori assumption about the covariance matrix of unknown parameters
which is given by R. If µ = 0 and Pµ = I in equation (5.37), the Tikhonov regularization will be:
(AT Pl A + γ 2 LT L)x = AT Pl l
(5.39)
in which L has to be defined depending on the particular application and γ 2 should be chosen carefully. L is a
linear operator with certain smoothness constraints. The influence of L is addressed in details in Hansen (1997).
Ilk (1993) showed that Tikhonov regularization for gravity field modelling based on satellite data is insensitive
to the choice of L and it can be well approximated by a unit matrix. Setting L = I means the prior information
is available for the unknown vector x and not for its functional such as first or second derivatives. This also
guarantees the existence of a solution x̂ which is close to its exact value x̂ex , so that kx̂ − x̂ex k is minimized
(MacLeod, 1988). In this case the Tikhonov regularization is called standard Tikhonov regularization and is
also known as ridge regression in statistics. In this PhD thesis we also set L = I and confine ourselves to the
proper choice of the regulariuation parameter γ 2 . In this case, the (standard) Tikhonov regularization (5.39)
reads:1
(AT Pl A + γ 2 I)x = AT Pl l
(5.40)
min{kAx − lk2Pl + γ 2 kxk2I }.
(5.41)
with the minimization procedure:
The Tikhonov-regularized solution, x̂γ , will be obtained using:
x̂γ = (AT Pl A + γ 2 I)−1 AT Pl l.
(5.42)
According to (5.41), not only the norm of residuals kAx − lk will be minimized, but also the solution norm
kxk is enforced to be minimum which implies a smoothness or regularity for the solution. Without a proper
regularization, the estimated coefficients x̂ can be physically meaningless tough they satisfy the condition min
kAx̂ − lk2Pl . Figure 5.5 illustrates this clearly. The estimated coefficients for regional gravity field solution
based on simulated GRACE data (see section 6.2.2) are shown in this figure. The first plot on the top, shows
the estimated coefficients without any regularization and the second plot displays the estimated coefficients by
means of a proper regularization method.
1
It should be mentioned that even if L 6= I, it is still possible to transform the problem to the standard case. To do so, it is enough to
multiply both sides of (5.39) by R−1 so that the corresponding normal equations reads:
(N̂ + γ 2 I)x = ŷ
in which, N̂ = R−1 N and ŷ = R−1 y. Hence the discussions concerning the standard Tikhonov regularization, can be generalized
to the case with L 6= I.
68
Figure 5.5: The estimated coefficients for the regional gravity field solution in section 6.2.2. top: No
regularization is applied and the solution is simply obtained based on least-squares method. bottom:
the solution using a proper regularization method. The non-regularized solution is undesirably
oscillatory. The values of these coefficients are about 6 orders of magnitude larger then the
regularized solution. Note that these two figures have different vertical scales.
The norm of residuals i.e. kAx̂ − lk is almost the same for both sets of coefficients. In contrast, the norm of
the non-regularized solution i.e. kx̂k, is about 6 orders of magnitude larger than the norm of the regularized
solution. As it can be seen in the figure 5.5, the standard least-squares solution contains undesirably large
oscillations especially in the tails of the unknown vector. This makes the solution to be a physically meaningless
estimation even though it mathematically satisfies Ax̂ = l̂. Therefore the condition (5.41) will also control
the smoothness of the solution based on the given weight or regularization parameter γ 2 . The choice of the
regularization parameter is a trade-off between the norm of the residuals and the smoothness of the estimated
coefficients. Too large γ 2 values lead to over-smoothing of the solution i.e. to loose some information contained
in the observation. On the other hand, choosing too small regularization parameter results in a physically
meaningless solution.
The regularization parameter should be usually chosen from a set of numbers which span several orders of
magnitude. This implies a high computational burden to find the right number if it is done empirically. Using
SVD in the regularization process, gives an insight into the approximate value of regularization parameter and
helps to find the proper parameter very fast.
5.4.3 Tikhonov regularization in terms of SVD
As we explained before, it is possible to describe the Tikhonov regularization in terms of singular value
decomposition. To do this, we can rewrite (5.40) as:
(N + γ 2 I) x = AT Pl l.
| {z }
Ñ
The regularized normal matrix Ñ can be decomposed using SVD:
(5.43)
69
Ñ = N + γ 2 I = VS2 VT + γ 2 I.
(5.44)
Since V is an orthonormal matrix with VVT = I, we can write:
Ñ = VS2 VT + γ 2 VVT
(5.45)
Ñ = V(S2 + γ 2 I)VT = VS̃VT .
(5.46)
or simply:
We consider S̃ as the regularized matrix of singular values. Equation (5.46) indicates that only the singular
values of the normal matrix N (or equivalently its eigenvalues) will be different as a result of standard Tikhonov
regularization.
Using (5.46) and (5.43), the Tikhonov-regularized solution (5.42) can be obtained in terms of singular value
decomposition of N and the regularization parameter γ 2 :
x̂γ = Ñ−1 y = VS̃−1 VT y.
(5.47)
Furthermore the singular values of Ñ will be:
s̃2k = s2k + γ 2
(5.48)
therefore analogous to (5.25) one can obtain:
x̂γ =
K
X
vT y
k
k=1
s̃2k
vk
(5.49)
or equivalently using (5.27), in terms of filter factors fk2 defined by:
fk2 =
s2k
.
s2k + γ 2
(5.50)
See also Hansen (1997) and Hansen (2010) for more details. The filter factors fk2 determine the contribution
of the singular values to the solution. Therefore the Tikhonov regularization can be considered as the weighted
or filtered SVD solution or WSVD. From signal processing view, fk2 can also be interpreted as the coefficients
of a low-pass filter. The difference between truncated SVD and Tikhonov regularization (or WSVD) lies in the
difference between their corresponding filter factors. Comparing the filter factors for truncated SVD given by
(5.28) and filter factors for the Tikhonov regularization in (5.50), demonstrates that TSVD is an exact low-pass
filter while Tikhonov regularization is a smooth one. Figure 5.6 shows the TSVD and Tikhonov filter factors
for the ill-posed singular values shown in figure 5.4 (right). For TSVD the truncation point is assumed to be at
850th singular value i.e. k 0 = 850 in (5.28).
70
(a)
(b)
Figure 5.6: (a): the filter factors for truncated SVD (red) as well as Tikhonov regularization (black). The
former is an exact low-pass filter while the latter exhibits a smooth low-pass filter. (b): singular
values of an ill-posed problem (black), truncated singular values at k 0 = 850 (red) and the
Tikhonov regularized singular values (blue). The intersection of horizontal and vertical lines has
the coordinate (850, s2850 ). k 0 = 850 shows where truncated singular values end and s2850 is the
regularization parameter for Tikhonov regularization and is the number to which the regularized
singular values (blue) settle down.
The corresponding Tikhonov filter factors for the assumption k 0 = 850 can be obtained if γ 2 = s2850 so that
2
the value of 850th filter factor reaches half of its maximum i.e. f850
= 0.5. Figure 5.6 also illustrates the
corresponding truncated singular values as well as the Tikhonov regularized singular values. Evidently the
value to which the Tikhonov-regularized singular values settle down, is the chosen regularization parameter.
This number is also where the truncated singular values end. This is shown by the intersection of the vertical
and horizontal line in figure 5.6.
From figure 5.6 it also follows that a mathematically meaningful regularization parameter lies between the
smallest and the largest singular values of N. If γ 2 is chosen less than the smallest singular value, it does
have no effect on the solution. Respectively if a γ 2 bigger than the largest singular value is to be used, the
linear operator N looses its effect on the solution. This leads to the following proposition for the bounds of the
regularization parameter:
Proposition: In the standard Tikhonov regularization, the regularization parameter γ 2 is bounded by the
smallest and the largest singular values of the associated normal matrix, i.e.
s2K < γ 2 < s21 or similarly kN−1 k < γ 2 < kNk.
(5.51)
Although the bounds of γ 2 in this relation gives a theoretical insight into the value of regularization parameter,
it, numerically, introduces a very large domain for the regularization parameter. According to figure 5.4 (b) the
singular values (for this specific problem) span 20 orders of magnitude and the regularization parameter will be
a number between 106 and 1026 with a condition number about 1021 .
Therefore the selection criteria for γ 2 is the main and the most critical task in all regularization methods. In the
following some well-known methods will be considered in detail.
To end this section and similar to equation (3.40), for global gravity field modelling, it is also necessary
to estimate the covariance matrix of estimated parameters for regional solutions from (5.42) or (5.47). The
regularized covariance matrix C̃x̂ can be obtained by applying the covariance law to (5.42):
C̃x̂ = (
∂x̂ −1 ∂x̂ T
T
2 −1
)P ( ) = (AT Pl A + γ 2 I)−1 AT Pl P−1
l Pl A(A Pl A + γ I)
∂l l ∂l
(5.52)
5.5 The choice of the regularization parameter
71
or briefly:
C̃x̂ = Ñ−1 NÑ−1
(5.53)
which gives the formal covariance matrix for the estimated coefficients. The calibrated covariance matrix will
be computed using the a posteriori variance factor given by (3.41).
(5.53) can also be rewritten by means of singular value decomposition of N and Ñ:
C̃x̂ = VS̃−2 VT VS2 VT VS̃−2 VT
(5.54)
C̃x̂ = VS̃−2 S2 S̃−2 VT
(5.55)
and since VT V = I:
which shows the impact of the regularization on the variance and covariances of the estimated parameters.
The regularization parameter γ 2 is the most important regularization component and plays a significant role in
regularization. It sets a balance between the contribution of the normal matrix N and the prior information R
to the solution x̂γ . If γ 2 = 0 it implies that the reliable solution can be obtained without any regularization
and thus x̂γ = x̂. A larger γ 2 means more ill-posedness and consequently more prior information needed for
the solution. This trade-off between the norm of the solution and the norm of residuals, makes the choice of
regularization parameter a sensitive task. In practice, there are several criteria used to select a proper γ 2 , each of
them may suite better for some specific problems. Discrepancy principle, Normalized cumulative periodogram
(NCP analysis), L-curve criterion, Generalized cross validation and variance component estimation are some
known methods for the choice of regularization parameter. The first two methods are given in Hansen (1997,
2010) and will not be considered here. The rest will be given in the following with more details. Furthermore,
we introduce our proposed criterion for the choice of γ 2 which suits better for the regional gravity field
modelling using SRBF. In chapter 6, we use these methods for regional gravity field modelling based on satellite
data.
5.5.1 Generalized cross validation
The idea of Generalized Cross Validation (GCV) is to minimize the norm of residuals using the leave-out-one
approach. This is a well-known method in geodetic literature for statistical tests. According to Golub et al.
(1979), a good regularization parameter γ 2 is a minimizer of the function G(γ 2 ) defined by:
G(γ 2 ) =
IkAx̂γ − lk2
[trace(I − Qγ 2 )]2
(5.56)
where I is the number of observations and Qγ 2 is the so-called influence matrix and is defined by:
Qγ 2 = AÑ−1 AT
(5.57)
where N̂ is the regularized normal matrix as given in (5.44). Therefore the chosen regularization parameter
should minimize the function G(γ 2 ). A key difficulty concerning (5.56) is the calculation of the trace in the
denominator. The size of influence matrix is I × I and for large scale problems, computations of trace is rather
expensive. Hutchinson (1990) proposed a statistical trace estimator to overcome this problem. Another way to
72
ease the calculation of the trace is to use the SVD of the normal matrix. For this purpose, we can rewrite the
denominator as follows:
trace(I − Qγ 2 ) = trace(I) − trace(Qγ 2 ) = I − trace(Qγ 2 )
(5.58)
since trace(pq) = trace(qp) one can assume p = AÑ−1 and q = AT which yields:
trace(Qγ 2 ) = trace(AÑ−1 AT ) = trace(AT AÑ−1 ) = trace(NÑ−1 )
(5.59)
and taking SVD of N and N−1 :
trace(NÑ−1 ) = trace(VS2 VT VS̃−2 VT ) = trace(VS2 S̃−2 VT )
(5.60)
and finally:
2 −2
trace(Qγ 2 ) = trace(VS S̃
T
V )=
K
X
k=1
s2k
s2k + γ 2
(5.61)
Therefore (5.56) can be written as:
G(γ 2 ) =
IkAx̂γ − lk2
.
K
P
s2k
(I −
)2
2
2
k=1 sk + γ
(5.62)
This equation gives a convenient way of computing the GCV function in terms of the regularized singular
values. See also Chung et al. (2008) and Save (2009).
The generalized cross validation function G given by (5.56) or (5.62) is related to the a posteriori variance
factor for the covariance matrix of observation as given by (3.41). It has been used in geodetic literature for
the calibration of covariance matrices as well as in the statistical tests after least-squares adjustment. See, e.g.
Vanicek and Krakiwsky (1982) or Koch (1999). The difference is that the denominator which is the degree of
freedom, df , is a function of the regularization parameter and is not constant. Therefore the generalized cross
validation can be seen as a method to minimize the a posteriori variance factor σ̂02 , using a proper regularization
method.
Figure 5.7: The generalized cross validation function for the choice of regularization parameter
Figure 5.7 displays the GCV function associated with the regional gravity field solution described in section
6.2.2, for a set of regularization parameters. The point where G is minimum is marked in this figure. The
73
generalized cross validation has been used in many research studies. Alberts (2009), Bouman (2000), Lio
(2008), van Loon (2008) and Xu (2009) used GCV for the choice of regularization parameters in their analyses.
GCV can be used for other optimization issues as well. See for instance Tenzer and Klees (2008) where they
used GCV to choose an optimal depth of SRBF.
A remarkable benefit of GCV is that it works based on the residuals’ norm and is a data-dependent method.
This is especially desired for global gravity field modelling where data are globally available. For regional
gravity field determination based on satellite data the criterion may not suit well. Because even though the
observations at satellite altitude are well represented using the solution (so that the GCV function is minimized),
a satisfactory representation on the Earth’s surface is not necessarily guaranteed due to additional ill-posedness
caused by the downward continuation. This issue will be discussed more in chapter 6 where the GCV will be
used for the regularization of regional gravity field solutions based on satellite data.
5.5.2 Variance component estimation
The method of variance (and covariance) component estimation or VCE is the estimation of an unknown
variance factor for the known symmetric positive-definite covariance matrix of observations. It is a useful
method when several data sets have to be combined in a parameter estimation procedure. See e.g. Koch (1999)
and Amiri-Simkooei (2007).
One can consider the pseudo observations µ given in the refining model (5.32) as an additional data set to
be combined with the observations l in model (5.31). According to equations (5.31) and (5.32), two variance
2 are unknown and shall be estimated using variance component estimation. Therefore
components σ02 and σµ
the variance component estimation can be used for choosing γ 2 in Tikhonov regularization since it is the ratio
2 as given by (5.36). The variance components σ 2 and σ 2 can be estimated using:
of σ02 and σµ
µ
0
(
σ02 = (êT Pl ê)/dfl , ê = Ax̂γ − l
2 = (δx̂T P δx̂)/df , δx̂ = Lx̂ − µ
σµ
µ
µ
γ
.
(5.63)
Since in standard Tikhonov regularization (5.40), L = Pµ = I, µ = 0 and furthermore we assumed that
Pl = I, equations (5.63) can be rewritten as:
(
σ02 = (êT ê)/dfl
2 = (x̂T x̂ /df
σµ
µ
γ γ
.
(5.64)
The partial redundancies dfl and dfµ can also be obtained by (Koch and Kusche, 2002):

1


dfl = I − 2 trace(NÑ−1 )
σ0
1

dfµ = K − 2 trace(Ñ−1 )

σµ
.
(5.65)
Using SVD of N and Ñ and according to (5.61), the redundancy numbers can be evaluated using singular
values s2k :

K
s2k
1 P


dfl = I − 2
2
σ0 k=1 sk + γ 2
K
1 P


dfµ = K − 2
(s2 + γ 2 )
σµ k=1 k
.
(5.66)
Due to the fact, that the variance components and the redundancy numbers are dependent, the variance component
2 is necessary.
estimation is an iterative process where a first initial guess for σ02 and σµ
74
Variance component estimation has been shown to be a successful method of data combination and regularization
in many applications. There are several examples in the context of gravity field modelling where VCE has been
used as a method for regularization and weight estimation. Kusche (2003) used the VCE method for the optimal
weight determination in gravity field recovery based on GOCE data. Kusche and van Loon (2005), van Loon
and Kusche (2005) employed the VCE to assess the stochastic model of CHAMP data using the energy balance
approach. For a rather complete list of research studies, where VCE is used for analysing geodetic data such as
GPS data processing or gravity field modelling, see Amiri-Simkooei (2007).
5.5.3 L-curve analysis
The L-curve analysis is a graphical tool for regularization of discrete ill-posed problems. The idea was proposed
by Hansen (1990b) and Hansen and OLeary (1993) and soon attracted very much attention in the solution of
discrete ill-posed problems.
The L-curve is a logarithmic plot of the residuals’ norm, kAx̂γ − lk versus the solution norm kx̂γ k. This curve
is obtained based on a set of regularization parameters γ 2 , and their corresponding solutions x̂γ . The parametric
equation of the L-curve is:
(
xL = log kAx̂γ − lk
yL = log kx̂γ k
.
(5.67)
Figure 5.8 (a) illustrates a typical L-curve plot. The idea of using this curve, for the choice of regularization
parameter, is directly connected to minimum norm condition given by (5.41).
(a)
(b)
Figure 5.8: (a): the L-curve function and its corner point where the norm of the solution and the norm of
residuals compromise a minimum. (b): the curvature of the L-curve. The maximum curvature
refers to the corner point of the L-curve.
As it can be seen from figure 5.8 (a), the name ’L-curve’ refers to the fact, that this curve visually appears like
an ’L’ shape with a vertical and horizontal part. The corner point of the ’L’ shape is the point where the norm of
residuals and the solution norm compromise their minima. To find the regularization parameter corresponding
to the corner point of the L-curve, (Hansen, 1997) suggested to find the point on the L-curve which has the
maximum curvature. To do this, one can fit a function to the L-curve which is at least two times differentiable.
Thus the curvature of L-curve can be calculated as follows:
x0 y 00 − yL0 x00L
.
k(xL , yL ) = qL L
02 )3
(x02
+
y
L
L
(5.68)
75
The maximum value of k(xL , yL ) corresponds to the corner point and is, consequently, assigned to the desired
regularization parameter. Figure 5.8 (b) shows the curvature of the L-curve in 5.8 (a).
Xu (1998) proposed another way to find the corner of the L-curve. Since the corner point is the closest point of
L-curve to the origin, it is enough to minimize the distance of the L-curve coordinates (xL , yL ) from origin.
Reginska (1996) tried to describe the mathematical features of the L-curve. She gave a theoretical justification
for choosing regularization parameter assigned to the corner point. Later Hansen (2000) extended Reginska’s
work into more details. Clavetti and co-authors investigated the L-curve and its curvature for Tikhonov
regularization in a series of papers. They estimated the L-curve and the bounds of its curvature using Lanczos
bidiagonalization. See more details in Calvetti et al. (1999), Calvetti et al. (2002) and Calvetti et al. (2004).
The L-curve analysis has been used in numerous research studies for variety of different applications. It has also
been used for ill-posed problems in gravity field determination. In a simulation study Kusche and Klees (2002)
compared the performance of the L-curve analysis to generalized cross validation for Tikhonov regularization
of gravity field modelling based on SGG data. They concluded that L-curve yields over-smooth solutions in
their analyses and suggested to use L-curve with cares. In contrast, Save (2009) used the L-curve criterion for
regularization of global solutions using real GRACE data to reduce errors in monthly GRACE solutions and
reported the success of the method. Later, Save and Bettadpur (2012) showed that use of L-curve and applying
Lanczos bidiagonalization results in remarkably reduced stripe errors compared to CSR GRACE unconstrained
solutions RL04. The L-curve method has been also used by Ramillien et al. (2011) for the inversion of surface
water mass anomalies from GRACE data. They computed the maximum curvature of the L-curve using (5.68)
and used the benefits of fast computations using SVD-based Tikhonov regularization.
5.6 Signal-adaptive parameter choice: The parameter-signal
correlation (PSC)
In section 3.3, it was shown that the estimated scaling coefficients αk resemble the shape of the gravitational
potential or geoid, see figure 3.7. The cross correlation function for the estimated coefficients and geoid heights
at the same locations were also computed which shows a high correlation between the estimated coefficients
and the signal to be modelled using SRBF (figure 3.7). The reason is the space-localizing property of SRBF;
the energy of a SRBF is concentrated around its centre and consequently the corresponding coefficients are
significantly determined by observations around it. This fact can be seen if we consider the general form of the
gravity field synthesis using SRBF as (see also 3.3)
V (ri ) =
K
X
αk B(rk , ri )
(5.69)
V (ri ) =< x, B(rk , ri ) >
(5.70)
k=1
which can be written in terms of the inner product
where x = [α1 , α2 , ..., αk ]T is the vector of unknown coefficients. These relations can be approximately
expressed by means of the convolution of the functions αk and B(rk , ri ):
V (ri ) = x ∗ B(rk , ri ).
(5.71)
The SRBF defined by (3.50) have two properties which can be used for the regularization purposes. Firstly,
B(rk , ri ) is a (spherically) symmetric function. This implies that the convolution given by (5.71) can be
equivalently expressed by the cross-correlation function 1 . Therefore the synthesized values Vi are nothing
1
According to the definition of the convolution and the cross-correlation, if the kernel function g(τ ) is symmetric i.e. g(τ ) = g(−τ ),
the convolution and the cross correlation of g with any other function are equivalent. See e.g. Yarlagadda (2010) and Steven (1997).
76
but the cross correlation of αk and the symmetric base function B at different positions. Secondly, the base
functions B have their maximum value at their centre, i.e. at ri = rk . In other words, B does have the
space-localization feature as explained in the previous chapters. If B were an ideal space-localizing function
i.e. the Dirac function, Vi and αk would be identical. Nevertheless, the coefficients αk should correspond to
the synthesized values Vi around the position rk since the base functions B are space-localizing.
These features can be considered as prior knowledge about the unknown coefficients and one can make use of
this for the regularization purposes. The idea of the signal-adaptive parameter choice is, therefore, based on this
property: A good regularization parameter provides a solution where the estimated scaling coefficients
have maximum correlation with the (residual) gravitational potential.
The mathematical description of this method can be expressed as follows:
Let the scaling coefficients at locations φk and λk be denoted by αk (γ 2 , φk , λk ) where γ 2 is the corresponding
regularization parameter. Furthermore the function dV 1 , which is to be modelled using SRBF, is available at
grid points φk and λk . The desired regularization parameter γ 2 is chosen such that the scaling coefficients αk
and the signal dV have the maximum correlation. In other words, αk and dV should be as (much) similar as
possible. To measure the similarity, one can use the normalized cross correlation function Γxy (τ ) defined by
E[x(t)y(t + τ )]
Γxy (τ ) = p
E[x(t)]E[y(t)]
(5.72)
where E is the expectation operator and x and y are two arbitrary functions. τ defines the lag of the cross
correlation function (Orfanidis, 1996). Since we are interested in the correlation of dVk and αk at the same
positions, the cross correlation function is needed only at zero lag, i.e. τ = 0:
E[x(t)y(t)]
Γxy (0) = p
E[x(t)]E[y(t)]
(5.73)
which can be equivalently expressed by the inner product:
Γxy (0) =<
y
x
,
>.
kxk kyk
(5.74)
Therefore the similarity between dVk and αk can be measured using
ΓdVk ,αk (0) =<
dV
αk
,
>.
kdV k kαk k
(5.75)
The correlation function ΓdVk ,αk (0) determines the linear dependency between αk and dVk which is expected
to be significantly high. Thus using (5.75), the regularization parameter γ 2 can be obtained by the following
criterion:
The desired regularization parameter γ 2 is the maximizer of the function ΓdVk ,αk (0) given by (5.75).
We call this parameter choice method as the parameter-signal correlation or briefly the PSC method.
Figure 5.9 shows the function ΓdVk ,αk (0), associated with a set of regularization parameters used to determine
the regional gravity field in Central Africa based on the simulated GRACE data (see 6.2.2). As it can be seen,
the function does have a maximum which corresponds to the desired regularization parameter.
The key point of using (5.75) is to obtain a priori value for dV at grid locations φk and λk . It can be
computed using either regional gravity field models (if available) or existing global models. This implies
1
dV refers to the residual potential since for regional gravity field modelling the long wavelengths should be removed.
77
Figure 5.9: The PSC function for a set of regularization parameters. The maximum correlation is assigned
to the desired regularization parameter. In this figure the 187th selected parameter is the desired
regularization parameter.
that a high-resolution gravity field model should be available to obtain dVk . According to (5.75), it is necessary
to evaluate the residual potential dV on grid locations φk and λk using:
dV (φk , λk ) = V (φk , λk ) − V0 (φk , λk )
(5.76)
where V (φk , λk ) is the gravitational potential and V0 (φk , λk ) refers to the long wavelengths of the potential
field which should be removed. V0 is computed and subtracted according to discussions given in 4.2.3. To
assess the effect of using different models to obtain dVk , we used several geopotential models listed in table
5.1 for the regional gravity field model in Section 6.3.3. Our computation indicate that by using different
reference models to compute dVk , the maximum value of the function ΓdVk ,αk (0) does not change significantly.
Consequently the resulting regularization parameter does not change remarkably as shown in table 5.1. It can
be seen that if the geopotential models EGM2008 and EGM1996 are employed to compute dVk , the resulting
regularization parameters will be 1.65 × 1024 and 1.89 × 1024 , respectively. The difference between these
values is rather small especially if we compare it with the regularization parameters obtained using the VCE,
GCV or L-curve (see table 6.9). Using these two regularization parameters we estimated two sets of scaling
coefficients, and then the geoid heights in this region were synthesized. Figure 5.10 shows the regional geoid
differences between two models obtained using the above regularization parameters. As it can be seen, the total
regional RMS is about 1.1 cm with the maximum value of about 6 cm in a few specific locations. Again, such
deviations are not remarkable if they are compared to the results obtained using other methods of regularization
(see Figure 6.18). Nevertheless one can try to refine the results to still eliminate the residuals by modifying the
PSC method and reducing the impact of the reference geopotential model. Overall, we concluded that almost
all models provide rather the same regularization parameter at the current accuracy level for satellite-derived
gravity fields. Therefore there is no preference given to a specific geopotential model for the PSC approach.
This means that the prior model used for the PSC method does not have to be the state-of-the-art. Only an
approximate model which can show the geometry of the field, fulfils the purpose of the PSC method.
Using (5.75) to find the regularization parameter gives an insight into easy and straightforward computations.
It provides satisfactory and even better results compared to other parameter choice methods such as L-curve or
variance component estimation. In chapter 6, we will use this method and compare it to other parameter choice
methods introduced in this chapter.
78
data used
Nmax
year
resulting γ 2
GOCO03s
GRACE, GOCE
250
2011
1.31 × 1024
GGM03c
GRACE, Terrestrial
360
2009
1.48 × 1024
EGM2008
GRACE, Altimetry, Terrestrial
2190
2008
1.65 × 1024
PGM2000
Altimetry, TOPEX,ERS1, Terrestrial
360
2000
1.90 × 1024
Reference model
EGM1996
Altimetry, TOPEX,ERS1, Terrestrial
360
1996 1.89 × 1024
Table 5.1: Different geopotential models used to compute dVk for the PSC method. The second column shows
the data used to determine the gravity field model. See GFZ (2013) for more details about these
models. The resulting regularization parameter is also shown in the table for the regional gravity
field model in Section 6.3.3. As it can be seen, all models give approximately the same regularization
parameter.
Figure 5.10: Geoid differences between two regional models obtained using the PSC regularization method but
with different reference geopotential models; the EGM2008 and the EGM1996. The total geoid
RMS is about 1 cm with maximum deviation of about 6 cm. See Section 6.3.3. for more details
about regional solution in this region.
5.7 Initial value for the regularization parameter
A good first guess for the regularization parameter is necessary for all parameter choice methods. Existence of
such an approximate value reduces the computational costs and leads to a faster convergence. Once the initial
guess for the regularization parameter is obtained, it can be improved by means of iteration in the variance
component estimation or criteria such as the L-curve analysis, the generalized cross validation or the the PSC
method. The final regularization parameter is expected to be close to the initial guess. Therefore it is possible
to define a search band for the regularization parameter in the neighbourhood of the initial guess as shown in
figure 5.11. Our computations indicate, that this approach considerably helps to decrease computational costs
and provides a rapid convergence in the iterations.
In this section, we propose two different ways to obtain a first realistic guess for the regularization parameter.
The basic tool for these two methods are the singular values of the normal matrix. In addition, in both cases we
5.7 Initial value for the regularization parameter
79
benefit from the fact that the spherical harmonics and SRBF span the same function space on the global scale.
Figure 5.6 (b) shows the singular values of an ill-posed normal matrix. In addition, the Tikhonov-regularized
Figure 5.11: The regularized singular values (black) using initial guess for the regularization parameter and the
original non-regularized singular values (red). The regularized singular values are now stable and
level out at value γ 2 = 1023 . The search band displays the area where the final regularization
parameter is located.
singular values as well as truncated singular values are also shown. As we discussed in the context of this figure,
the number to which the Tikhonov-regularized singular values level off, is the truncation point for truncated
singular values. This point has the coordinates (n, s2n ). The horizontal component or n, gives an insight into
the number of significant singular values, needed to obtain a good solution. On the other hand, the vertical
component or s2n refers to the amount of regularization needed for the solution. A good initial guess can be
found if either n or s2n are approximately known. Therefore, we propose two ways to find an initial first guess
for the regularization parameter:
• using information about n which is based on the size of the region
• using information about s2n which is based on the ’desired’ condition number
In the following we discuss these two methods.
5.7.1 Initial guess based on the size of the region
Figure 5.4 (a) displays the singular values related to global gravity field modelling using SH as well as SRBF
up to max degree Nmax = 70 (i.e. the number of SH functions are 5038). The sudden jump in singular values
related to SRBF at n = 5038 explicitly shows that only the first 5038 singular values are necessary to obtain
an equivalent solution to SH. This is due to the fact that spherical harmonics and SRBF span the same function
space on the global scale (see section 3.3).
One can use this equivalence between SH and SRBF to (approximately) find the number of significant singular
values for regional solutions. Since the number of significant singular values on the global scale is (Nmax +
1)2 , the number of significant singular values on regional scales can be approximately estimated by a simple
proportion based on the area of the region using
k0 =
AΩ
(Nmax + 1)2
4π
(5.77)
80
where AΩ denotes the size of the region on the unit sphere and is given by:
Z
λ2
Z
φ2
cosφdφdλ = (λ2 − λ1 )(sin φ2 − sin φ1 ).
AΩ =
λ1
(5.78)
φ1
The boundaries of the region are defined by λ1 , λ2 , φ1 and φ2 . Therefore, the initial guess for the regularization
parameter is equal to the k 0th singular value of the associated normal matrix. For instance if the regional
gravity field is desired in the region defined by λ1 = 0, λ2 = 50, φ1 = 50 and φ2 = 75, using SRBF with
Nmax = 250, the number of significant singular values is approximately equal to 870. Thus, the initial guess
for the regularization parameter is the 870th singular value i.e. s2870 .
5.7.2 Initial guess based on the condition number
Another method to obtain a realistic initial value for the regularization parameter is to use the condition number.
To do this, we consider the condition number of the normal matrix given by
cond(N) =
s21
kNk
= 2
s2K
sK
(5.79)
in which s21 and s2K are the first and last singular values of N (see also 5.23). The same holds for the regularized
normal matrix Ñ:
kÑk
s̃21
= 2 .
2
s̃K
s̃K
(5.80)
(
s̃21 = s21 + γ 2 = kNk + γ 2
s̃2K = s2K + γ 2 .
(5.81)
cond(Ñ) =
From (5.48) it follows that
Therefore (5.80) becomes
cond(Ñ) =
s̃21
kNk + γ 2
=
.
s̃2K
s2K + γ 2
(5.82)
Due to the fact that kNk γ 2 and γ 2 s2K , (5.82) can be well approximated by
kNk
cond(Ñ) ∼
= 2
γ
(5.83)
which results in a rather explicit relation for the regularization parameter:
γ2 ∼
=
kNk
cond(Ñ)
.
(5.84)
This means that if prior information about the condition number of the ’desired’ regularized normal matrix Ñ
is available, the regularization parameter γ 2 can be determined directly.
According to the discussions concerning equations (4.2) and (4.3), the ill-posed regional normal matrix N is in
fact extracted from the global normal matrix Nsrbf . The strong ill-posedness of N is due to the horizontal and
vertical truncation of Nsrbf (see 4.1). Therefore, by means of regularization, we try to repair these ’cutting’
effects such that the regularized normal matrix Ñ be as stable as Nsrbf .
Based on this argument, we postulate the following assumption to obtain an initial value for γ 2
cond(Ñ) = cond(Nsrbf )
(5.85)
5.8 Different types of SRBF and their impact on the regularization
81
where Nsrbf is the normal matrix associated with the global gravity field modelling using SRBF. Since SRBF
and SH span the same space function
cond(Nsrbf ) = cond(NSH )
(5.86)
and the condition number of NSH can be approximately estimated using Kaula’s rule of thumb (Kaula, 1966,
Knudsen, 1987)
cond(NSH ) =
3
Nmax
8
(5.87)
where Nmax is the maximum degree of expansion. Putting (5.85), (5.86) and (5.87) together, the initial value
for γ 2 can be obtained from
γ2 =
8kNk
3
Nmax
(5.88)
which evaluates the initial regularization parameter using the norm of the normal matrix and the maximum
degree of expansion. In the following chapter, we use these two approaches to estimate an initial γ 2 . This will
also be shown that both methods give rather close initial values.
5.8 Different types of SRBF and their impact on the regularization
In section 4.2.1 we explained, that different kinds of SRBF can have different effects on the regularization
process. The reason is the smoothing properties of some SRBF defined by the Legendre coefficients bn . In this
section we discuss this issue in more detail.
In principle, the goal of regularization for regional gravity field modelling is the suppression of the model errors
(omission, commission and cut-off errors) to obtain a solution with the least possible error. If we note equation
(5.11) once more
kδxk
kek
≤ cond(A)
kxk
klk
it is evident that the solution error is dependent on the condition number of the design matrix (and the normal
matrix) as well as the observation errors. Therefore, to reduce the solution’s error one should either reduce
the condition number or the observation error or both. The aim of regularization procedure is to improve the
condition number by modifying the normal matrix N. The regularized normal matrix Ñ = N + γ 2 I, has a
condition number which is considerably smaller than the condition number of N. As the result, the solution’s
error in (5.11) will be drastically reduced. Our investigations show that the use of different SRBF does not
noticeably improve the ill-posedness of the design and normal matrices. The reason is that the rapid decay of
the singular values of the normal matrix N and its rather large condition number are mainly dependent on the
size of the region which does not remarkably change by using different SRBF.
The main difference between different types of SRBF is their impact on the vector of observations l. To explain
this, we reconsider the regularized solution (5.42) from another perspective:
x̂γ = (AT Pl A + γ 2 I)−1 AT Pl l .
| {z }
|
{z
}
Ñ
(5.89)
y
According to (5.89), the regularized solution x̂γ is obtained from the observation vector l via a sequence of
linear operations. In the first step, the observation vector l is projected from the observation space L to its dual
space L0 using the weight matrix Pl . The result is the vector Pl l in the space L0 . In this step, the observations
82
are normalized according to their variances. If only one type of observation is used, the vector Pl l is just a
scaled version of l.
Then the vector Pl l will be projected onto another function space using AT . This function space denoted by
X0 is the dual space of the unknown function space X. The result of this projection, is the vector y = AT Pl l in
the function space X0 . In this projection, the observation vector l will be filtered due to the smoothing effects
of the SRBF as the row vectors of AT .
In the last step the vector y is projected onto the function space X using the operator N−1 to obtain the final
solution. Since N−1 is an unstable operator, (N + γ 2 I)−1 shall be used to obtain the regularized solution. The
whole operation sequence is diagrammatically shown in figure 5.12.
The shape of SRBF, affects the second projection and consequently the vector y. If SRBF have no smoothing
effects, the vector y includes all frequencies of l. Otherwise, the observation vector l will be filtered in the
second step. A result of this filtering is the reduction of the observation noise and according to (5.11), the
solution’s error will be reduced. If the observation noise is reduced in the second operation, less regularization
will be needed in the inversion process (third operation). From this point of view, it may seem logical to use
some sort of SRBF which contain built-in filters. The CuP, Blackman and Spline kernels are examples of these
functions which reduce the observation’s noise before the inversion process by filtering the high frequency
components of l.
Nevertheless, applying any kind of filtering to the observation vector leads to the loss of some signal components,
particularly the higher frequencies. This is a contradiction of the main goal of regional modelling which is, to
extract more local features (high frequencies) out of the data. To avoid this problem, one should be aware of
the filtering properties of the employed SRBF.
In our methodology, we always use the SRBF with the Shannon kernel with no filtering features. Thus, the
observation vector l and its noise will remain untouched and the solution error will be minimized via a proper
regularization process in the final stage. In addition, we set the maximum degree of expansion, i.e. Nmax , to
be slightly higher than the expected value. For example, if the expected resolution of solutions based on GOCE
observations is about n = 250, we set Nmax = 300. This makes the Shannon kernel to be an exact low-pass
filter where the cut-off frequency is far beyond the expected frequency content of the signal. Therefore it is
guaranteed that the observation vector is not filtered out in the second operation.
5.9 Assessment of regional solutions
83
Figure 5.12: The sequence of matrix operations to obtain the regularized solution from the observation vector.
In the first operation, the observations are projected onto an interim function space called the dual
space of L. The second step, is the projection onto the dual space X. In this step, the observations
might be filtered out if the base functions have the smoothing property. Finally, the last projection
is the inversion process which gives the final solution. The diagrammatic view of the standard
least-squares solution (without regularization) is described by Mohammad-Karim (1981).
The choice of the Shannon kernel for the shape of the SRBF makes the choice of base functions very simple.
There is no more efforts needed to define the Legendre coefficients bn as they are all equal to 1. The use of
other SRBF for regional gravity field modelling such as Blackman and CuP is also possible provided that the
bandwidth of these functions are selected properly to avoid filtering of the signal parts. As a result, the number
of base functions increases remarkably which seems to be unnecessary. The discussions concerning the number
of base functions is given in Section 4.2.1.
5.9 Assessment of regional solutions
Having obtained the solution for the unknown vector x̂, we have to assess the quality of the estimated parameters.
In global gravity field modelling based on satellite data, there are some measures used to check the quality of
the solution. Bouman (2000) introduces several quality measures used to assess the quality of satellite-based
gravity models. These measures can be classified into three groups: statistical assessment, external validation
and model-dependent evidences.
5.9.1 Statistical assessment
This group of quality measures consists of information obtained from observations and their given covariance
matrices. The statistical assessment has roots in the parametric statistics. The emphasis of the statistical tests are
mainly on the vector of post-fit residuals. The normal test of a single observation, test of a residual outlier and
test of the quadratic form of the residuals can be mentioned as examples of statistical assessments. The latter is
in fact the test of a posteriori variance factor given by equation (3.41) and is also a base for the generalized cross
validation (c.f. section 5.5.1). Vanicek and Krakiwsky (1982), (chapter 13), give a rather complete overview of
84
statistical tests used to assess the results of least-squares adjustment for geodetic applications.
This type of quality measures are indications for the capability of the solution to reconstruct the observations.
For gravity field determination from satellite data, it is not sufficient. The reason is, that even if the observations
at satellite altitude are well represented by the solution, it does not guaranty an acceptable representation on
the Earth’s surface. This issue is not trivial especially for regional gravity field solutions. Therefore, a regional
gravity field solution should be obtained in a way, that not only it passes statistical tests, but also other external
validations.
5.9.2 External validation
The quality of gravity field models should be tested against other sets of observations. As it is common in
practice, new gravity field solutions will be checked using other independent data sets such as GPS levelling,
absolute and relative gravimetry data and gravity anomalies as well as satellite altimetry data. In addition, the
new model can be checked using a previously known model which is accepted as a high-quality model. Here
the residuals are desired to be minimum on the Earth’s surface rather in the observation level. Gruber (2004)
gives more details on the concepts of validation strategies for satellite-based gravity field solutions. Gruber
et al. (2011) used orbit residuals as well as GPS-levelling to validate three global gravity field solutions based
on GOCE data. See also Gruber (2009), Tapley et al. (2005) and Ihde et al. (2010). In another study, Voigt
(2012) used astro-geodetic vertical deflections in Germany to validate GOCE gravity field models.
In the following chapter, we use the global geo-potential models GOCO03s and EGM2008 for the validation
of regional solutions.
5.9.3 Model-dependent evidences
No matter based on which data sets a gravity field is determined, the parameters should have the essential
characteristics of the model or the base functions used in the analysis step. For example, spherical harmonic
coefficients should fit the Kaula’s degree variances. Almost in all degree variance plots, the Kaula’s degree
variances are shown as an indication of agreement between the model and the expected behaviour (figure 3.5).
This expected compromise is even used for the regularization of global solutions known as Kauls’s stabilization.
While Kaula’s rule gives an insight into the expected spectral properties of SH coefficients, one should look
for spatial behaviours of scaling coefficients for SRBF. As we showed in figure 3.7, the scaling coefficients
αk should represent the spatial pattern of the gravitational potential or geoid according to the space-localizing
feature of SRBF. This is the idea of the PSC method explained in section 5.6. Bentel et al. (2013) also used this
fact as a measure of validation for their regional solutions using different SRBF.
Based on the discussions above, the regularization process for a reliable regional solution should satisfy the
following criteria:
• The observations’ residuals (e.g. the potential difference or the gravity gradients in the case of GRACE
and GOCE respectively) along the orbit of the satellite, i.e. kA11 x̂1 − l1 k, should be minimum.
• The synthesized geoid on the Earth’s surface should have minimum regional RMS with respect to a
high-resolution global gravity field model (say GOCO03s) or available terrestrial data sets.
• The estimated coefficients αk at grid point (φk , λk ) should have high correlation to the synthesized geoid
at these positions. In other words, αk should represent the shape of residual potential or geoid as much
as possible.
We will use these three measures to judge the quality of regional solutions and consequently the performance
of different regularization methods.
85
6 Numerical results
This chapter is devoted to the numerical implementation of the regional gravity field analysis using SRBF.
The main goal is to compare the performance of different regularization approaches, explained in the previous
chapter. In particular, the applicability of the proposed parameter-signal correlation (PSC) method is to be
assessed. To achieve this goal, we investigate the regional modelling in several test regions under different
conditions. Therefore the following questions are to be answered:
• What is the impact of different regularization methods on the regional solution?
• Does the quality of solutions significantly depend on the choice of grid points?
• Are regional solutions better than (or at least equivalent to) global solutions using SH (we use the geoid
RMS on the Earth’s surface as a measure for comparison)?
In the following section the specifications for regional gravity field modelling, such as test regions and grid
points will be defined. In section 6.2 gravity field modelling based on the data for a GRACE-type mission
will be addressed in a closed-loop simulation. Moreover, the regional solutions will be compared to a global
spherical harmonic solution based on the same data and imposed noise. Since it is beyond the scope of this PhD
thesis to discuss the technical details of dealing with real GRACE data, simulated GRACE data are used in this
section. However, to check the regional solutions based on real data, the regional gravity field modelling based
on real GOCE observations will be considered in 6.3. According to the drag-free system used on board the
GOCE satellite, much less data reduction and preparation are required compared to GRACE data. Moreover,
temporal corrections such as direct and indirect tide, polar tide and non-tidal variations are provided for GOCE
data which eliminate most of pre-processing efforts (Gruber et al., 2010).
6.1 Specifications of regional solutions
As we discussed in chapter 4, regional gravity field modelling using space localizing base functions includes
a collection of several choices which have to be made. Therefore it is not possible to define a unique way
for regional gravity field modelling. In the following computations, the emphasis is put on the choice of
the regularization parameter to compare the methods presented in chapter 5. The reason is the key role
of regularization in regional gravity field modelling. The job of regularization is to adjust different model
components to achieve the best possible approximation. Hence if the model is regularized appropriately, other
choices are not of great concern and can be kept rather simple. The regional gravity field modelling using SRBF
will be investigated in several test regions. The model specifications are defined in the following.
6.1.1 Test regions
The regional gravity field modelling will be considered in three test regions: Scandinavia, Central Africa
and South America. The main reason for choosing Scandinavia and Central Africa is the different coverage
of satellite data; while in regions with high latitude such as Scandinavia, satellite data are fairly dense, the
coverage is less dense in equatorial regions like Central Africa. This is due to the polar and near polar orbits
of GRACE and GOCE satellites. In addition, we also consider the regional modelling in South America due
to its rough gravity field along the Andes. It is an interesting region for geologists and geophysicists since the
world’s highest volcanoes are in the Andes. Thus, from the viewpoint of the signal content, it is a good region
to challenge the regional gravity field modelling.
Figure 6.1 displays the geographical extension of these regions on the global scale. In addition, the residual
geoid is also shown where the long wavelengths up to degree n = 30 are subtracted. The geographical
extensions of these regions are as follows:
86
6 Numerical results
Figure 6.1: The test areas for regional gravity field modelling based on satellite data: Scandinavia as a high
latitude region and Central Africa as an equatorial region. South America along the Andes will also
be considered due to its rough gravity field.
◦
◦
◦
◦
• Central Africa : −15 ≤ φ ≤ 15 and 5 ≤ λ ≤ 45 ,
◦
◦
◦
◦
• Scandinavia : 50 ≤ φ ≤ 75 and 0 ≤ λ ≤ 50 ,
◦
◦
◦
◦
• South America : −45 ≤ φ ≤ 15 and −85 ≤ λ ≤ −60 .
These limits will be considered as the model zone. The data and grid zones will be defined for each region
specifically.
6.1.2 Type of SRBF
According to the discussions in section 5.8, we confine ourselves to the Shannon kernel in the following
and show that it gives promising results using the proposed PSC method for the choice of the regularization
parameter. The maximum degree of expansion for the SRBF with the Shannon kernel will be Nmax = 130 and
Nmax = 300 for regional gravity field modelling based on simulated GRACE data and real GOCE observations,
respectively.
6.1.3 Type of grid points
The position of SRBF, i.e. (φk , λk , k = 1, ..., K), is a remarkable issue to be considered. This can be
determined along with other unknowns which results in non-linear parametrization. An alternative way is
to assume a set of fixed positions for the base functions. As mentioned in section 4.2.4, we follow the latter
method to maintain the linearity of the observation equations. Therefore a set of predefined grid points will be
used to locate the base functions. Our calculations show, that the use of different grid points does not affect the
quality of the regional solutions, provided that the grid points are distributed homogeneously (see 6.2.2). It only
affects the regularization process and the resulting regularization parameter. Therefore if the regularization is
performed correctly, the type of grid points is not a big concern in regional gravity field modelling. To show
this numerically, we use two different homogeneous point distributions on the sphere; the Reuter grid and the
Fibonacci grid. While the former gives equal-distant spacing, the latter results in equal areas on the surface of
the sphere. The mathematical formulation of these two grid points are given in section 4.2.4. Since the regional
modelling using these two grids are almost the same, the Fibonacci grid will be discussed only in section 6.2.2
to avoid repetition.
87
In this section, the performance of regional gravity field modelling will be checked based on the data from a
GRACE-like satellite mission. To have enough control over observation and model errors, the modelling is
done in a (pseudo) closed-loop simulation. In the first step, the potential differences between a pair of satellites
along GRACE-type orbits are synthesized using a global gravity field model. Furthermore, a realistic noise
model (white and coloured) is generated and added to the potential differences along the orbit.
Regional solutions are determined in the test regions using several regularization methods. The results will be
then compared to the input gravity field in the test regions. We assess the quality of the regional solutions based
on the RMS values of the reconstructed gravity fields on the Earth’s surface with respect to the input field. In
addition, a global gravity field solution using spherical harmonics is determined based on the same simulated
potential differences. Therefore the regional solutions can be directly compared to a global solution of the same
resolution. Figure 6.2 shows the simulation scheme used in this section.
Figure 6.2: Simulation scenario used to assess the performance of regional gravity field solution based on
satellite data. Several regional solutions in the test areas will be determined using SRBF to
compare different choices for the regularization. Furthermore, a global gravity field using spherical
harmonics will also be determined which makes it possible to directly compare the regional
solutions to the global solution.
6.2.1 Simulated data and noise
The simulated observations consist of synthesized potential differences VAB between satellites A and B. The
simulation scenario is the same as described in 3.3.2. The only difference is that here the maximum degree of
expansion in the synthesis is equal to Nmax = 120. This value matches the expected baseline resolution of
GRACE monthly solutions.
88
6 Numerical results
Figure 6.3: The geoid differences between the estimated global model using SH and the model GOCO03s
which is considered as the truth. The global RMS value is about 12 cm with the largest values near
equatorial areas. The test regions Scandinavia, Central Africa and South America along the Andes
are also shown in the map. The regional RMS values in these regions are 5.8, 21.7 and 22.7 cm,
respectively.
Based on this data set, a global gravity field model, using spherical harmonics is determined up to degree and
order Nmax = 120. Using this model, the gravity field will be synthesized in the test regions and the RMS
values will be calculated with respect to the true model GOCO03s. This gives an insight into the error budget in
each region when spherical harmonics are used in modelling. Therefore, the regional solutions using SRBF can
be directly compared to the spherical harmonic solution of an equivalent resolution. The number of unknown
SH coefficients is K = (120 + 1)2 − 3 or 14638 since the harmonics of degree zero and one are excluded. The
normal matrix therefore, has the size of 14638 × 14638 with the condition number of about 4.8 × 107 . The
covariance matrix of observations is assumed to be diagonal as if no information about the coloured noise is
available. The solution is estimated using equation (3.36) with no regularization.
Figure 6.3 shows the geoid differences between the estimated global model and GOCO03s which is considered
as the truth. As it can be seen, the largest deviations occur near equator where the satellite data are rather
sparse. The global RMS value for the geoid differences is 11.9 cm. The geoid differences in the test regions,
Scandinavia, Central Africa and South America along the Andes, which are displayed in the figure, are 5.8,
21.7 and 22.7 cm, respectively. In the following section, the regional solutions in the test regions shall be
obtained using SRBF with confinement of the data and base functions to the region boundaries. Compared to
the global spherical harmonic analysis, the number of data and base functions used in these test regions will be
approximately reduced by about 90%. Yet, equivalent or better solutions are expected on the regional scales
using SRBF. It should also be mentioned that the coloured noise generated for the global data set will be used
for regional solutions as well. Thus, the global solution and the following regional solutions are affected by the
same realization of coloured noise.
6.2.2 Regional solutions in Central Africa
The model zone in Central Africa is shown in figures 6.1 and 6.3. It is extended symmetrically around the
equator where the sampling of satellite data is less dense. The scope of gravity field modelling in this area is
to investigate the performance of SRBF in equatorial regions. The noisy data used for gravity field modelling
in this region are taken from the simulated global data, described in section 6.2.1. The potential differences
up to degree and order 30 are synthesized and subtracted from the simulated data, since the long wavelengths
89
of the gravitational potential cannot be modelled on regional scales. Therefore the observations contain the
frequencies between degree 30 and 120, in terms of spherical harmonics. Figure 6.4 shows the geoid heights
between degree 30 and 120 in Central Africa synthesized using the true model GOCO03s. Therefore, the goal
is to model this field using SRBF as precise as possible. The difference between the model GOCO03s and the
global SH model described in previous section, is also shown in figure 6.4 in terms of geoid heights. The geoid
RMS in this region is about 22 cm with sharp stripes in the edges of the region.
Figure 6.4: Left: Geoid heights in Central Africa, between degrees 30 and 120, synthesized using the global
model GOCO03s. The maximum and minimum values within this region are about 6.5 and −5.2 m
respectively. Right: The geoid difference, in Central Africa, between GOCO03s and the spherical
harmonic model based on the simulated data explained in section 6.2.1. The geoid RMS is 21.7 cm
in this region.
As explained in chapter 4, the bounds of the data and grid zones should be defined appropriately. This is due
to the edge effects caused by confinement of data and base functions to a region. For the extension of the data
◦
zone, equations (4.18) is used with Nmin = 30, φm = 0 and h = 500 km. Therefore the data zone for Central
◦
Africa will be extended 6 beyond the model zone. The total number of observations within the data zone will
be about 16700 which is 3% of the total observations on the global scale. Furthermore, the grid extension is
◦
set to be 5 . The number of unknowns inside the grid zone depends on the type of grid points used for the
distribution of the base functions. Since we use the Reuter and Fibonacci grids which are homogeneous grids
the number of base functions differ very slightly and is around 1400. Compared to about 14000 SH on the
global scale, the number of unknowns is reduced by 90%. Finally, the SRBF with Nmax = 130 and with the
Shannon kernel are used for the inversion of the simulated data. Figure 6.5 shows the boundaries of the model,
the data and the grid zones for regional modelling in Central Africa.
90
6 Numerical results
Figure 6.5: The model zone (red) ,the data zone (blue) and the grid zone (black) for the regional gravity field
◦
solution in Central Africa. The data zone is extended 6 beyond the model zone and the grid zone
◦
is extended 5 beyond the data zone.
Based on this setup, the corresponding design and normal matrices are computed. The condition number of the
normal matrix is about 9.9 × 1018 which reveals a strong ill-posedness as expected. As proposed in section
5.7, one can use equations (5.77) or (5.88) to evaluate an initial value for the regularization parameter. For this
region, these values will be about 3 × 1023 and 1.3 × 1023 using (5.77) and (5.88), respectively. This shows that
these two methods lead, more or less, to the same values. We set the initial value equal to 2 × 1023 and search
for the optimal regularization parameter in the neighbourhood of this value with radius of 102 . The summary
of the model setup for regional gravity field modelling in this region is given in table 6.1.
According to the set-up mentioned in the table 6.1, two groups of solutions are obtained using the Reuter
and Fibonacci grids. Each group consists of four different solutions based on four different parameter choice
methods for regularization. All solutions are obtained using the following relation:
x̂ = (AT Pl A + γ 2 I)−1 AT Pl δl.
(6.1)
The only difference between the solutions is the criterion used to choose γ 2 . These criteria (explained in section
5.5) are: The variance component estimation (VCE), the generalized cross validation (GCV), the L-curve
analysis and the proposed parameter-signal correlation (PSC). The weight matrix Pl is assumed to be a diagonal
matrix. In other words, we assume that the observation noise is white because there is no information available
about the colour of noise in real-life experiments. The reduced observation vector δl is obtained using (4.12)
where the long wavelengths up to degree 30 are subtracted. Therefore the solution x̂ shall be used to represent
the gravitational potential (and other functionals) between frequencies 30 and 120. To compare the solutions
and judge their quality, we use the three conditions explained at the end of section 5.9. Thus, the residuals at
orbit altitude, the residuals on the Earth’s surface and the correlation between the estimated coefficients and a
reference field shall be considered.
The summary of the results for the regional solutions in Central Africa using the Reuter grid is given in table
6.2. The results for the same solutions but using Fibonacci grid is given in table 6.3. As it can be seen, in all
cases, the RMS values at orbit level are closely the same. The statistical test on the a posteriori variance factor
σˆ02 are also passed in all cases. This means that all parameter choice methods can provide good results when
no downward continuation is included. Nevertheless, the results are very different when the solutions are to be
compared on ground level. The proposed PSC method, gives the best results compared to other regularization
methods. The L-curve analysis provides rather the same results as the PSC with slightly larger RMS values
for the reconstructed fields on the Earth’s surface. On the other hand, the VCE and GCV approaches result in
significantly different RMS values on the Earth’s surface. This is also clear by comparing the regularization
parameters. While VCE and GCV methods give parameters in the order of 1021 , the regularization parameters
91
Model specification
Remarks
◦
◦
◦
◦
the model zone: −15 ≤ φ ≤ 15 , 5 ≤ λ ≤ 45
Geographical limits
the data zone: −21 ≤ φ ≤ 21 , − 1 ≤ λ ≤ 51
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: −26 ≤ φ ≤ 26 , − 6 ≤ λ ≤ 56
observation type: potential difference at orbit altitude
frequency content: above 30 (SH)
Observations
number of observations: I = 16728
standard deviation: 2 × 10−3 m2/s2
weight matrix: Pl = (2 × 10−3 m2/s2 )−2 × I
the a priori variance factor: σ02 = 1
The base functions
type of SRBF: Shannon (Nmax = 130)
number of base functions: K = 1389
size: 1389 × 1389
The normal matrix N
condition number: 9.9 × 1018
largest singular value: s21 = kNk = 2.9 × 1028
Initial regularization parameter
using (5.77): γ 2 = 3.2 × 1023
using (5.88): γ 2 = 1.3 × 1023
Table 6.1: Specifications of the regional modelling in Central Africa. The number of unknowns is in fact the
number of grid points. In this table, 1389 refers to the number of points on the Reuter grid. For the
Fibonacci grid, this number is 1380.
for the L-curve and the PSC methods are one and two orders of magnitude larger. Obviously the VCE and GCV
methods do not provide sufficient regularization for regional gravity field modelling based on satellite data. If
the regional modelling based on terrestrial or airborne data (with no considerable downward continuation)
were desired, these methods could be satisfactory. The L-curve method requires a compromise between the
minimization of the post-fit residuals and the norm of the solution. Similarly, the PSC method enforces the
solution to have the expected geometry by correlating the coefficients with a background model1 . That is why
the correlation between the coefficients and the signal is maximum (97.7%) in case of the PSC method and is
nearly followed by the L-curve analysis with (97.3%). This correlation for the VCE and GCV methods is about
10% less and amounts to 91% and 87% respectively.
Figure 6.6 shows the estimated coefficients obtained from the PSC regularization approach2 . It can be compared
to the regional geoid shown in figure 6.4. As it can be seen, the coefficients reveal the general shape of the geoid
(between frequencies 30 and 120).
1
For the numerical computations in this chapter, we used the model EGM2008 to evaluate the potential values dVk at grid locations.
See Table 5.1 for more details.
◦
◦
2
For a better visualization, the coefficients are interpolated to a dense regular grid with cell size of 0.1 × 0.1
92
6 Numerical results
Figure 6.6: The dimensionless estimated coefficients obtained from the PSC regularization approach. For better
◦
◦
illustration, the coefficients are interpolated on a dense regular grid with cell size of 0.1 × 0.1 .
The coefficients show the general shape of geoid shown in figure 6.4. The correlation coefficient is
about 97.7%.
To assess the quality of the solutions in terms of residuals on the Earth’s surface, the geoid heights are
synthesized using the estimated coefficients and a set of SRBF with the Shannon kernel. Figure 6.7 illustrates
the geoid differences between the regional solutions and the geopotential model GOCO03s. The solutions
obtained using the Reuter grid and from four different approaches for the choice of the regularization parameter.
The same group of solutions but using the Fibonacci grid is shown in figure 6.8.
Summary and concluding remarks for regional solutions in Central Africa
Eight regional solutions were determined in Central Africa using four different regularization methods and two
types of grid points. The results of the solutions and the conclusion after comparisons can be summarized as
follows:
• Among the four solutions using different parameter choice methods for each grid type, the PSC gives
the best results with the least geoid RMS. The L-curve analysis also provides a rather promising solution
with a geoid RMS slightly more than the PSC. The VCE and GCV methods, have RMS values about 3
times larger than PSC and L-curve.
• The results obtained from the Fibonacci grid are almost the same as the Reuter grid. No significant
differences are seen when the two grids are compared. Hence these two grid points (and other grid types
with homogeneous point distribution) can be used alternatively. In the following sections, the Fibonacci
grid will not be considered for brevity.
• All solutions can be compared to the global spherical harmonic solution shown in figure 6.4 (left). The
SH solution gives a geoid RMS of about 21.7 cm in Central Africa which is comparable to the regional
solutions obtained from the VCE and GCV methods. On the other hand, the L-curve with geoid RMS
of 13 cm and, in particular, the PSC methods with geoid RMS of 10 cm provide much better results
with much less stripes compared to the global SH solution. The results also indicate that the north-south
GRACE stripes are significantly reduced as a result of using the PSC method.
93
Figure 6.7: Geoid differences between the global model GOCO03s and regional solutions in Central Africa
using four different regularization methods: the variance component estimation (top-left), the
generalized cross validation (top-right), the L-curve analysis (bottom-left) and the proposed PSC
(bottom-right). The best regional geoid RMS is obtained using PSC. The L-curve analysis gives
slightly more RMS. The VCE and GCV methods yield significantly larger geoid RMS. These
solutions are obtained using the Reuter grid.
Regularization
method
γ2
RMS
(orbit, m2/s2 )
RMS
(Earth’s surface, cm)
test on
σ̂02 (95%)
correlation of
signal and parameters
VCE
2.417 × 1021
0.0016
28.8
passed
91.9%
GCV
7.948 ×
1020
0.0016
38.8
passed
87.5%
L-curve
5.084 × 1022
0.0017
13.2
passed
97.3%
PSC
2.129 × 1023
0.0018
10.6
passed
97.7%
Table 6.2: Summary of the regional solutions in Central Africa and their quality measures. The solutions are
obtained using the Reuter grid. The best results are obtained using the proposed parameter-signal
correlation method where all three quality measures are satisfactory. The L-curve method provides
also satisfactory results which are only slightly different from the PSC method.
94
6 Numerical results
Figure 6.8: The geoid differences between the global model GOCO03s and the regional solutions in Central
Africa using four different regularization methods: the variance component estimation (top-left),
the generalized cross validation (top-right), the L-curve analysis (bottom-left) and the proposed
PSC (bottom-right). The best regional geoid RMS is obtained using PSC method. The L-curve
analysis gives slightly more geoid RMS. The VCE and GCV methods yield significantly larger
geoid RMS. These solutions are obtained using the Fibonacci grid.
Regularization
method
γ2
RMS
(orbit, m2/s2 )
RMS
test on
σ̂02 (95%)
correlation of
VCE
2.354 × 1021
0.0016
28.9
passed
91.6%
GCV
7.937 ×
1020
0.0016
37.9
passed
87.2%
L-curve
5.078 × 1022
0.0017
13.3
passed
97.1%
PSC
2.558 × 1023
0.0018
10.7
passed
97.5%
Table 6.3: Summary of the solutions in Central Africa and their quality measures. The solutions are obtained
using the Fibonacci grid. The best results are obtained using the proposed PSC method where all
three quality measures are satisfactory.
95
6.2.3 Regional solutions in Scandinavia
To consider the performance of regional gravity field modelling as well as different regularization methods, the
regional modelling should be checked under different conditions and test areas. In this section, the procedure
explained in the previous section for Central Africa will be repeated for Scandinavia. The main reason to
choose this area is its high latitude. In such areas, the satellite missions such as GRACE, GOCE and GRACE
Follow-on collect more observation so that the sampling is rather dense.
◦
The desired model zone in Scandinavia is shown in figures 6.1 and 6.3 with geographical bounds 50 ≤ φ ≤
◦
◦
◦
75 and 0 ≤ λ ≤ 50 . The description of the simulated data set and imposed noise is the same as explained in
previous section. The geoid in Scandinavia between frequencies 30 and 120, in terms of spherical harmonics, is
the target field to be modelled using SRBF. This field is shown in figure 6.9 (left) which is synthesized using the
global model GOCO03s. In this region the geoid varies approximately from -4 to 5 m (the frequencies less than
n = 30 are subtracted). Furthermore, the geoid difference between GOCO03s and the SH model determined in
section 6.2.1 is also shown in this figure. The total RMS is about 6 cm with large stripes in the southern part of
the area.
Figure 6.9: Left: Geoid heights in Scandinavia, between degrees 30 and 120 synthesized using the global model
GOCO03s. The maximum and minimum values within this region are about 4.8 m and −3.6 m,
respectively. Right: The geoid differences in Scandinavia between GOCO03s and the spherical
harmonic model based on the simulated data explained in section 6.2.1. The geoid RMS is about
6 cm in this region. The north-south GRACE stripes are also visible especially in the southern part
of the region.
To model this regional field based on the simulated data and using SRBF, the boundaries of the data and the
grid zone have to be defined. Similar to the definition of these zones in Central Africa, the extension of data
◦
◦
and grid zones are equal to 6 and 5 , respectively. These three zones in Scandinavia are illustrated in figure
6.10.
96
6 Numerical results
Figure 6.10: The model zone (red), the data zone (blue) and the grid zone (red) for regional modelling in
◦
◦
Scandinavia. The grid and data zones are extended by 6 and 5 beyond the model and data zones,
respectively.
The number of observations inside the data zone is about 25800 with a total number of over 1130 base functions
(grid points). The summary of the observation equations as well as the model characteristics is given in table
6.4.
Model specification
Remarks
◦
◦
◦
◦
the model zone: 50 ≤ φ ≤ 75 , 0 ≤ λ ≤ 50
Geographical limits
the data zone: 44 ≤ φ ≤ 81 , − 6 ≤ λ ≤ 56
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: 39 ≤ φ ≤ 86 , − 11 ≤ λ ≤ 61
observation type: potential differences at orbit altitude
Observations
The base functions
size: 1136 × 1136
The normal matrix N
using (5.77): γ 2 = 1.1 × 1025
using (5.88): γ 2 = 4.4 × 1023
Table 6.4: Specifications of the regional modelling in Scandinavia. The number of unknowns which is in fact
the number of grid points is 1136 in this table. This number refers to the number of points on the
Reuter grid.
97
Figure 6.11: The geoid differences between the global model GOCO03s and the regional solutions in
Scandinavia using four different regularization methods: the variance component estimation
(top-left), the generalized cross validation (top-right), the L-curve analysis (bottom-left) and the
proposed PSC (bottom-right). The best regional RMS is obtained using the PSC method. The
L-curve gives slightly more geoid RMS. The VCE and GCV methods yield significantly larger
RMS. These solutions are obtained using the Reuter grid.
γ2
RMS
(orbit, m2/s2 )
RMS
test on
σ̂02 (95%)
correlation of
VCE
2.426 × 1021
1.8 × 10−3
15.4
passed
95.2%
GCV
2.606 × 1021
1.8 × 10−3
15.3
passed
95.2%
1023
10−3
10.3
passed
96.0%
8.1
passed
96.2%
Regularization
method
L-curve
1.003 ×
PSC
4.608 × 1023
1.8 ×
2 × 10−3
Table 6.5: Summary of the regional solutions in Scandinavia with their quality measures. The solutions are
also satisfactory results which are just slightly different from the PSC method.
Finally, the solutions are obtained using equation (6.1) and four methods for the choice of the regularization
parameter. The results of the solutions for the Reuter grid are given in table 6.5. It can be evidently seen that all
solutions pass the statistical tests at the observation level. That is, the test on the a posteriori variance factor is
98
6 Numerical results
passed in all cases and the post fit residuals at orbit level have more or less the same RMS values. On the other
hand, the geoid RMS on ground level are different. The VCE and GCV methods provide almost the same geoid
RMS values. It is about 15 cm which, for these two methods, is significantly improved compared to the regional
solutions in Central Africa. The reason is the availability of more observations in high-latitude regions such as
Scandinavia. The L-curve analysis and the PSC methods result in less geoid RMS on ground level which is
about 10 cm and 8 cm, respectively. The geoid differences on the Earth’s surface using different regularization
approaches are shown in figures 6.11. Due to the similarity of the results obtained from the Reuter and the
Fibonacci grids, the results of the Fibonacci grid are not shown anymore.
The estimated scaling coefficients are displayed in figure 6.12. The estimated coefficients explicitly reveal the
shape of geoid heights above n = 30 (c.f. figure 6.9).
Figure 6.12: The dimensionless estimated coefficients obtained from the PSC regularization approach. For
◦
better illustration, the coefficients are interpolated on a dense regular grid with a cell size of 0.1 ×
◦
0.1 . The coefficients reveal the general shape of the geoid shown in figure 6.9. The correlation
coefficient is about 96.2%.
Summary and concluding remarks for the regional solutions in Scandinavia
In Scandinavia, four regional solutions were determined based on simulated GRACE-type observations using
SRBF. The solutions are obtained using four different methods for the choice of the regularization parameter.
The results of modelling and comparisons can be summarized as follows:
• Among the regularization methods, the PSC method results in the least geoid RMS values and give the
most promising solution. The L-curve analysis leads to nearly the same results compared to the PSC
method. The VCE and GCV give rather the same geoid RMS values but considerably larger than the first
two methods.
• Compared to the regional solutions in Central Africa, the solutions in Scandinavia have less geoid RMS
values. This is due to the fact that more observations are available in this region according to its high
latitude.
• All regional solutions give larger geoid RMS compared to the global SH solution. Only the PSC method
provides approximately the same geoid RMS (8 cm) compared to the global solution using spherical
harmonics (6 cm).
99
• It can be concluded that in high-latitude regions, spherical harmonics perform optimally. Nevertheless,
the regional solution which is regularized using the PSC method can provide a comparable accuracy with
much less computational burden. This is a great advantage especially if more data than a month are
included.
6.2.4 Regional solutions in South America
The last test area for the investigation of the regional gravity field solution, is South America along the Andes.
In this area, the gravity field is very rough and has significant spatial changes across the mountain chains in
east-west direction. The maximum and minimum values of the geoid are about -14 and 11 m, respectively
(between SH frequencies 30 and 120). This rather big changes occur within a few hundred kilometres. In
addition, the world’s largest volcanoes are in this region which makes it an interesting area for geophysical
and geological studies. Thus, this region can be considered as a challenging test area for regional gravity field
modelling from satellite data.
Figure 6.13: Left: Geoid heights in South America along the Andes, between degrees 30 and 120, synthesized
using the global model GOCO03s. The maximum and minimum values within this region are
about 11.1 and −14.1 m respectively. Right: The geoid difference, in South America, between
the model GOCO03s and the spherical harmonic model based on the simulated data explained in
section 6.2.1. The geoid RMS is about 23 cm in this region. The north-south GRACE stripes are
also visible especially in the west part of the region.
◦
◦
The model zone in this region is shown in figures 6.1 and 6.3 with geographical bounds −45 ≤ φ ≤ 15 and
◦
◦
−85 ≤ λ ≤ −60 . The description of the simulated data set and imposed noise is the same as explained in
previous sections. The geoid in the Andes, between frequencies 30 and 120, is to be modelled in this region
using SRBF. This field is shown in figure 6.13 (left) which is synthesized using the global model GOCO03s.
Furthermore, the geoid difference between GOCO03s and the SH model determined in section 6.2.1 is also
shown in this figure. The total RMS in this region is about 23 cm with large stripes in the west of the area. The
boundaries of the data and grid zones are defined similar to the definition of these zones in Central Africa and
◦
◦
Scandinavia with the extension of 6 and 5 . These three zones in the Andes are illustrated in figure 6.14.
100
6 Numerical results
Figure 6.14: The model zone (red), the data zone (blue) and the grid zone (red) for regional modelling in South
◦
◦
America along the Andes. The grid and data zones are extended 6 and 5 beyond the model and
data zones, respectively.
The description of observation equations and the model setup is given in table 6.6.
Model specification
Remarks
◦
◦
◦
◦
the model zone: −45 ≤ φ ≤ 15 , − 85 ≤ λ ≤ −60
Geographical limits
the data zone: −51 ≤ φ ≤ 21 , − 91 ≤ λ ≤ −54
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: −56 ≤ φ ≤ 26 , − 96 ≤ λ ≤ −49
observation type: potential differences at orbit altitude
Observations
The base functions
size: 1520 × 1520
The normal matrix N
using (5.77): γ 2 = 4.3 × 1023
using (5.88): γ 2 = 1.5 × 1023
Table 6.6: Specifications of the regional modelling in South America along the Andes. The number of
unknowns or the number of grid points is 1520 in this table. This number refers to the number
of points on the Reuter grid.
101
The solutions are obtained using equation (6.1) and four different regularization parameters. The results are
very similar to those obtained in Central Africa. The proposed PSC method results in the most promising
solution compared to other approaches for the choice of the regularization parameters. Figure 6.15 shows
the estimated coefficients obtained from the PSC regularization approach. It can be compared to the regional
geoid shown in figure 6.13. As it can be seen, the coefficients reveal the general shape of the geoid (between
frequencies 30 and 120).
Figure 6.15: The dimensionless estimated coefficients obtained from the PSC regularization approach. For
◦
better illustration, the coefficients are interpolated on a dense regular grid with cell size of 0.1 ×
◦
0.1 . The coefficients reveal the general shape of the geoid shown in figure 6.13. The correlation
coefficient is about 96.9%.
The results of regional modelling in South America along the Andes on the Reuter grid is given in table 6.7.
The same calculations were performed using the Fibonacci grid (results not shown here) which led to the same
numerical results with no statistically significant differences. This indicates that as long as the distribution of
grid points is homogeneous enough, the type of grid is not a great concern and does not affect the quality of
regional solutions. Furthermore, the geoid differences between the regional solutions and the global model
GOCO03s are shown in figures 6.16 for the Reuter grid. As it can be seen, the best results are obtained using
the PSC method followed by the L-curve analysis. The geoid RMS values for the GCV and the VCE are nearly
the same but still far from the results obtained using the PSC and L-curve analysis.
102
6 Numerical results
γ2
RMS
(orbit, m2/s2 )
RMS
test on
σ̂02 (95%)
correlation of
VCE
9.945 × 1020
0.0016
45.3
passed
94.6%
GCV
9.152 × 1020
0.0016
46
passed
94.5%
L-curve
1.844 ×
1022
0.0016
25.4
passed
96.6%
PSC
8.875 × 1022
0.0017
19.7
passed
96.9%
Regularization
method
Table 6.7: Summary of the regional solutions in the Andes with their quality measures. The solutions are
also satisfactory results which are slightly different from the PSC method.
Figure 6.16: The geoid differences between the global model GOCO03s and the regional solutions in South
America using four different regularization methods. From left to right: the variance component
estimation, the generalized cross validation, the L-curve analysis and the proposed PSC method.
The best regional RMS is obtained using the PSC. The L-curve analysis gives slightly more RMS.
The VCE and GCV methods yield significantly larger RMS. Results are for the case of Reuter
grid.
Summary and concluding remarks for the regional solutions in South America along the
Andes
In the area of the Andes, four regional solutions were determined based on simulated GRACE-type observations
using SRBF. The solutions are obtained using the Reuter grid and four different methods for the choice of the
regularization parameter. The results of modelling and comparisons can be summarized as follows:
• Among the regularization methods, the PSC method results in the least geoid RMS values and give the
most promising solution. The L-curve analysis leads to nearly the same results compared to the PSC
method. The VCE and GCV give rather the same geoid RMS values but considerably larger than the first
two methods.
• Compared to the regional solutions in Central Africa and Scandinavia, the solutions in the Andes have
larger geoid RMS values. This is due to the fact that less observations are available in this region
compared to Scandinavia.
103
• The regional solutions using the PSC and L-curve methods provide better geoid RMS compared to
the global solution using spherical harmonics. For the VCE and GCV methods, the largest deviations
between the regional solutions and the model GOCO03s are visible in the western part of the region
around the equator. These RMS values are much larger than the global solution shown in figure 6.13
(right). Thus the VCE and GCV methods cannot provide sufficient regularity for the regional solutions
based on satellite data when the base functions have no measure of regularity (c.f. section 5.8).
104
6 Numerical results
In the previous section, the performance of different methods for the choice of the regularization parameter for
regional gravity field modelling was investigated based on simulated GRACE-type data. Results indicate that
the proposed PSC method gives promising solutions compared to other methods. Although the simulated data
were corrupted with a realistic coloured noise, it is however desired to check the applicability of the method
when real data are included. For this purpose, the real GOCE gravity gradients will be used in this section. In
addition, GOCE data are more appropriate to be used for regional modelling than GRACE-type observations.
The long wavelengths of the gravity field, i.e. global features (n < 30), cannot be accurately determined
using GOCE gravity gradients. The reason is the poor quality of GOCE gravity gradients in low-degree
parts of the field. As a result, the long wavelengths of GOCE-only solutions are not comparable to those of
GRACE-only solutions. Instead, GOCE data are very sensitive in the measurement bandwidth (approximately
between degrees 30 and 250 in terms of spherical harmonics). This means, GOCE gradiometry is very useful
for the determination of medium and short wavelengths of the gravity field (30 < n < 250). In the spatial
domain, this is equivalent to regional areas from about 1000 km to local features down to almost 200 km.
6.3.1 GOCE data and functional model
The real GOCE data used in this thesis are gravity gradients observed by the GOCE gradiometer. These data
cover a time span of two months (October and November 2010) and are part of GOCE level-2 data product.
In addition, GOCE kinematic orbit data are used to locate gravity gradients along the orbit. For a complete
description of GOCE level-2 product see GOCE Level 2 Product Data Handbook (Gruber et al., 2010). Two
months of data, are the minimum amount of data for high-resolution gravity field recovery based on GOCE data.
The use of more data will improve the quality of the final solution. Nevertheless, we confined our calculations
to two months of GOCE data only which are sufficient to fulfil the aims of this thesis.
In order to use GOCE observations, it is necessary to note the following issues:
• From six components of gradient tensor, only four components can be measured with high sensitivity.
These components are: Vxx , Vyy , Vzz and Vxz . Other components, i.e. Vxy and Vyz , are of less
quality (Bouman et al., 2011, Stummer et al., 2008). According to equation (2.31), all gravity gradient
components in LNOF are linear combinations of gravity gradients in GRF (c.f. figure 2.3). Direct rotation
of gravity gradients from GRF into LNOF without additional processing would project the larger error
of the less accurate gravity gradients into the accurate components in the LNOF. In other words, high
accurate components are mixed with less accurate ones to provide the gravity gradient tensor in the
LNOF. A way out of this problem is, to compute Vxy and Vyz based on an a prior gravity field model and
use the computed values instead of observed values (Gruber et al., 2010). An alternative way is to set
up the observation equations in the GRF, instead of the LNOF. This means that the equations are rotated
rather than the observations. Therefore it will be possible to use the original GOCE measurements in
the observation vector. Hence, one can employ (2.34) instead of (2.31) to avoid the undesired mixture of
accurate measurements with less sensitive ones. See Bouman (2007) for more details on this issue.
• The high sensitivity of GOCE measurements is achievable in a specific frequency band which is known as
measurements bandwidth (MBW). This bandwidth includes the frequencies from about 0.005 to 0.04 Hz
which approximately corresponds to the spherical harmonic degree n = 30 up to n = 2201 . This implies
that the lower degrees or long wavelengths of the gravitational potential cannot be precisely measured
based on GOCE gradiometer data. Therefore it is necessary to calibrate GOCE observations using a
state-of-the-art gravity field model. The algorithm is described in Gruber et al. (2010) for EGG-TRF-2
product. See also Brieden and Müller (2011) for more details.
We use equation (2.34) as the observation equation, i.e. the equations are rotated rather than the observations.
Moreover, we use filtered GOCE measurements provided in the GRF, that is, the observations are externally
1
According to Gruber et al. (2010), the official measurement bandwidth ranges from 0.005 to 0.1 Hz. However the usable part is
limited to approximately 0.04 Hz in the upper bound.
105
calibrated using a global gravity field model. Brieden and Müller (2011) give more details on the concepts used
for GOCE data validation.
In section 2.3, the relation between gravity gradients in the Earth fixed frame and the LNOF were given using
(2.35). It was also mentioned, that the first and second derivatives of the gravitational potential V change with
the type of base functions used for the representation. Here in this section, we determine these derivatives,
i.e. Vr , Vφ and Vλ as well as Vrr , Vrφ , Vφφ , Vφλ and Vλλ in terms of SRBF. The general form of gravity field
representation using SRBF is given by
V (ri , φi , λi ) =
K
∞
GM X X R n+1
(2n + 1)bn Pn (s)
αk
( )
R
ri
k=1
(6.2)
n=0
where s is the spherical distance defined as:
s = sin φ sin φk + cos φ cos φk cos(λ − λk ).
(6.3)
The first derivatives can be expressed using the following

K
∞ R
P

GM P


α
V
(r
,
φ
,
λ
)
=
−
( )n+2 (2n + 1)(n + 1)bn Pn (s)
r
i
i
i
k

2

R
ri

n=0
k=1


K
∞ R
P
GM P
Vφ (ri , φi , λi ) =
αk
( )n+1 (2n + 1)bn sφ Pn0 (s)

R
ri
n=0
k=1



K
∞ R
P
P

GM

Vλ (ri , φi , λi ) =
αk
( )n+1 (2n + 1)bn sλ Pn0 (s)

R k=1 n=0 ri
(6.4)
in which sφ and sλ are the directional derivatives of the spherical distance s given by

ds

sφ =
= cos φ sin φk − sin φ cos φk cos(λ − λk )
dφ

sλ = ds = − cos φ cos φk sin(λ − λk ).
dλ
(6.5)
The components of the gradient tensor can be obtained by taking the derivatives of (6.4). Thus, the second
derivatives are

K
∞ R
P
GM P


V
(r
,
φ
,
λ
)
=
( )n+3 (2n + 1)(n + 1)(n + 2)bn Pn (s)
α
rr
i
i
i
k


R3 k=1 n=0 ri



K
∞ R

P
GM P



Vφφ (ri , φi , λi ) =
αk
( )n+1 (2n + 1)bn [sφφ Pn0 (s) + s2φ Pn00 (s)]


R k=1 n=0 ri



K
∞ R

P
GM P


αk
( )n+1 (2n + 1)bn [sλλ Pn0 (s) + s2λ Pn00 (s)]
Vλλ (ri , φi , λi ) =
R k=1 n=0 ri
K
∞

V (ri , φi , λi ) = − GM P α P ( R )n+2 (2n + 1)(n + 1)bn s P 0 (s)

rφ
k
φ n


R2 k=1 n=0 ri



K
∞ R

P
GM P


V
(r
,
φ
,
λ
)
=
−
α
( )n+2 (2n + 1)(n + 1)bn sλ Pn0 (s)

i
i
i
rλ
k


R2 k=1 n=0 ri



K
∞

V (r , φ , λ ) = GM P α P ( R )n+1 (2n + 1)b [s P 0 (s) + s s P 00 (s)]

n φλ n
φλ i i i
k
φ λ n
R k=1 n=0 ri
(6.6)
and noting that Vrλ = Vλr , Vrφ = Vφr and Vφλ = Vλφ due to the fact that the gradient tensor is symmetric.
The second derivatives of the spherical distance s, i.e. sφφ , sφλ and sλλ are obtained by taking the directional
derivatives of (6.5)
106
6 Numerical results

d2 s


= −[sin φ sin φk + cos φ cos φk cos(λ − λk )] = −s
s
=
φφ


dφ2


2
d s
s
=
= sin φ cos φk sin(λ − λk )] = sλφ
φλ

dφdλ


2


s = d s = − cos φ cos φ cos(λ − λ ).
k
k
λλ
dλ2
(6.7)
Pn0 (s) and Pn00 (s) are the first and second derivatives of the Legendre polynomials Pn (s) with respect to s.
Having obtained the gravity gradients using equation (6.6), the equations can now be rotated into the GRF
frame using (2.34). Finally the design matrix will be set up by differentiating (2.34) with respect to the unknown
coefficients αk :
GRF
∂Vjk
∂αk
= R̂
LN OF
∂Vjk
∂αk
R̂T
(6.8)
where R̂ is the rotation matrix which is defined in section 2.3.2.
6.3.2 Setting up the regional models
Regional gravity field modelling based on GOCE data will be investigated in the same test regions explained
in section 6.1. The limits of the model zone are exactly the same as before. The extension of the data and
◦
grid zones is 3 beyond the model and data zone respectively. The Shannon kernel with Nmax = 300 is
used for the analysis of the regional solutions. The maximum degree of expansion is chosen to be above the
expected resolution of the GOCE gravity field models to reduce aliasing effects. Nevertheless, the synthesis of
the regional solutions will be restricted to Nmax = 240 since the solutions for the higher degrees are too noisy.
As it is shown in the previous section, the type of grid points does not noticeably change the quality of the
regional solutions. Therefore we only use the Reuter grid and the Fibonacci grid is not considered anymore.
The observations are the Vzz component measured by the GOCE gradiometers in the GRF. The data span a
time period of two months with sampling rate of 1 s. A moving average filter is applied to down sample the
observations to the sampling rate of 5 s. The averaging filter reduces the size of the design matrix and decreases
the cost of computation. In addition, the observation noise will also be reduced due to the low-pass features of
the averaging filter. To set the weight matrix, the standard deviation of observations are assumed to be about
2 × 10−12 E. The long wavelengths of Vzz up to degree n = 30 are computed using the geopotential model
GOCO03s and subtracted from the observations. Therefore the data contain the frequencies above degree
30. Finally, the four methods for the choice of regularization parameters (VCE, GCV, L-curev and PSC) will
be used for the inversion of the regional solutions. The regional solutions will be compared to two existing
global gravity field models, the EGM2008 and the GOCO03s. The former contain no information from GOCE
mission and its high frequency parts are mainly dependent on terrestrial data. The latter, on the other hand, is a
combined model based on GRACE and GOCE observations with no terrestrial data included.
6.3.3 Regional solutions based on GOCE data
Regional solutions in Central Africa
The specifications of the regional setup for Central Africa are given in table 6.8. The total number of the gravity
gradients Vzz is about 27000 inside the data zone. With the total number of almost 6000 unknown parameters,
the size of the design matrix is about 27000 × 6000.
The condition number of the normal matrix is around 4 × 1019 revealing the strong ill-posedness of the regional
model. Table 6.9 summarizes the characteristics of the solutions.
107
Model specification
Remarks
◦
◦
◦
◦
the model zone: −15 ≤ φ ≤ 15 , 5 ≤ λ ≤ 45
Geographical limits
the data zone: −18 ≤ φ ≤ 18 , 2 ≤ λ ≤ 48
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: −21 ≤ φ ≤ 21 , − 1 ≤ λ ≤ 51
observation type: Vzz at orbit altitude
Observations
standard deviation: 2 × 10−12 Etvs
weight matrix: Pl = (2 × 10−12 Etvs)−2 × I
The base functions
size: 6015 × 6015
The normal matrix N
using (5.77): γ 2 = 2.5 × 1021
using (5.88): γ 2 = 2.8 × 1020
Table 6.8: Specifications of the regional modelling in Central Africa.
γ2
orbit RMS
(Etvs)
surface RMS
(EGM2008, cm)
surface RMS
(GOCO03s, cm)
correlation of
VCE
5.519 × 1022
2.3 × 10−12
46.5
37.0
90.0%
GCV
4.523 ×
1023
10−12
36.4
22.6
96.6%
L-curve
3.273 × 1023
2.4 × 10−12
37.6
24.6
96.3%
Regularization
method
2.4 ×
PSC
1.649 × 1024 2.4 × 10−12
34.1
19.4
97.1%
Table 6.9: Summary of the regional solutions in Central Africa and their quality measures. The solutions are
obtained using the Reuter grid. The RMS values on the Earth’s surface are obtained with respect to
two global models EGM2008 and GOCO03s
The PSC method gives the largest regularization parameter with the minimum surface RMS values. The
correlation of the PSC-derived coefficients with geoid heights is maximum. The L-curve analysis and the GCV
methods result in more or less the same results. The GCV method gives closely the same results as the L-curve
and the PSC. The VCE leads to the largest value of surface RMS showing that the amount of regularization by
this method, compared to others, is not sufficient. The interesting fact is that all methods provide nearly the
same RMS values at orbit altitude. The RMS values on the Earth’s surface are given with respect to two global
models EGM2008 and GOCO03s. In all cases, the RMS values with respect to the global model GOCO03s,
are smaller than those with respect to EGM2008. The reason is the absence of GOCE data in the EGM2008.
108
6 Numerical results
Figure 6.17: The differences between regional solutions in Central Africa and the global model EGM2008. The
comparison is limited to the maximum degree Nmax = 240. The solutions are based on the GOCE
data and obtained using four different regularization methods: the variance component estimation
proposed PSC method (bottom-right)
109
Figure 6.18: The differences between regional solutions in Central Africa and the global model GOCO03s. The
comparison is limited to the maximum degree Nmax = 240. The solutions are based on GOCE
110
6 Numerical results
The quality of the EGM2008 beyond the resolution of the GRACE-only models (say above n = 100) is
highly dependent on the available terrestrial data. In Central Africa with poor availability of terrestrial data
the EGM2008 cannot provide as good results as the GOCE data can. Therefore the deviations between the
regional solutions with the GOCE data and the EGM2008 are expected. The smaller differences between
regional solutions and the global model GOCO03s (a GRACE-GOCE combined model) indicate this explicitly.
Figures 6.17 and 6.18 illustrate the differences between regional solutions and the global models EGM2008
and GOCO03s respectively.
The differences between the regional solutions and the model GOCO03s are due to the fact that the regional
solutions are based on the GOCE data of only two months. In addition, only the Vzz components were used. In
contrast, the GOCO03s model is based on the combination of 7 years of GRACE KBR measurements as well
as 18 months of GOCE gravity gradiometry. In addition, 8 years of CHAMP orbit data and 5 years of SLR data
are also involved in the determination of this model. A fair comparison would be possible if the same data sets
were used to obtain the regional solution using SRBF.
Figure 6.19: Left: the dimensionless estimated coefficients using the PSC method on the Reuter grid points in
Central Africa. Right: the geoid heights synthesized using GOCO03s from degree n = 30 up to
degree n = 250 on the points of the Reuter grid. The coefficients reveal the shape of the geoid in
the corresponding frequency band.
Finally, figure 6.19 shows the value of the estimated coefficients using the PSC method on the Reuter grid
points. In addition, the synthesized geoid heights are given on the same locations. The synthesis is done using
the global model GOCO03s between spherical harmonic degrees 30 and 250. As it can be seen the general
shape of the geoid heights is shown by the coefficients which is an indication for the quality of the solution.
111
Regional solutions in Scandinavia
The description of the setup for regional gravity field recovery in Scandinavia is given in table 6.10. The total
number of gravity gradients (Vzz ) is about 29000 inside the data zone. With the total number of almost 2880
unknown parameters, the size of the design matrix is about 29000 × 2880.
Model specification
Remarks
◦
◦
◦
◦
the model zone: 50 ≤ φ ≤ 75 , 0 ≤ λ ≤ 50
Geographical limits
the data zone: 47 ≤ φ ≤ 78 , − 3 ≤ λ ≤ 53
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: 44 ≤ φ ≤ 81 , − 6 ≤ λ ≤ 56
observation type: Vz z at orbit altitude
Observations
The base functions
size: 2880 × 2880
The normal matrix N
using (5.77): γ 2 = 1.7 × 1022
using (5.88): γ 2 = 1.3 × 1021
Table 6.10: Specifications of the regional modelling in Scandinavia.
The condition number of the normal matrix is around 2 × 1019 revealing the strong ill-posedness of the regional
model. Table 6.11 summarizes the characteristics of the solutions.
γ2
orbit RMS
(Etvs)
surface RMS
(EGM2008, cm)
surface RMS
(GOCO03s, cm)
correlation of
VCE
7.316 × 1022
2.4 × 10−12
21.2
21.1
92.7%
GCV
8.638 × 1023
2.5 × 10−12
14.9
14.7
98.4%
L-curve
8.248 × 1023
2.5 × 10−12
15.0
14.8
98.4%
1024
10−12
11.3
11.3
98.8%
Regularization
method
PSC
7.578 ×
2.7 ×
Table 6.11: Summary of the regional solutions in Scandinavia and their quality measures. The solutions are
obtained using the Reuter grid. The RMS values on the Earth’s surface are obtained with respect to
the two global models; EGM2008 and GOCO03s.
112
6 Numerical results
Figure 6.20: The differences between regional solutions in Scandinavia and the global model EGM2008. The
proposed PSC method (bottom-right).
113
Figure 6.21: The differences between regional solutions in Scandinavia and the global model GOCO03s. The
114
6 Numerical results
According to the results given in table 6.11, the PSC method gives again the most promising results compared
to other approaches for the choice of regularization parameter. The L-curve and the GCV result in more or
less the same RMS values on the Earth’s surface. The VCE provides an insufficient amount of regularization
leading to the largest RMS value on the Earth’s surface.
The interesting fact in the case of Scandinavia is that the differences with respect to both EGM2008 and
GOCO03s models, are almost the same for each regularization approach. The reason is the availability of
enough terrestrial gravity observation used to determine the EGM2008 model. Therefore, the high frequencies
of the EGM2008 (regional spatial structures) are well determined and can be therefore compared to those
models obtained based on GOCE precise observations. Figures 6.20 and 6.21 display the differences between
the regionally derived geoids and the two global models EGM2008 and GOCO03s, respectively.
Scandinavia. Right: the geoid heights synthesized using GOCO03s from degree n = 30 up to
degree n = 250 on the points of the Reuter grid. The coefficients reveal the shape of the geoid in
the corresponding frequency band.
Figure 6.22 shows the value of the estimated coefficients using the PSC method on the Reuter grid points. The
synthesized geoid heights are given on the same locations in Scandinavia. In the synthesis, the coefficients of
the global model GOCO03s above the spherical harmonic degrees 30 have been used. As it can be seen, the
general shape of the geoid heights is shown by the coefficients which is an indication for the quality of the
solution.
115
Regional solutions in South America along the Andes
As the last test region, the regional gravity field modelling will be considered in South America in the area of
the Andes. The description of the model setup is given in table 6.12.
Model specification
Remarks
◦
◦
◦
◦
the model zone: −45 ≤ φ ≤ 15 , − 85 ≤ λ ≤ −60
Geographical limits
the data zone: −48 ≤ φ ≤ 18 , − 88 ≤ λ ≤ −57
◦
◦
◦
◦
◦
◦
◦
◦
the grid zone: −51 ≤ φ ≤ 21 , − 91 ≤ λ ≤ −54
observation type: Vz z at orbit altitude
Observations
The base functions
size: 6743 × 6743
The normal matrix N
using (5.77): γ 2 = 2.4 × 1021
using (5.88): γ 2 = 3.3 × 1020
Table 6.12: Specifications of the regional modelling in the area of the Andes.
The condition number of the normal matrix is around 1 × 1020 showing the strong ill-posedness of the regional
model. The solutions are obtained using four regularization methods and table 6.13 summarizes the characteristics
of the solutions.
γ2
orbit RMS
(Etvs)
surface RMS
(EGM2008, cm)
surface RMS
(GOCO03s, cm)
correlation of
VCE
2.015 × 1022
2.4 × 10−12
54.0
45.9
95.3%
GCV
2.850 × 1023
2.5 × 10−12
42.3
29.2
98.6%
L-curve
9.847 × 1022
2.5 × 10−12
47.1
37.0
98.1%
1023
10−12
Regularization
method
PSC
5.969 ×
2.6 ×
41.0
25.9
98.6%
Table 6.13: Summary of the regional solutions in the area of Andes and their quality measures. The solutions
are obtained using the Reuter grid. The RMS values on the Earth’s surface are obtained with respect
to the two global models; EGM2008 and GOCO03s
Again, the best results are obtained using the PSC method with the least RMS values on the Earth’s surface.
The GCV also provides rather satisfactory results with a slightly bigger RMS values than the PSC. The L-curve
analysis and the VCE methods are at the 3rd and 4th places among the methods.
116
6 Numerical results
The RMS values with respect to the EGM2008 are again larger compared to GOCO03s model. The reason is
the same as explained in the case of Central Africa. Figures 6.23 and 6.24 show the geoid differences between
the regional solutions and the models EGM2008 and GOCO03s in terms of geoid heights.
Figure 6.23: The differences between regional solutions in the area of the Andes and the global model
EGM2008. The comparison is limited to the maximum degree Nmax = 240. The solutions
are based on GOCE data and obtained using four different regularization methods. From left to
right: the variance component estimation, the generalized cross validation, the L-curve analysis
and the proposed PSC method.
Figure 6.24: The differences between regional solutions in the area of the Andes and the global model
GOCO03s. The comparison is limited to the maximum degree Nmax = 240. The solutions
are based on GOCE data and obtained using four different regularization methods. From left to
right: the variance component estimation, the generalized cross validation, the L-curve analysis
and the proposed PSC method.
117
the area of Andes. Right: the geoid heights synthesized using GOCO03s from degree n = 30 up
to degree n = 250 on the points of the Reuter grid. The coefficients reveal the shape of the geoid
in the corresponding frequency band.
Similar to the other two test regions, the values of the estimated coefficients using the PSC method on the Reuter
grid points is shown in Figure 6.25. The synthesized geoid heights on the same locations are also given in this
figure. The general shape of the geoid heights is can be illustrated by the coefficients which is an indication for
the quality of the solution.
6.3.4 Summary of regional solutions based on real GOCE data
In this section, the regional gravity field modelling was considered using SRBF based on the GOCE gravity
gradients. Two months of GOCE gravity gradients were used with a sampling rate of 1 second. The data
are down sampled to 5 seconds using a moving average filter. Only the Vzz component is used and other
components of the gravity tensor are not considered. The long wavelengths of the Vzz up to degree n = 30
are synthesized using the global model GOCO03s and subtracted from the observations. The Shannon kernel
with Nmax = 300 is employed as the base function distributed on the points of the Reuter grid corresponding
to Nmax = 300.
The regional solutions are determined in three test regions Central Africa, Scandinavia and the area of the
Andes. Four different parameter choice methods for the regularization parameter were applied to investigate
their performance in the regional inversion. These methods are: the variance component estimation (VCE),
the generalized cross validation (GCV), the L-curve analysis and our proposed parameter-signal correlation
(PSC). The solutions were compared then to the two global models EGM2008 and GOCO03s. The results of
the regional modelling are summarized as follows:
• At orbit level, all methods for the choice of regularization parameter lead to the same results. The RMS
values of the post-fit residuals along the orbit are the same. When the solutions are to be compared on the
Earth’s surface, the results are very different. Among the four methods for the choice of regularization
parameters, the proposed PSC method provides the best results with the least RMS values on the Earth’s
surface. The GCV, The L-curve analysis and the VCE methods provide larger RMS values on ground
level.
• The surface RMS values for different regularization methods are smaller in Scandinavia compared to
the other two regions. According to figure 6.21, the RMS value for the PSC and VCE methods are 11
118
6 Numerical results
and 21 cm respectively. The reason is the redundancy of observations which is rather big in this region
compared to the others.
• The geoid differences with respect to the global model EGM2008 are rather big in South America and
Central Africa. When the solutions are compared to the global model GOCO03s, the differences are
fairly smaller than EGM2008. This shows that our regionally derived geoids are noticeably better than
the EGM2008 (as a pre-GOCE model) in those regions with insufficient available terrestrial data. This
improvement is not seen in regions like Scandinavia where the coverage of terrestrial gravity data is
rather good.
• The differences between our regional solutions and the geoid from the model GOCO03s are due to the
fact that GOCO03s is a combined gravity field model. GOCO03s is based on several years of the GRACE
and nearly one year of the GOCE observations. On the other hand, our regional solutions are based on
only two months of the GOCE Vzz observations. Nevertheless, the differences are in the range of current
accumulated geoid errors (c.f. figure 2.5) which indicates the success of regional gravity field modelling
as well as our proposed regularization method.
119
We investigated the regional gravity field modelling based on satellite observations. The base functions used
for the regional gravity field modelling are band-limited SRBF. The objective was to develop a simple and
clear guideline for the regional gravity field modelling based on satellite data. The investigations were carried
out using simulated data of a GRACE-like mission as well as the real GOCE observations.
The spherical harmonics and SRBF were compared, first, on the global scale. It was numerically shown that
these two base functions span the same function space and result in the same accuracy for the representation
of the global gravity field. In addition, we showed that the spatial pattern of the scaling coefficients associated
with the SRBF are highly correlated with the gravitational potential difference or geoid heights. This is
due to the space-localizing property of the SRBF. This high correlation is considered as a prior information
about the unknown scaling coefficients in regional gravity field modelling. Such valuable prior information
gave an insight into the proper regularization of regional gravity modelling and led to the development of the
parameter-signal-correlation (PSC) method.
Model setup using SRBF
The regional gravity field modelling was studied in detail from different perspectives. First, the mathematical
explanation of regional modelling using SRBF and its connection to the global modelling were given. The
truncation of the data and base functions which cause severe instabilities in the inversion step were explained
where we partitioned the global observation equations to sub-regions. We showed how the observation equation
for the regional gravity field modelling is extracted from the global observation and discussed the contribution
of the missing components.
The procedure of model setup for regional gravity field modelling was considered in detail. The crux of the
regional gravity field modelling using SRBF is the variety of different choices for model setup as well as the
inversion process. We divided these choices into seven groups and discussed each specifically. These choices
are the shape of the SRBF, the maximum degree of expansion, the removal of the long wavelengths, the position
of the SRBF, the size of the data zone, the size of the grid zone and finally the inversion process. According to
our investigations and numerical results given in chapter 6, the following concluding remarks can be made for
these choices.
1. Shape of the SRBF: We classified the band-limited SRBF into smoothing and non-smoothing base
functions. Examples for the smoothing SRBF are CuP, Blackman and Spline kernels which include
built-in low-pass filters. The Shannon kernel (as a special case of the point mass kernel) belongs to
the class of non-smoothing SRBF if Nmax is chosen sufficiently beyond the expected frequency content
of the signal. As a result of using smoothing kernels, the severe observation’s noise in high frequency
components of the signal will be considerably reduced. On the other hand, the use of smoothing SRBF
causes the filtering of high-frequency parts of the signal as well. Increasing the bandwidth of these
functions by choosing a larger Nmax to cover the expected spectrum of the signal imposes much more
base functions to the model which is unnecessary. Therefore, we confined our investigations to the
Shannon kernel as a non-smoothing kernel. This kernel leaves the observations unchanged. Therefore,
for the satellite data, the use of the SRBF with Shannon kernel is recommended provided that the solution
is obtained by means of a proper regularization method.
2. Maximum degree of the expansion: the maximum degree of the expansion, Nmax is directly dependent
on the expected frequency content of the signal. For instance, Nmax for the GRACE monthly solutions
and the GOCE observations are nominally 120 and 250, respectively. We recommend to set this number
120
slightly bigger than these values so that it is guaranteed that the signal is not undesirably filtered. We
chose 130 and 300 as the maximum degree of the expansion for GRACE and GOCE observations which
are beyond the expected resolution of the GRACE monthly solutions and the the GOCE static field.
3. Removal of the long wavelengths: Since it is not possible to model the long wavelengths of the gravity
field on regional scales, these parts must be excluded from the observations. The extent to which the
long wavelengths are removed is dependent on the size of the region. The smaller the region is the
more removal is needed. In our computations, we synthesized and subtracted the long wavelengths up to
degree n = 30. This number was obtained using a rule of thumb based on the size of the target region.
Our investigations show that the removal of long wavelengths more than necessary does not improve the
accuracy of the regional solutions considerably.
4. Position of the SRBF: There are several kinds of grids which can be used to define the location of base
functions. Using different kinds of grids does not change the quality of the solutions provided that the
grid offers a homogeneous point distribution. The slight differences between various grids can be refined
by means of regularization in the inversion step. Examples of homogeneous point distribution are the
Reuter grid and the Fibonacci grid which can be alternatively used with no preference.
5. Size of the data zone: To obtain a useful regional solution, the size of the data zone must be larger than
the size of the model zone, where the representation is desired. The extension of the data zone depends
on the type of observations and the frequency content of the reduced signal. We related the size of the
data zone to the frequency content of the reduced signal and the satellite altitude and proposed a rule
of thumb given by equations (4.16) and (4.17) to compute the minimum required extension. More data
extension seems to be unnecessary since no significant improvement is achieved.
6. Size of the grid zone: The base functions which are outside, but close to the borders of the data zone
can still have significant contribution to the solution. Thus the grid zone should be still larger than the
data zone. We also proposed a rough rule to determine the extension of the grid zone. This estimation is
dependent on the bandwidth of the the SRBF which is connected to the maximum degree of expansion
Nmax .
7. Inversion process: The modelling of the regional gravity field using SRBF is strongly ill-posed even
though the above 6 choices are made reasonably. The reason is the regional confinement of the data
as well as the base functions which are, in principle, globally defined. Thus, additional information is
required to provide sufficient regularity for the solution. A useful solution must be achieved only by
means of a proper regularization method.
Inversion and regularization
The Tikhonov regularization as a successful regularization method for many inverse problems gives sufficient
regularity provided that the regularization parameter is chosen correctly. There are several well-known parameter
choice methods which can be used for Tikhonov regularization. The variance component estimation (VCE),
the generalized cross validation (GCV) and the L-curve analysis are examples of such methods. Nevertheless,
the use of existing methods for the choice of regularization parameter cannot solely regularize the regional
solutions. If these methods are used, other measures of regularity (such as using smoothing SRBF) should
be incorporated in the model setup. An important achievement of this research study is the development of
a new method for the choice of the regularization parameter which provides adequate regularization for the
regional inversions. The proposed parameter-signal correlation (PSC) method is a new approach to choose the
right (Tikhonov) regularization parameter. The method works based on the fact, that the scaling coefficients
αk represent the geometry of the residual gravitational potential or geoid heights. Thus, the desired unknown
coefficients αk should be highly correlated to the target residual potential on the Earth’s surface.
The regularization parameter is a number between the smallest and the largest singular values of the ill-posed
normal matrix. Since it is a vast range of numbers (over 18 orders of magnitude for regional gravity field
solutions), having an initial guess for the regularization parameter is very essential for reducing the computational
121
burden. Two methods were also proposed to obtain a realistic guess for the regularization parameter which
result in more or less the same numbers. Using these initial values, the final regularization parameter can be
rapidly found using the PSC method. The proposed methods for the initial regularization parameter is not
restricted to the PSC method and can be used with other parameter choice methods to reduce the computational
costs.
Summary of the numerical results
The performance of the proposed PSC method was assessed in comparison with VCE, GCV and the L-curve
methods. To compare the methods reasonably, several regional solutions were determined in different test
areas. In addition, the solutions are obtained, separately, based on simulated GRACE data and real the GOCE
observations. The following conclusions can be made accordingly:
1 Based on the simulated GRACE data, a global solution using spherical harmonics and several regional
solutions using SRBF have been determined. As quality measure, the differences between solutions and
the input gravity field model have been computed and their RMS values were determined. The RMS
of the differences contain the total error (model error and the observation noise) and is a good measure
for the quality assessment. The regional solutions obtained using VCE, GCV and L-curve analysis have
larger RMS values compared to the global spherical harmonics. On the contrary, the PSC method gives
equivalent results to the spherical harmonic solutions in high-latitude regions and better results with less
RMS values in equatorial areas. The GRACE north-south stripes seen in GRACE monthly solutions are
remarkably reduced in regional solutions using the PSC regularization method.
2 Among VCE, GCV, L-curve and the PSC methods, the PSC gives the most promising results with less
RMS values. The L-curve also provides satisfactory results with slightly larger RMS values compared to
the PSC. The other two methods, i.e. VCE and GCV, cannot regularize the regional solutions sufficiently
and result in rather large geoid RMS. The use of the VCE and GCV methods (for regional gravity field
modelling) should be made with other kernels such as the Blackman, CuP and Spline which have built-in
regularity defined by their Legendre coefficients bn . This fact has not been addressed in previous studies.
The advantage of the PSC method is that it provides adequate regularization so that the base
functions remain simple with no further efforts to define the Legendre coefficients bn .
3 To assess the regional solutions based on other data sets, we also employed two months of GOCE
gravity gradients (Vzz ). Three regional solutions were determined in South America along the Andes, in
Central Africa and in Scandinavia. They were compared to the high-resolution global gravity field model
EGM2008 and the recent satellite based global model GOCO03s. The EGM2008 is chosen because it is
a pre-GOCE gravity field model and can show the improvements achieved by GOCE data. The reason
for choosing the GOCO03s is that this model is a combined model based on the GRACE and GOCE data
and can be considered as the state-of-the-art gravity field model.
Again, the PSC method gives the least geoid RMS compared to the other methods. This is another
indication for the success of the PSC regularization method. Moreover, the results reveal that in the
area of Andes as well as the Central Africa, regional solutions are considerably better than the global
model EGM2008. This is evident from figures 6.17 and 6.23. The reason is that in these areas, there
have not been enough terrestrial data to be incorporated in the determination of EGM2008. In contrast,
in Scandinavia where terrestrial data have been available, there is no significant difference between
EGM2008 and the solutions including GOCE observations. The improvement achieved for the quality
of regional solutions in comparison with the model EGM2008 does have two clear messages: first, even
two months of GOCE observations can improve the quality of the gravity field in medium and short
wavelengths compared to pre-GOCE models. Second, the regional gravity field modelling using the
SRBF provide promising results and can compete (and outperforms) the global models.
4 The differences between our regional solutions and the global model GOCO03s can be seen from different
perspectives. First, the differences are almost in the range of accumulated geoid errors shown in figure
122
2.6 which shows the accumulated geoid errors of some recent global models. This is more evident for
the case of the regional solution in Scandinavia where a better solution is obtained according to the
dense GOCE orbit tracks. Secondly, it should be noted that the regional solutions are obtained based
on two months of GOCE data only which in addition, were limited to the Vzz components. Finally, the
GOCO03s is a combined model based on the data from several satellite missions. A fair comparison
would be possible if the regional solutions were also obtained based on the same data sets. Incorporating
more GOCE observations as well as combination with other satellite data will increase the accuracy of
regional solutions considerably and is left for further works.
Further works
1. The proposed PSC method gives an insight into a data-adaptive choice for the regularization parameter.
It requires a prior gravity field model. The prior gravity field model does not have to be a state-of-the-art
model and an approximate model also suffices for the PSC method. Nevertheless, it is desired to get
the PSC method working even without the need for an input gravity field model. The method can be
modified by means of iteration so that no prior gravity field model might be needed.
2. The stochastic relations of the satellite observations can also help to provide prior information about
the variance and covariance of the desired solution. In particular one can try to describe the stochastic
effects of the observations outside the data zone on the final solution. This should be taken into account
in connection with the equations (4.1), (4.2) and (4.3) which describe the deterministic effects of the
observations outside the target region.
3. Incorporating other components of GOCE gravity gradient tensor will improve the quality of the regional
solutions. This is not only due to the use of much more observations, but also due to the fact that other
components such as Vxx and Vxy are more accurate than the Vzz and contain additional information about
the features of the Earth’s gravity field. This is to be done in further regional gravity field modelling with
the PSC method.
4. For regional gravity field determination based on the GRACE (and the GRACE follow-on) mission, it is
recommended to use the modified acceleration approach proposed at the technical University of Delft or
the integral equation approach (c.f. section 2.2). The advantage of these methods for regional gravity field
modelling is the reduced observation noise according to their observation equations. As we discussed
in section 5.8, less observation noise requires less regularization in regional gravity field modelling and
leads to better solutions.
5. Finally, the PSC method shall be adopted for data combination in regional gravity determination. An
idea is to combine the PSC, as a regularization parameter choice method, and the VCE as a weighting
approach for different data sets. This could be a possible subject for further works.
Bibliography
123
Bibliography
Alberts, B. (2009). Regional gravity field modeling using airborne gravimetry data. Publications on geodesy
70, Technical University of Delft. ISBN: 978 90 6132 312 9.
Amiri-Simkooei, A. (2007). Least-Squares Variance Component Estimation, Theory and GPS Applications.
Publications on geodesy 64, Technical University of Delft. ISBN: 978 90 6132 301 3.
Antoni, M. (2012). Nichtlineare Optimierung regionaler Gravitationsfeldmodelle aus SST-Daten. PhD thesis,
Institute of Geodesy, University of Stuttgart. ISBN 978-3-7696-5082-2.
Austen, G. and Grafarend, E. (2004). Gravitational field recovery from GRACE data of type high-low and
low-low SST. In The conference proceedings of the Joint CHAMP/GRACE Science Meeting, Potsdam,
Germany.
Bentel, K., Schmidt, M., and Gerlach, C. (2013). Different Radial Basis Functions and their Applicability for
Regional Gravity Field Representation on the Sphere. GEM - International Journal on Geomathematics, 4,
Pages 67–96.
Beutler, G., Jäggi, A., Mervart, L., and Meyer, U. (2010). The celestial mechanics approach: theoretical
foundations. Journal of Geodesy, 84, Pages 605–624.
Biancale, R., Balmino, G., Lemoine, J., Marty, J., Moynot, B., Barlier, F., Exertier, P., Laurain, O., Gegout,
P., Schwintzer, P., Reigber, C., Bode, A., König, R., Massmann, F., Raimondo, J., Schmidt, R., and Zhu, S.
(2000). A new global Earth’s gravity field model from satellite orbit perturbations: GRIM5-S1. Geophysical
Research Letters, 27, Pages 3611–3614.
Bisnath, S. (2004). Precise orbit determination of low Earth orbiters with a single GPS receiver based,
geometric strategy. Technical Report, Department of Geodesy and Geomatics Engineering, University of
New Brunswick.
Bjerhammer, E. (1975). Discrete approaches to the solution of boundary value problem in phyiscal geodesy.
Bollettino Di Geodesia E Scienze Affini, 34.
Bjerhammer, E. (1985). On a relativistic geodesy. Bollettino Di Geodesia E Scienze Affini, 59, Pages 207–220.
Bosch, W. (2002). Geodetic Applications of Satellite Altimetry, a review. IAG Workshop on Satellite Altimetry,
Wuhan, 08-13 September. http://space.cv.nctu.edu.tw/altimetryworkshop/Lecture/keynote-bosch.pdf.
Bouman, J. (2000). Quality assessment of satellite-based global gravity field models. Publications on geodesy
48, Technical University of Delft. ISBN 9061322707.
Bouman, J. (2007). Alternative method for rotation to TRF. The European GOCE Gravity Consortium, 1
Edition. GO-TN-HPF-GS-0193.
Bouman, J., Fiorot, S., Martin, F., Gruber, T., Schrama, E., Tscherning, C., Veicherts, M., and Visser, P. (2011).
GOCE gravitational gradients along the orbit. Journal of Geodesy, 85, Pages 791–805.
Brieden, P. and Müller, J. (2011). Current results of GOCE in-orbit validation via the cross-over approach. In
L. Ouwehand (Ed.), Proceedings of 4th International GOCE User Workshop. European Space Agency.
Calvetti, D., Golub, G., and Reichel, L. (1999). Estimation of the L-curve via Lanczos bidiagonalization. BIT
Numerical Mathematics, 39, Pages 603–619.
124
Bibliography
Calvetti, D., Hansen, P., and Reichel, L. (2002). L-curve curvature bounds via Lanczos bidiagonalization.
Electronic Transactions on Numerical Analysis, 14, Pages 20–35.
Calvetti, D., Reichel, L., and Shuibi, A. (2004). L-curve and curvature bounds for Tikhonov regularization.
Numerical Algorithms, 35, Pages 301–314.
Case, K., Kruizinga, G., and Wu, S. (2010). GRACE Level 1B Data Product User Handbook. Jet Propulsion
Laboratory California Institute of Technology JPL. D-22027.
Cheney, W. and Kincaid, D. (2008). Numerical Mathematics and computing, sixth edition. Brooks/Cole
Publishing Company. ISBN-13: 978-0-495-11475-8.
Chung, J., Nagy, J., and OLeary, D. (2008). A weighted-GCV method for Lanczos-Hybrid regularization.
Electronic Transactions on Numerical Analysis, 28, Pages 149–167.
Colombo, O. (1981). Numerical methods for harmonic analysis on the sphere. Technical Report 310,
Department of Geodetic Science and Surveying, The Ohio State University, Columbus, Ohio. 139pp.
Dempster, A., Schatzoff, M., and Wermuth, N. (1977). A simulation study of alternatives to ordinary
least-squares. Journal of the American Statistical Association, 72, Pages 77–106.
Ditmar, P. and Klees, R. (2002). A method to compute the Earth’s gravity field from SGG/SST data to be
acquired by GOCE satellite. Delft University press.
Edmonds, A. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN:
9780691025896.
Eicker, A. (2008). Gravity Field Refinement by Radial Base Functions from In-situ Satellite Data. PhD thesis,
Institute of geodesy and geo-information, University of Bonn. ISBN 978-3-7696-5088-4.
Eicker, A., Mayer-Gürr, T., Ilk, K., and Kurtenbach, E. (2010). Regionally refined gravity field models from
in-situ satellite data. In F. Flechtner, T. Gruber, A. Güntner, M. Mandea, M. Rothacher, T.Schöne, and
J. Wickert (Ed.), System Earth via Geodetic-Geophysical Space Technologies, Pages 255–264. Springer.
Fengler, M., Freeden, W., and Kusche, J. (2005). Multiscale geopotential solutions from CHAMP orbits and
accelerometry. In C. Reigber, H. Lühr, P. Schwintzer, and J. Wickert (Ed.), Earth observation with CHAMP,
results from three years in orbit., Pages 139–144. Springer.
Flury, J. and Rummel, R. (2005). Future satellite gravimetry and earth dynamics. Springer, Dordrecht, The
Netherlands.
Freeden, W. (1999). Multiscale modelling of spcaeborne geodata. Teubner, Stuttgart.
Freeden, W., Gervens, T., and Schreiner, M. (1998). Constructive approximation on the sphere (with
applications to geomathematics). Clarendon Press, Oxford.
Gerlach, C., Földvary, L., Svehla, D., Gruber, T., Wermuth, M., Sneeuw, N., Frommknecht, B., Oberndorfer,
H., Peters, T., Rothacher, M., Rummel, R., and Steigenberger, P. (2003). A CHAMP-only gravity field model
from kinematic orbits using the energy integral. Geophysical Research Letters, 30, Page 2037.
GFZ (2013). ICGEM - Table of Global Gravity Field Models. http://icgem.gfz-potsdam.de/
ICGEM/ICGEM.html.
Gloub, G. and van Loan, C. (1996). Matrix computations, third edition. John Hopkins University Press,
Baltimore, MD.
Golub, G., Heath, M., and Vahba, G. (1979). Generalized Cross-Validation as a method for choosing a Good
Ridge parameter. Technometrics, 21, Pages 215–223.
Bibliography
125
Gonzalez, A. (2010). Measurement of areas on a sphere using Fibonacci and latitude-longitude lattices.
Mathematical Geosciences, 42, Pages 49–64.
Grafarend, E. and Vanicek, P. (1980). On the Weight Estimation in Leveling. Technical Report, NOAA
Technical Report NOS 86, NGS 17.
Gruber, T. (2004). Validation concepts for gravity field models from new satellite missions. In H. Lacoste
(Ed.), Proceedings of the 2nd International GOCE User Workshop: GOCE, The Geoid and Oceanography,
ESA SP-569. ESA.
Gruber, T. (2009). Evaluation of EGM2008 gravity field by means of GPS-levelling and sea surface topography
solutions. Newton’s Bulletin, Bureau Gravimetrique International (BGI), 4, Pages 3–17.
Gruber, T., Brockmann, J., Schuh, W., and l. Krasbutter (2010). GOCE Level 2 Product Data Handbook. The
European GOCE Gravity Consortium EGG-C, issue 4, revision 3 Edition.
Gruber, T., Visser, P., and Ackermann, C. (2011). Validation of GOCE gravity field models by means of orbit
residuals and geoid comparisons. Journal of Geodesy, 85, Pages 845–860.
Hadamard, J. (1923). Lectures on the Cauchy Problem in Linear Partial Differential Equations. Yale University
Press, Haven.
Han, S., Jekeli, C., and Shum, C. (2002). Efficient Gravity Field Recovery Using in situ Disturbing Potential
Observables from CHAMP. Geophysical Research Letters, 29, Pages 36/1–36/4.
Han, S., Jekeli, C., and Shum, C. (2003). Static and temporal gravity field recovery using GRACE potential
difference observables. Advances in Geosciences, 1, Pages 19–26.
Han, S., Shum, C., Jekeli, C., and Alsdorf, D. (2005). Improved estimation of terrestrial water storage changes
from GRACE. Geophysical Research Letters, 32, Page L07302.
Han, S., Shum, C., and Jekeli, C. (2006). Precise estimation of in situ geopotential difference from GRACE
low-low satellite-tosatellite tracking and accelerometry data. Journal of Geophysical Research, 111, Page
B04411.
Hansen, P. (1990a). The discrete picard condition for discrete ill-posed problems. BIT Numerical Mathematics,
30, Issue 4, Pages 658–672.
Hansen, P. (1990b). Truncated singular value decomposition solutions to discrete ill-posed problems with
ill-determined numerical rank. SIAM Journal on Scientific and Statistical Computing, 11, Pages 503–518.
Hansen, P. (1997). Rank Deficient and Discrete Ill-Posed Problems. SIAM, Philadelphia.
Hansen, P. (2000). The L-Curve and its Use in the Numerical Treatment of Inverse Problems. In
in Computational Inverse Problems in Electrocardiology, ed. P. Johnston, Advances in Computational
Bioengineering, Pages 119–142. WIT Press.
Hansen, P. (2010). Discrete Inverse Problems, Insight and Algorithms. SIAM, Philadelphia.
Hansen, P. and OLeary, D. (1993). The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems.
SIAM Journal on Scientific Computing, 14, Pages 1487–1503.
Hashemi, F., Ditmar, P., Klees, R., Liu, X., Zhao, Q., and Guo, J. (2012). The Earth’s static gravity field model
DGM-1S from an optimal combination of GRACE and GOCE data: computation and validation aspects.
Journal of Geodesy, in review.
Heiskanen, W. and Moritz, H. (1967). Physical geodesy. Freeman, San Francisco.
126
Bibliography
Higham, N. (1987). A Survey of condition number estimation for triangular matrices. Society for Industrial
and Applied Mathematics, 29, Pages 575–596.
Hirt, C., Bürki, B., Somieski, A., and Seeber, G. (2010). Modern Determination of vertical deflections using
digital zenith cameras. Journal Surveying Engineering, 136, Pages 1–12.
Hofmann, B. and Moritz, H. (2005). Physical Geodesy. SpringerWienNewYork.
Hutchinson, M. (1990). A stochastic estimator of the trace of the influence matrix for laplacian smoothing
splines. Communications in Statistics, Simulation and Computation, 19, Pages 433–450.
Ihde, J., Wilmes, H., Müller, J., Denker, H., Voigt, C., and Hosse, M. (2010). Validation of Satellite Gravity
Field Models by Regional Terrestrial Data Sets. In F. Flechtner, T. Gruber, A. Güntner, M. Mandea,
M. Rothacher, T. Schöne, and J. Wickert (Ed.), System Earth via Geodetic-Geophysical Space Techniques,
Advanced Technologies in Earth Sciences, Pages 227–296. Springer.
Ilk, K. (1993). Regularization for high resolution gravity field recovery by future satellite techniques. In
G. Anger, R. Gorenflo, H. Jochmann, H. Moritz, and W. Webers (Ed.), Inverse problems: principles and
applications in geophysics, technology, and medicine. AkademieVerlag, Berlin.
Jekeli, C. (1999). The determination of gravitational potential differences from satellite-to-satellite tracking.
Celestial Mechanics and Dynamical Astronomy, 75, Pages 85–101.
Jekeli, C. (2005). Spline representation of functions on a sphere for geopotential modeling. Technical Report
475, Department of Geodetic Science, The Ohio State University.
Jäggi, A., Hugentobler, U., Bock, H., and Beutler, G. (2007). Precise orbit determination for GRACE using
undifferenced or doubly differenced GPS data. Advances in Space Research, 39, Pages 1612–1619.
Kang, Z., Tapley, B., Bettadpur, S., Ries, J., Nagel, O., and Pastor, R. (2006). Precise orbit determination for
the GRACE mission using only GPS data. Journal of Geodesy, 80, Pages 322–331.
Kaula, W. (1966). Theory of Satellite Geodesy, Applications of Satellites to Geodesy. Dover Publications, INC.
Mineola, New York.
Keller, W. (2004). Wavelets in Geodesy and Geodynamics. Walter de Gruyter. Berlin. New York.
Klees, R., Tenzer, R., Prutkin, I., and Wittwer, T. (2008). A data-driven approach to local gravity field modelling
using spherical radial basis functions. Journal of Geodesy, 82, Pages 457–471.
Knudsen, P. (1987). Estimation and Modelling of the Local Empirical Covariance Function Using Gravity and
Satellite Altimeter Data. The Journal of the international association of Geodesy, 61, N2, Pages 145–160.
Koch, K. (1999). Parameter Estimation and Hypothesis Testing in Linear Models. Springer-Verlag Berlin
Heidelberg NewYork.
Koch, K. and Kusche, J. (2002). Regularization of geopotential determination from satellite data by variance
components. Journal of Geodesy, 76, Pages 259–268.
Koop, R. (1993). Gloabal gravity field modelling using satellite gravity gradiometry. PhD thesis, Technical
University of Delft.
Kreyszig, E. (1978). Introductory Functional Analysis with Applications. John Wiley & Sons, USA.
Kroes, R. (2006). Precise relative positioning of formation flying spacecraft using GPS. PhD thesis, Technical
Kusche, J. (2003). Noise variance estimation and optimal weight determination for GOCE gravity recovery.
Advances in Geosciences, 1, Pages 81–85.
Bibliography
127
Kusche, J. and Klees, R. (2002). Regularization of gravitay field estimation from satellite gravity gradients.
Journal of Geodesy, 76, Pages 359–368.
Kusche, J. and van Loon, J. (2005). Statistical Assessment of CHAMP Data and Models Using the Energy
Balance Approach. In C. Reigber, H. Lühr, P.Schwintzer, and J. Wickert (Ed.), Earth Observation with
CHAMP, Results from Three Years in Orbit. Springer.
Lawless, J. and Wang, P. (1976). A simulation study of ridge and other regression estimators. Communications
in Statistics - Theory and Methods, A5, Pages 307–323.
Lee-Lueng, F. and Cazenave, A. (2000). Satellite Altimetery and Earth Sciences - A Handbook of Techniques
and Applications. International Geophysics series.
Lemoine, F., Luthcke, S., Rowlands, D., Chinn, D., Klosko, M., and Cox, C. (2007). The use of mascons
to resolve time-variable gravity from GRACE, Volume 130, Pages 231–236. International Association of
Geodesy Symposia.
Lio, X. (2008). Global gravity field recovery from satellite-to-satellite tracking data with acceleration
approach. PhD thesis, Technical University of Delft.
MacLeod, A. (1988). Finite-dimensional regularizations with nonidentity smoothing matrices. Linear Algebra
and its Applications, 111, Pages 191–207.
Marchenko, A. (1998). Parametrization of the Earth’s gravity field:point and line singularities.
Astronomical and Geodetic Society, Lviv, Ukraine.
Lviv
Marchenko, A. (2003). Regional gravity field model from satellite altimetry, gravimetry and GPS-levelling data
in Black Sea area. Bollettino Di Geodesia E Scienze Affini, 1XII, Pages 245–259.
Marchenko, A., Barthelmes, F., Mayer, U., and Schweintzer, P. (2001). Regional geoid determination: an
application to airborne gravity data in the Skagerrak. Technical Report STR01/07, GeoForschungsZentrum,
Potsdam.
Martinsson, P.-G., Rokhlin, V., and Tygert, M. (2006). A randomized algorithm for the approximation of
matrices. Technical Report, Yale University Department of Computer Science.
Martinsson, P.-G., Rokhlinb, V., and Tygert, M. (2010). A randomized algorithm for the decomposition of
matrices. Applied and Computational Harmonic Analysis, 30, Pages 47–68.
Mayer-Gürr, T. (2006). Gravitationsfeldbestimmung aus der Analyse Kurzer Bahnbögen am Beispiel der
Satellitenmissionen CHAMP und GRACE. PhD thesis, University of Bonn.
Mayer-Gürr, T. (2012). The new combined satellite only model GOCO03s. International Symposium on
Gravity, Geoid and Height Systems, Venice (Poster).
Mayer-Gürr, T., Ilk, K., Eicker, A., and Feuchtinger, M. (2005). ITG-CHAMP01: a CHAMP gravity field model
from short kinematic arcs over a one-year observation period. Journal of Geodesy, 78, Pages 462–480.
Müller, C. (1966). Spherical harmonics, Lecture notes in mathematics, Volume 17. Springer Verlag, Berlin.
Mohammad-Karim, M. (1981). Diagramatic approach to solve least-squares adjustment and collocation
problems. Technical Report 83, Department of geodesy and geomatics engineering, University of New
Brunswick.
Montenbruck, O. and Gill, E. (2000). Satellite orbits: models, methods and aoolications. Springer Verlag,
Heidelberg.
Moritz, H. (1980). Advanced Physical Geodesy. Herbert Wichmann Verlag Karlsruhe, Abacus Press Tunbridge
Wells Kent.
128
Bibliography
Moritz, H. and Sünkel, H. (1978). Approximation methods in Geodesy. Herbert Wichmann Verlag Karlsruhe.
Neumann, J. (1968). Mathematische Grundlagen der Quantenmechanik. Grundlagen der Mathematuschen
Wissenschaften, Band 38, Springer-Verlag, Heidelberg.
Orfanidis, S. (1996). Optimum Signal Processing. An Introduction. Prentice-Hall, Englewood Cliffs, NJ.
Pail, R., Fecher, T., Murböck, M., Rexer, M., Stetter, M., Gruber, T., and Stummer, C. (2013). Impact of
GOCE Level 1b data reprocessing on GOCE-only and combined gravity field models. Studia Geophysica et
Geodaetica, 57, Pages 155–173.
Panet, I., Flury, J., Biancale, R., Gruber, T., Johannessen, J., den Broeke, M. V., Van-Dam, T., Gegout, P.,
Hughes, C., Ramillien, G., Sasgen, I., Seoane, L., and Thomas, M. (2012). Earth System Mass Transport
Mission (e.motion): A Concept for Future Earth Gravity Field Measurements from Space. Surveys in
Geophysics, 34, Pages 141–163.
Payne, M. (1971). Truncation effects in geopotential modelling. Analytical Mechanics Associates, Seabrook,
Maryland.
Petit, G. and Luzum, B. (2010). IERS Conventions 2010. International Earth Rotation and Reference Systems
Service. ADA535671.
Ramillien, G., Biancale, R., Gratton, S., Vasseur, X., and Bourgogne, S. (2011). GRACE-derived surface water
mass anomalies by energy integral approach: application to continental hydrology. Journal of Geodesy, 85,
Pages 313–328.
Reginska, T. (1996). A regularization parameter in discrete ill-posed problems. SIAM Journal on Scientific
Computing, 17, Pages 740–749.
Reigber, C. (1989). Gravity field recovery from satellite tracking data. In Sanso.F and Rummel.R (Ed.), Theory
of satellite geodesy and gravity fild determination, Volume 25, Pages 197–234. Springer.
Reubelt, T., Austen, G., and Grafarend, W. (2003). Harmonic analysis of the earht’s gravitational field by
means of semi-continuous ephemerides of a low Earth orbiting GPS-tracked satellite. Case study: CHAMP.
Reubelt, T., Götzelmann, M., and Grafarend, W. (2006). Harmonic analysis of the earht’s gravitational field
from kinematic CHAMP orbits based on numerically derived satellite accelerations. In J. Flury, R. Rummel,
C. Reigber, M. Rothacher, G. Boedecker, and U. Schreiber (Ed.), Observation of the Earth from space, Pages
27–42. Springer.
Reuter, R. (1982). Über Integralformeln der Einheitssphäre und harmonische Splinefunktionen. Technical
Report, Veröffentlichungen des Geodätischen Instituts der Rheinisch-Westfälischen Technischen Hochschule
Aachen.
Rummel, R. (1979).
Determination of short-wavelength components of the gravity field from
satellite-to-satellite tracking or satellite gradiometry. Manuscripta geodaetica, 4/2, Pages 107–148.
Rummel, R., Reigber, C., and Ilk, K. (1978). The use of satellite-to-satellite tracking for gravity parameter
recovery. In S. Heiber and T. Guyenne (Ed.), Proceedings of the European Workshop on Space
Oceanography, Navigation and Geodynamics (SONG), Pages 153–161. esa SP-137.
Rummel, R., Balmino, G., Johannessen, J., Visser, P., and Woodworth, P. (2002). Dedicated gravity field
missions-principles and aims. Journal of Geodynamics, 33, Pages 3–20.
Rummel, R., Gruber, T., Yi, W., and Albertella, A. (2012). GOCE: Its Principles and Science. In H. Schuh,
J. Böhm, T. Nilsson, and N. Capitaine (Ed.), Proceedings of the Journées 2011 "Systèmes de référence
spatio-temporels", Volume 2012. Vienna University of Technology.
Bibliography
129
Rust, B. (1998). Truncating the Singular Value Decomposition for Ill-Posed Problems. Technical Report
NISTIR 6131, Mathematical and Computational Sciences Division.
Save, H. (2009). Using regularization for error reduction in GRACE gravity estimation. PhD thesis, The
university of Texas at Austin.
Save, H. and Bettadpur, S. (2012). Reducing errors in the GRACE gravity solutions using regularization.
Scales, J. (1996). Uncertainties in seismic inverse calculations. In B. Jacobsen, K. Mosegaard, and P. Sibani
(Ed.), Inverse Methods, Volume 63, Lecture Notes in Earth Sciences, Pages 79–97. Springer Verlag, Berlin.
Schachtschneider, R., Holschneider, M., and Mandea, M. (2010). Error distribution in regional inversion of
potential field data. Geophsical Journal International, 181, Pages 1428–1440.
Schmidt, M., Han, S.-C., Kusche, J., Sanchez, L., and Shum, C. K. (2006). Regional high-resolution
spatiotemporal gravity modeling from GRACE data using spherical wavelets. Geophysical Research Letters,
33, Page L08403.
Schmidt, M., Fengler, M., Mayer-Gürr, T., Eicker, A., Kusche, J., Sanchez, L., and Han, S.-C. (2007). Regional
gravity field modeling in terms of spherical base functions. Journal of Geodesy, 81, Pages 17–38.
Schneider, M. (1968). A general method of orbit determination. Technical Report, Royal Aircraft Translation
no. 1279, Ministry of Technology, Farnborough, UK.
Sheard, B., Heinzel, G., Danzmann, K., Shaddock, D., Klipstein, W., and Folkner, W. (2012). Intersatellite
laser ranging instrument for the GRACE follow-on mission. Journal of Geodesy, 86, Pages 1083–1095.
Souza and César, R. (2010).
Kernel Functions for Machine Learning
http://crsouza.blogspot.com/2010/03/kernel-functions-for-machine-learning.html.
Applications.
Steven, W. (1997). The Scientist and Engineer’s Guide to Digital Signal Processing. California Technical
Publishing, San Diego, California.
Strang, G. and Borre, K. (1997). Linear Algebra, Geodesy, and GPS. Wellesley-Cambridge Press.
Stummer, C., Gruber, T., Bouman, J., and s. Rispens (2008). GOCE gradiometry - A Guide for users. IAG,
international symposium, Gravity, geoid and Earth observations. 23-27 June 2008, China.
Tapley, B., Bettadpur, S., Watkins, M., and Reigber, C. (2004). The gravity recovery and climate experiment:
Mission overview and early results. Geophysical Research Letters, 31, Page L09607.
Tapley, B., Ries, J., Bettadpur, S., Chambers, D., Cheng, M., Condi, F., Gunter, B., Kang, Z., Nagel, P., Pastor,
R., Pekker, T., Poole, S., and Wang, F. (2005). GGM02: An improved Earth gravity field model from
GRACE. Journal of Geodesy, 79, Pages 467–478.
Tenzer, R. and Klees, R. (2008). The choice of the spherical radial basis functions in local gravity field
modelling. Studia Geophysica et Geodaetica, 52, Pages 287–304.
Tikhonov, A. and Arsenin, V. (1977). Solutions of Ill-posed Problems. John Wiley & Sons, New York.
Torge, W. and Müller, J. (2012). Geodesy. Walter de Gruyter. Berlin/Boston.
van Loon, J. (2008). Functional and stochastic modelling of satellite gravity data. PhD thesis, Technical
Universtiy of Delft.
van Loon, J. and Kusche, J. (2005). Stochastic model validation of satellite gravity data: A test with CHAMP
pseudo-observations. In C. Jekeli, L.-M. Bastos, and J. Fernandes (Ed.), Gravity, Geoid and Space Missions,
IAG proceedings, Volume 129, Pages 24–29. Springer.
130
Bibliography
Vanicek, P. and Krakiwsky, E. (1982). Geodesy;the concepts. North-Holland Publishing Company.
Vermeer, M. (1989). FGI studies on satellite gravity gradiometry. 1. Experiments with a 5-degree buried masses
grid representation. Technical Report, Finish Geodetic Institute.
Voigt, C. (2012). Astrogeodätische Lotabweichungen zur Validierung von Schwerefeldmodellen. PhD thesis,
Faculty of civil eingineering and geodesy, University of Hanover.
Weightman, J. (1965). Gravity, geodesy and artificial satellites, A unified analytical approach. G. Veis (Ed.),
The Use of Artificial Satellites for Geodesy, Proceedings of the International Symposium, Athens, Greece,
April 27-May 1, 1965, Volume 2.
Wittwer, T. (2009). Regional gravity field modelling with radial basis functions. PhD thesis, Technical
Wolff, M. (1969). Direct measurements of the Earth’s gravity potential using a satellite pair. Journal of
Geophysical Research, 74, Pages 5295–5300.
Xu, G. (2010). Sciences of Geodesy - I, Advances and Future Directions. Springer.
Xu, P. (1998). Truncated SVD methods for discrete ill-posed problems. Geophysical Journal International,
135, Pages 505–514.
Xu, P. (2009). Iterative generalized cross-validation for fusing heteroscedastic data of inverse ill-posed
problems. Geophysical Journal International, 179, Pages 182–200.
Yarlagadda, R. (2010). Analog and Digital Signals and Systems. Springer.
Zaho, Q. (2004). Research on precise orbit determination theory and software of both GPS navigation
constellation and LEO satellites. PhD thesis, School of geodesy and geomatics of Wuhan University.
Zhu, S., Reigber, C., and König, R. (2004). Integrated adjustment of CHAMP, GRACE, and GPS data. Journal
of Geodesy, 78, Pages 103–108.
Acknowledgement
First of all, I would like to express my gratitude to Jakob Flury for his decent supervision and helpful advices
during my PhD studies. Without his many ideas, steady support and incentives, this work would not have been
possible. I also appreciate the freedom he gave me for choosing the topic and following my research interests.
Especial thanks go to Jürgen Müller for providing me the opportunity to do my research studies in the Institut
für Erdmessung and supporting me in the whole PhD period.
I am also indebted to Michael Schmidt for hosting me several times in Deutsches Geodätisches
Forschungsinstitut (DGFI) in Munich as well as for a series of technical discussions within his research group.
His willingness to review and correct my thesis is highly appreciated. Furthermore, I would like to thank
Gerhard Heinzel and Ingo Neumann for accepting to be in the exam committee and for giving me constructive
feedback and comments in the exam and in their reviews on my thesis. Appreciation is extended to Phillip
Brieden for providing the real GOCE orbit and calibrated GOCE gravity gradients as well as for providing the
German version of the Summary. Many thanks go to my colleagues at Institut für Erdmessung for their help
and encouragements.
This work has been carried out in the framework of the fellowship program of the Centre for Quantum
Engineering and Space-Time research (QUEST). QUEST is a cluster of excellence funded by the Deutsche
ForschungsGemeinschaft (DFG). It is a joint venture of the Leibniz Univeristät Hannover, the Max Plank
Institute for Gravitational Physics, the Physikalisch-Technische Bundesanstalt (PTB) and several other research
institutes. The outstanding support by the QUEST office in all administrative matters, especially by Birgit
Ohlendorf, is gratefully acknowledged.
Last but not least, I would like to thank my parents for their generous and devotional supports in all periods of
my life. I especially thank my wife, Mina, for her understanding, patience and support during the preparation
of this thesis.
Curriculum Vitae
• Since May 2013: Academic staff, Institute of geodesy, University of Hanover, Germany
• November 2008-April 2013: PhD scholarship holder, Centre for Quantum Engineering and Space-Time
Research (QUEST), University of Hanover, Germany
• September 2004-January 2007: Master of Science in geodesy, K.N.T University of technology, Tehran,
Iran
• September 1999-May 2004: Bachelor of Science in surveying engineering, K.N.T University of technology,
Tehran, Iran
• September 1995-January 1999: High school diploma in physics and mathematics, Towhid high school,
Tehran, Iran
• September 1987-May 1995: Primary and guidance school, Dorood/Tehran, Iran
• August 1981: Born in Tehran, Iran
I, Majid Naeimi, hereby certify that this thesis, has been written by me and contains no material that has been
submitted previously, in whole or in part, for the award of any other academic degree or diploma. Except where
otherwise indicated, this thesis is my own work.

Majid Naeimi - Deutsche Geodätische Kommission

Transcription

Similar documents

Free-air gravity

The Shape of the Earth

Throw a ball up and it will fall down 1) The force of gravity pulls the

Info Sheet - DuClaw Brewing Company

gravity is stronger here

Structural analysis of the Gravity Tripod and a path to a new offshore

The School of Visual Arts presents "Off-Course