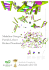as a PDF
Transcription
as a PDF
International Journal of Innovative
Computing, Information and Control
Volume 2, Number 4, August 2006
c
ICIC International °2006
ISSN 1349-4198
pp. 885—896
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK BASED
ON DNA COMPUTING
Ikno Kim, Don Jyh-Fu Jeng and Junzo Watada
Graduate School of Information, Production and Systems
Waseda University
2-7 Hibikino, Wakamatsu-ku, Kitakyushu-shi, Fukuoka 808-0135, Japan
octoberkim@akane.waseda.jp; jeng@fuji.waseda.jp; watada@waseda.jp
Received July 2005; revised November 2005
Abstract. Employees’ tasks have been changing according to the current times by technical development and reform in complicated human relationships, and their capabilities
and abilities are also continuing to improve. Therefore, the necessity for a competent
rating to qualitatively understand relations between employees arises. In this paper, we
select a model of a workplace where employees are sharing information from a variety of
workplaces, and we suppose a personnel network which contains their relations in terms
of mutual understanding. Some subgroups are sure to exist in this employee personnel
network, and the personnel network can be improved by redesigning all the cliques of subgroup networks. However, with a huge number of employees it becomes extremely hard to
find the maximum clique in the personnel network, meaning this problem is NP-hard. All
cohesive subgroups can be found by making the best use of DNA-based computing, also
known as molecular computation, which is a new approach to massively parallel computation. DNA computing is drawing attention from many researchers around the world.
The goal of this paper is to propose a way to apply DNA computing, one of the new
biotechnologies, to human resource management that is a part of the management engineering field, and to measure the efficiency of DNA computing in redesigning subgroups
to support work rotation.
Keywords: Subgroup, Personnel network, Work rotation, Clique, DNA computing
1. Introduction. Routine tasks that are very specialized, such as assembly-line positions, hold limited appeal in advanced industrial societies. Rarely do these routine tasks
offer opportunities for achievement, recognition, psychological growth, or other sources
of satisfaction. To enhance the quality of work life for those who hold such responsibilities, human resource managers can use a variety of methods to improve tasks. The most
widely practiced technique includes work rotation [1,2]. Work rotation moves employees
from task to task. Tasks themselves are not actually changed a lot, only the employees are rotated. Rotation breaks the monotony of highly specialized work by calling on
different skills and abilities. The organization benefits because employees become competent in several tasks rather than only one. Knowing a variety of tasks improves the
employee’s self-image, provides personal growth, and makes the employee more valuable
to the organization.
The most important point is to note all the subgroups [3] in the personnel network to
execute work rotation. The most important reason is that the personnel network might
885
886
I. KIM, D. J. JENG AND J. WATADA
become a huge number of employees composed of all the connected subgroups, and those
subgroups are also composed of subgroups, both small and large. Another important
reason is that human resource managers hope to find the maximal number of employees
who mutually exchange and share their information by close interpersonal relationships at
work. However, even if employees’ close interpersonal relationships in the huge personnel
network are known, it would be quite difficult to redesign all the subgroups efficiently,
because the maximum cliques [4] from all the subgroups in the huge personnel network
must be extremely hard to discern exactly. Furthermore, finding the maximum clique
of employees becomes NP-hard, and cannot be solved using present electronic computers
in polynomial time unless P=NP, which is widely believed to be false. Ordinarily, the
majority of human resource managers redesign subgroups statistically based on either
the frequency of employees’ relationships or managers’ experiences. To address this, we
use DNA computing to solve these redesign problems of the subgroups in the personnel
network.
DNA computing has drawn attention in various fields [5,6] since it was proposed to be
able to solve a Hamiltonian path with molecular computation by L. Adleman in 1994 [7].
Until now, there are no cases that apply to management problems. The attention is almost
entirely from either the computer science fields or the biotechnology fields. However, we
argue that DNA computing should be a very useful tool for a variety of management
problems. Thus, we have shown that efficient solutions are obtained by DNA computing,
and the efficiency of DNA computing is examined by redesigning subgroups in a personnel
network to solve one of the management problems.
2. Analysis of Subgroups. A personnel network is composed of various types of subgroups. It is necessary to analyze all the subgroups to accurately understand the personnel
network. Therefore, in this section, we describe and analyze subgroups in more detail to
provide a better understanding of this personnel network problem.
2.1. Cohesive subgroups. Cohesion is closely related to concepts of strong ties among
members of embedded social groups or closed social circles. Cohesive subgroups [3] are
subsets of actors among whom there are relatively strong, dense, direct, frequent, intense,
or positive ties. These are relations that enable employees to share or exchange their
information, create solidarity, or act collectively. Numerous direct contacts among all
cohesive subgroup employees, combined with few or null ties to outsiders, dispose a group
toward a close interpersonal relationship in business, homogeneity of thought, behavior,
and identity. Examples of formal cohesive groups include the personnel department,
production department, quality control department, and finance department, whereas
informal cohesive groups include religious cults and hobby clubs.
Structural variables are measured on a single set of actors, such as relationships among
employees give rise to one-mode networks, whereas there are types of structural variables
that are measured on two sets of entities, such as actors of employees from different sets,
one set consisting of corporations and a second set consisting of non-profit organizations.
It could be measured the flows of financial support flows from corporations to non-profit
employees. These two sets of employees are referred to as a two-mode network. A onemode network is the most common type of personnel network since all actors of employees
come from only one set. Cohesive subgroups in one-mode networks focus on properties of
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK
887
pair-wise ties, whereas cohesive subgroups in two-mode affiliation networks focus on ties
existing among employees through their joint relationships in organizations.
Figure 1. Presonnel network and nodal degrees for employees’ relations
2.2. Cliques. A cohesive subgroup should have a clique that is a useful starting point
for specifying the formal properties. The clique also has well-specified mathematical
properties, and captures much of the intuitive notion of cohesive subgroups. In a graph,
the clique is a maximal complete subgraph of three or more nodes, and it consists of a
subset of nodes, all of which are adjacent to each other, and there are no other nodes that
are also adjacent to the employees of the clique.
The most common concept for real personnel networks is the n-clique, which is much
closer to people’ everyday understanding of the word ‘clique’. In this concept, n is the
maximum path length at which employees of the clique will be regarded as connected.
Thus, a 1-clique should be the maximal complete subgraph itself, and the subset in which
all pairs of points are directly connected at distance only 1. On the other hand, a 2clique should be one in which the employees are either directly connected at distance 1
or indirectly connected at distance 2 through a common neighbor.
2.3. Maximum clique. A complete graph is a simple graph where an edge connects
every pair of nodes in graph theories. A graph G = (N , E) is complete if all its nodes are
pair-wise adjacent. A clique C in a graph G is a subset of nodes N such that the induced
graph G(C) is complete. That is, there is an edge between every pair of distinct nodes
in N . Clique problem takes a graph G and an integer k as input and asks whether there
888
I. KIM, D. J. JENG AND J. WATADA
is a clique in G of size at least k. The cardinality of C is the number of nodes contained
in C, denoted by |C|. Thus, the objective of the maximum clique is to find a clique
of maximum cardinality in G. Furthermore, the maximum clique can be represented in
the maximum number of employees who mutually exchange and share their information
by close interpersonal business relationships, also the inclusiveness and the density of a
complete relational graph should be 1 in the maximum clique.
2.4. Model graph of personnel networks. We select actors of employees in the same
firm to create their own personnel network based on employees’ records and descriptions.
This personnel network is a highly skilled group in a consulting firm that was first organized by the human resource manager, and was made for providing thoughtful leadership
and specialized support to the firm’s knowledge management consultants; the group was
composed of employees who had advanced degrees or extensive industry experience in
technical fields.
The network for this model is given in Figure 1. In the graph, there are N = 20
nodes, and E = 32 edges between the pairs of nodes. Even with as few as twenty actors of employees and thirty-two ties, the graph looks very complicated. There are also
the four circles that represent present subgroups which do not really look like cohesive
subgroups, and the connected lines that represent the relationships among the employees
who mutually exchange and share their business information through a close interpersonal
relationship in business. Although this personnel network is very intricately connected
with four subgroups, it is important for the human resource manager to redesign better
subgroups by finding a subgroup of all the cliques including the maximum clique, in order
to satisfy work rotation requirements with a new personnel network.
3. DNA Computing Approach. DNA computing is recently drawing attention from
a number of scientists, engineers and other researchers [8-10]. The attention is almost
always focused on solving NP-completeness problems, combinational problems and difficult mathematical problems. However, we propose a way to solve one of the management
problems using DNA computing. Therefore, in this section, we describe how to relate
employees to DNA sequences, and how to approach redesigning subgroups based on a
DNA experiment.
Figure 2. Watson-crick complementarity
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK
889
3.1. DNA computing. DNA computing is that using bio-molecules as a support for
devising computers and computations, a new approach to massively parallel computation.
In 1994, L. Adleman discovered a way to solve the Hamiltonian path problem, which is
one of the NP-complete problems, using only biochemical techniques. He used DNA to
solve a 7-node, a special case of an NP-complete problem that attempts to visit every
node in a graph exactly once.
Deoxyribonucleic acid consists of polymer chains, call DNA strands, that are composed
of nucleotides adenine (A), guanine (G), cytosine (C) and thymine (T). Adenine always
bonds with only thymine, while guanine always bonds with only cytosine. This phenomenon is called Watson-Crick complementarity.
3.2. Algorithm to find cliques. Basically, the ideas of analyzing and designing cohesive
subgroups can define specific graph theoretic properties that should be satisfied in order
to identify a subset of employees. For these kinds of approaches to cohesion in personnel
networks, examining a set of personnel network data is to find collections of employees who
have relatively strong ties, and it becomes visible by displaying functions or rearrangement
of these networks. We note one of the approaches to cohesive subgroup analysis that is a
socio-matrix [11], because this is the most important analyzing procedure to find all the
cliques of the subgroups using DNA computing.
A systematic way for ordering rows and columns of the socio-matrix reveals the subgroup structure of the personnel network. Figure 3 shows a socio-matrix of the model
graph with the rows and columns, employees who have ties and close interpersonal business relationships to each other in the socio-matrix. The socio-matrix of size m × m
becomes 20 rows and 20 columns for the model graph. There is a row and column for
each node, and the rows and columns are labeled 1, 2, 3,. . . , 20. xij denotes the value of
the tie from employee i to employee j, and xij records which pairs of nodes are adjacent.
If nodes Ni and Nj are adjacent, then xij = 1, and if nodes Ni and Nj are not adjacent,
then xij = 0. In addition, an edge between two nodes is either present or absent. If an
edge is present, it goes both from Ni to Nj and from Nj to Ni , thus, xij = 1, and xji = 1.
The total sum of rows and columns represents the level of the connections between edges,
which is divided by 2, becomes
L=
m
m P
P
i=1 j=1
2
xij
f or
i 6= j
(1)
where the number of edges corresponds to L. As shown in Figure 3, the total sum of rows
and columns is 64, which means the number of edges should be 32. The number of edges
should be equal to the number of all the independent lines in a 2-node. Furthermore,
the connectivity matrix for 20 employees shown in Figure 1 is the 20 × 20 socio-matrix
in Figure 3. This socio-matrix makes the best use of this DNA application because it is
simple, and easy to understand how many DNA fragments and sequences we will need for
the DNA experiment.
We designed a new algorithm based on the socio-matrix in Figure 3 and the algorithm
of the maximal clique problem solution that was proposed by Q. Ouyang [8], the method
to find the maximum clique. However, the new algorithm that finds all the 1-cliques, as
890
I. KIM, D. J. JENG AND J. WATADA
Figure 3. Socio-matrix for the personnel network of 20 employees
well as the maximum clique, because we would like to design more cohesive and efficient
subgroups in the personnel network based on the DNA results.
Step 1: For a graph with N nodes, each possible clique is represented by a binary
number, which 1 is in the clique, and 0 is vise versa. Also, if the total is 1, 1 is in the
independent line.
Step 2: Create all the possible combinations from 2N ; in this case, it becomes 220 =1048576
where N=20.
Step 3: The graph containing all edges missing in the original graph is called the
complementary graph. Any two nodes connected in the complementary are illegally connected in the original graph. Remove those cliques and independent lines that contain
illegal connections, corresponding to xij = 0 in Figure 3.
Step 4: Sort the remaining data pool to select the DNA-sequence from 2 bits of value
1 to 20 bits of the value 1 in existence.
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK
891
Step 5: Find the nodes that connected between the possible cliques, and distinguish
those connected cliques from other cliques.
3.3. Experiment. In this experiment, the DNA-sequence is designed in the form of
double-stranded DNA, and it corresponds to 20 nodes while satisfying the given algorithm
above. Each node of the DNA-sequence in a binary number is composed of two sequences
that are a position sequence Ei and a value sequence Ni . The position sequences are
used for connecting each node of the DNA-sequence, and the value sequence is used
for distinguishing whether those position sequences contain that node or not. For a
twenty-digit binary number in the graph, twenty value sections (N1 to N20 ) are prepared
sandwiched sequentially between twenty-one position sections (E1 to E21 ). To amplify
the DNA sequence using polymerase chain reaction (PCR), the last section E21 is needed.
We set Ei with the length of 10 base pairs (bp), Ni with the length of 0 bp if the value of
1, and 6 bp if the value of 0. In this case, the longest DNA has 330 bp, and the shortest
DNA has 210 bp. As Table 1 shows, we created 40 oligonucleotides for the experiment.
Each oligonucleotide consists of two different position motifs, Ei Ni Ei+1 for odd i, and
Ei+1 Ni Ei for even i, where the boxed represents the complementary sequence, and the
value of Ni can be 1 or 0. The 40 fragment oligonucleotides were mixed together for
thermal cycling.
We need to remove the complementary sequences that contained illegal connections.
Therefore, as Table 2 shows, we selected the 20 restriction enzyme sites through on technical references that are provided from New England BioLabs.
Finally, we repeat selecting the shortest DNA strands, which correspond to all the
possible cliques using a gel electrophoresis apparatus.
3.4. Experiment results. The experiment in repetition was able to find all the possible
cliques including the maximum clique in the test tube. We decide the size of the clique by
seeing the length of DNA strands. The clique of largest size is represented by the shortest
length of DNA. As Table 3 shows, the maximum clique is {N2 , N7 , N9 , N18 , N20 }, which
is connected at distance 300 bp by five nodes. The second largest clique is {N3 , N8 , N10 ,
N19 }, which is connected at distance 306 bp by four nodes. There are also six possible
cliques that are all connected by three nodes, and the two independent lines with a 2-node
were
found as well. In addition, there are some nodes that represent empty black boxes which
are vertically arranged in Table 3, so we can understand the possible cliques which are
mutually connected together and find out all the nodes are divided into three components
that also can be a component and two subgroups.
4. Redesign of Subgroups. Although there are many different kinds of cliques in a
huge and complicated network, we hope to find all the cliques, and we hope to arrange
them in the large order of cohesion. Moreover, even though we do not know exactly
which cliques connect with which others or how connected subgroups are in the network,
we hope to redesign subgroups efficiently.
4.1. Personnel network analysis. All these problems have been known from the results
of the DNA experiment results. The personnel network is redesigned based on all the
DNA experiment results, as shown in Figure 4. To prove the efficiency of the redesigned
892
I. KIM, D. J. JENG AND J. WATADA
Table 1. Restriction enzyme sites are indicated by underlining and value
sequences Nij , where j indicates the value of Ni . The value sequences are
written with outlined letters.
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK
893
c
Table 2. 20 restriction enzyme sites °New
England BioLabs Inc.
Table 3. Experiment results of the DNA-sequences for 8 cliques and 2 lines
personnel network using DNA computing, we show the differences between the redesigned
personnel network and the previous personnel network. Therefore, we calculated the
inclusiveness and the density of the both personnel networks [12].
Recall that a complete graph is one in which all the nodes are adjacent to one another.
The concept of density is an attempt to summarize the overall distribution of edges in
order to measure how far from this state of completion the graph is.
First, inclusiveness defines the number of nodes that are included within the various
connected parts of the graph. The inclusiveness of a graph is the total number of nodes
minus the number of isolated nodes. The most useful measure of inclusiveness for
comparing various types of graphs is the number of connected nodes expressed as a
proportion of the total number of nodes. Thus, the proportion of the inclusiveness is
894
I. KIM, D. J. JENG AND J. WATADA
Figure 4. Redesigned personnel network and nodal degrees for employees’ relations
denoted by Π, and the inclusiveness is calculated as follows:
n
X
Ni f or 0 ≤ Π ≤ 1
Π = C/
(2)
i=1
where C is the number of connected nodes.
Secondly, the density of a graph is defined as the number of edges in a graph. The
density also expressed as a proportion of the maximum possible number of edges. The
density is denoted by ∆, and the density is calculated as follows:
L
∆=
f or 0 ≤ ∆ ≤ 1
(3)
n(n − 1)/2
where there are n(n − 1)/2 possible unordered pairs of nodes, and thus n(n − 1)/2 possible
edges that could be presented in the graph. Table 4 shows the results of the inclusiveness,
the density, and others for the both personnel networks.
4.2. Analysis results. As Figure 4 shows, it is known that the new subgroup 1 and
subgroup 2 are connected by the relations between the two employees, N3 (Yoshiro) and
N20 (Seiji). These two employees are appropriate to be information communicators, to
exchange their information between subgroups 1 and 2. In addition, subgroups 3 and
4 show that, if the number of degrees is considered, N16 (Yasuo) could be a leader for
subgroup 3, and N13 (Gohei) could be a leader for subgroup 4. Furthermore, it can be
said that, if the four employees who are N20 (Seiji), N3 (Yoshiro), N16 (Yasuo), and N13
(Gohei) are connected, the network could be an integrated personnel network.
REDESIGNING SUBGROUPS IN A PERSONNEL NETWORK
895
Table 4. Inclusiveness and density comparisons
Finally, following the results in Figure 4 and Table 4 we can measure the efficiency
of DNA computing in redesigning subgroups. Thus, it is better to use DNA computing
rather than Figure 1 when human resource managers redesign subgroups in any kinds of
personnel networks or other social networks to support work rotation in efforts to improve
the quality of work life.
5. Concluding Remarks. In this paper, the subgroups were redesigned more efficiently
and effectively as shown in the new personnel network. A massively parallel computation
corresponds to DNA computing that was able to be done to make a new personnel network
for an efficient work rotation. In addition, we show various ideas on human resource
management based on the results of DNA computing. On the other hand, there were
some problems, mainly that mistakes often happen in cutting DNA strands, and the
number of nodes is limited to processes with picomole operations.
Further research includes investigating DNA computing for nodes in signed or valued
graphs to develop a proactive systematic approach to solving a real personnel network
problem, and expanding the different kinds of applications for managerial problems from a
variety of industrial and management fields in order to support optimal decision-making.
REFERENCES
[1] Umezu, H., MBA Management of Human Resources and Organization, Seisansei-Shuppan, pp.137157, 2003.
[2] Werther, W. B., Jr. Werther and D. Keith, Human Resources and Personnel Management, McGrawHill, Inc., pp.145-157, 1995.
[3] Wasserman, S. and K. Faust Social Network Analysis, Cambridge University Press, pp.149-290, 1999.
[4] van Noort, D., F.-U. Gast and J. S. McCaskill, DNA computing in microreactors, submitted to
Special Lectures in DNA Computing, The Graduate School of Information, Production and Systems,
Waseda University, pp.1-10, 2005.
[5] Jeng, D. J.-F., J. Watada and I. Kim, Solving a real time scheduling problem based on DNA computing, Proc. of the 2005 International Conference on Intelligent Technologies and Applied Statistics,
Taipei, Taiwan, pp.317-322, 2005.
[6] Liu, Q., L. Wang, A. G. Frutos, A. E. Condon, R. M. Corn and L. M. Smith, DNA computing on
surfaces, Nature, vol.403, pp.175-179, 2000.
[7] Adleman, L., Molecular computation of solutions to combinatorial problems, Science, vol.266,
pp.1021-1024, 1994.
[8] Ouyang, Q., P. D. Kaplan, S. Liu and A. Libacher, DNA solution of the maximal clique problem,
Science, vol.278, pp.446-449, 1997.
896
I. KIM, D. J. JENG AND J. WATADA
[9] Sakamoto, K., D. Kiga, K. Komiya, H. Gouzu, S. Yokoyama, S. Ikeda, H. Sugiyama and M. Hagiya,
State transitions by molecules, Biosystems, vol.52, pp.81-91, 1999.
[10] Ibrahim, Z., Y. Tsuboi, M. S. Muhammad, O. Ono and M. Khalid, Parallel overlap assembly for
initial pool generation of direct-proportional length-based DNA computing, International Journal
of Innovative Computing, Information & Control, vol.1, no.2, pp.261-275, 2005.
[11] Carrington, P. J., J. Scott and S. Wasserman, Models and Methods in Social Network Analysis,
Cambridge University Press, pp.77-97, 2005.
[12] Yasuda, Y., Practice Network Analysis, Shinyosha, pp.55-63, 2004.