Atomistic Friction Phase Diagram and Non

The 14th IFToMM World Congress, Taipei, Taiwan, October 25-30, 2015 DOI
Number: 10.6567/IFToMM.14TH.WC.OS18.011
Atomistic Friction Phase Diagram and Non-linear dynamical effects in dynamic
frictional energy dissipation
M. Hirano∗
Hosei University
Koganei, Tokyo, Japan
Abstract— Friction is a phenomenon observed ubiquitously in daily life, yet its nature is complicated. Friction
between rough surfaces is considered to arise primarily because of macroscopic roughness. In contrast, interatomic
forces dominate between clean and smooth surfaces. “ Superlubricity ”, where friction effectively becomes zero, occurs when the ratio of lattice parameters in the pair of surfaces becomes an irrational number. Superlubricity has
been found to exist in a limited number of systems, but is
a very important phenomenon both in industry and in mechanical engineering. New atomistic research on friction is
under way, with the aim of refining theoretical models that
consider interactions between atoms beyond mean field theory and experiments using ultrahigh vacuum non-contact
atomic force microscopy. Such research is expected to help
clarify the nature of microscopic friction, reveal the onset
conditions of friction and superlubricity as well as the stability of superlubricity, discover new superlubric systems,
and lead to new applications.
S. Kim
Hosei University
Koganei, Tokyo, Japan
perature affects the sliding properties in friction and superlubricity regime.
II. Friction and atomistics
The work from friction has very different properties from
the work from gravity. Work from gravity happens when
objects are moved against gravity, which is always acting
on objects. In contrast, friction is the force required to move
objects perpendicular to the direction of gravity. Once sliding motion starts, friction appears as resistance against the
sliding motion and results in work from friction. Therefore,
friction has the interesting property that it appears when objects start sliding and disappears when objects stop. Even
in interatomic forces, no work from friction is generated as
long as the combined interatomic force is perpendicular to
the sliding direction. The British physicist Tomlinson [2]
was the first to explain this finding at the start of the 20th
century, at around the same time as the British chemist Dalton established the modern atomistics.
Keywords: Atomistics of friction, Superlubricity, Non-linear effect
I. Introduction
The atomistic origin of friction forces stemming from
interfacial atomic-interactions has been investigated from
both of theoretical and experimental viewpoints[1]. By
studying frictional properties of nano-structured materials,
novel understandings explaining the atomistic mechanisms
of static/dynamic friction and those of superlubricity appearing at incommensurately contacting surfaces have been
obtained. For applying the superlubricity mechanisms for
practical use, it is crucial to determine the conditions for
its appearance, describing how we design and synthesize
superlubric systems. To this end, we need to develop realistic interatomic potentials of metals and semiconductors,
and also develop the tribological molecular dynamics simulation at elevated-controlled temperature. This study has
presented the atomic-scale friction simulation at elevated
temperature. The friction diagram, specified by the parameters of sliding velocity and adhesive interaction has been
investigated. Two regimes such as friction and superlubricity appear and it has been examined how atmospheric tem∗ hirano@hosei.ac.jp
Fig. 1. Tomlinson model. It has been considered that two solid bodies in
contact and with relative sliding motion, and for simplicity a single atom D
forming part of a body which is moving in the direction of EF past another
body, of which B and C form two atoms in the state of equilibrium characteristic of a solid. Let us suppose that the atoms D in moving past B along
the line EF approaches B to within a distance of the attraction field but
outside the range of the repulsion. The passage of D causes a slight disturbance in the position of B, which moves away from C, supposing C to be
fixed. The atom D in proceeding further along EF then withdraws from B,
which returns to its original position. It is conceivable that B arrives back
to its original position with some appreciable velocity and therefore with
some added energy, the aggregate of which might correspond to the loss
of energy in friction.
The modern atomistics was established after physics
reached the level of atoms in the 19th century. Physics
started to consider atoms around the mid-19th century although the original concept of atomistics itself, which is
that matter consists of atoms, is thought to have emerged
in ancient Greece as “particle philosophy”. The British
physicist-chemist Boyle tried to use “particle philosophy”
as the foundation of chemistry, and his attempt to build
chemistry upon particle philosophy materialized in the
early 19th century as Dalton’s atomistics. Dalton postulated
that objects with size that are touched daily, regardless of
whether the objects are in gas, liquid, or solid form, consist
of a vast number of very minute particles or atoms bound
together by interatomic force. He thought that there is attraction and repulsion between atoms and that the balance
between these opposing forces results in the three states of
gas, liquid, and solid. The attraction and repulsion between
atoms was later explained based on the concept of electron energy levels and electron states in quantum mechanics. Dalton ’s atomistics was improved through corrections
by Avogadro and others. Although there were opponents to
atomistics, it explained many experimental findings about
the materials properties of gases, Boyle’s law, diffusion and
viscosity of gases, laws on heat conductivity, and the law
of increasing entropy. Atomistics later provided an important foundation for problems regarding the nature of heat.
Physicists such as Helmholtz came to believe that atoms
govern thermal motion.
Tomlinson’s paper states early on that “friction is generally recognized to happen because of interactions between
molecules that are very close to each other”. He investigated the forces that appear in relative motion of atoms in
the field of interatomic interactions at the friction surface,
and succeeded in rationally explaining the problem of how
friction arises from interatomic interactions at the contact
surface, or how mechanical energy dissipates into heat energy due to friction, by introducing the concept of “adiabaticity”, thereby opening the door to the atomistic theory
of friction. Figure 1 shows the original model in the paper.
However, very little research on the atomistics of friction
followed because of the difficulty of handling the complexity of actual surfaces based on the theory.
Friction research changed completely with recent advances in nanotechnology. Friction research in ideal systems where many factors of friction are identified has been
difficult for experimental technology reasons; however, recent measurement technologies, including scanning probe
microscopy and technologies to control clean surfaces under ultrahigh vacuum, have enabled direct comparison between theoretical models and experiments. Theory can
investigate in detail the fundamental properties of interatomic interactions and the mechanism of friction generation using computational experiments on atomistic models.
Therefore, “ideal friction experiments”, where the causes
of friction are accurately identified, can be combined with
“atomic scale friction simulations”, and thus the adequacy
of atomic scale friction theory can now be directly verified.
For example, atomic force microscopy can accurately measure the friction between the surface of a needle tip attached
to the end of a cantilever and the surface of a sample using
the optical lever method, which is a displacement measurement method. The latest experimental devices have enabled
the first observations of friction without wear or fracture.
Conventional adhesion theory cannot be used to investigate
such friction without wear, and therefore it was necessary
to clarify the origins of friction in terms of atomistics.
III. Micro canonical friction system
A. Atomistic model
The atomistic friction model, given by
H({pi }, {ri }) =
N
∑
p2
i
i
+
N
∑
i
2
(1)
f
1
sin(2πri )},
{ k(ri+1 − ri − ℓ)2 +
2
2π
is studied. pi , k, ℓ and f stand for momentum, inter-atomic
interaction, the mean distance between two adjacent atoms,
and adhesive interaction. This is one-dimensional FrenkelKontorova model with kinetic energy terms. The periodicity length of the sinusoidal potential in Eq.(1) is taken as
a unit.The Frenkel-Kontorova model has been studied by
many workers. It is known that this model shows nonadiabatic motion of atoms at f ≈ 0.14, which is often called the
Aubry transition. The dynamics in friction has been studied by adding the kinetic energy terms to the model. To
examine the friction properties including superlubricity, the
dynamics has been studied after the upper solid surface at
the ground state is pushed with initial sliding velocity P (0)
, that is, the Hamiltonian dynamics conserving the energy.
The dynamics is studied by examining quantities such as
P (t) and Q(t), and the sliding distance defined as the distance over which the upper solid surface slides during time.
These quantities are obtained by solving Eq. (1). is √
as1+ 5
sumed to be equal to the golden mean number ℓ =
2
.
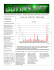
B. Friction phase diagram
Figure 2 shows the how mass center of upper body slide
with time after pushing the upper body at corrupting initial velocity. We could evaluate whether or not upper body
slide with no resistance, thus determining the border between friction regime and superlubricity regime. We obtained the friction phase diagram, shown in Fig.2, representing atomistic-scale frictional properties in terms of two
parameters such as initial velocity and adhesive force.
Two regimes appear in the diagram as shown in Fig.3.
In the superlubricity regime, the superlubric state appears,
i.e., two contacting solid surfaces slide without any resistance. The recurrence phenomenon occurs persistently; this
regime repeats increasing and decreasing the translational
kinetic energy with time. The friction force averaged over
the recurrence time exactly vanishes. The sliding distance
increases linearly with time. On the other hand, in the friction regime, the energy dissipation occurs; the translational
kinetic energy is transferred into the kinetic energy of the
internal motions. The upper surface slides but finally ceases
to slide for sufficiently large times. The friction occurs in
this regime. As P (0) becomes smaller, the sliding distance
decreases for the region f > 0.14. The point at f =0.14 and
P (0)=0 is the Aubry transition point. In the regime f >
0.14, the atoms change their equilibrium positions discontinuously. In the regime P (0)=0 and f < 0.14, the atoms
can slide by changing their equilibrium positions continuously, and the system can slide without any resistance.
Nevertheless, the friction regime spreads over the region
0 < f < 0.14 with finite P (0). This is different from
the result for the original Frenkel-Kontorova model without
any kinetic energy terms, and is due to a dynamic effect of
the system. In particular, the distance, ℓ(∞), over which the
upper solid surface runs till it ceases to slide is ℓ(∞) ≈1 as
the parameters f (> 0.14) and P (0) approach near the horizontal axis, while ℓ(t) tends to stretch with time as one approaches the border line separating the friction regime from
the superlubricity regime. In the friction regime, the temporal behavior of the friction force Fd (t) depends on P (0)
and f in a complex manner. As the parameter f means the
magnitude of the adhesive force between the upper and the
lower solid surfaces, small f corresponds to the weak adhesion. The friction phase diagram in Fig. 3 shows that the
superlubric state appears only for two cases of the weak adhesion and of the high sliding velocity. The property that
the superlubricity appears only for the weak adhesion is peculiar for the one-dimensional system.
Overall, two regimes such as friction regime (F) and superlubricity regime (S) appear in Fig.1. Friction regime has
two sub-area of Fα and Fβ . It seems that the boundaries between F area and S area look like irregular. It will need to
perform a large number of calculations to determine more
beautiful boundaries for successive study. In summary, superlubricity is likely to happen when the intersurface interaction parameter is small because of dynamic effects of
kinetic energy. Interestingly, superlubricity is specifically
unlikely to appear at the range of intermediate velocity (0.3
-0.5) even if the intersurface interaction is small, and a friction regime with different friction properties (Fβ ). The
friction system of multi particles, which are coupled with
each other while feeling the sinusoidal potential when mass
center moves, is essentially non-linear dynamical system.
In superlubricity case, it is easier to evaluate the vibration
mode which looks like simple harmonic oscillation mode,
where a primary vibration peak and the associated higher
order peaks have been verified. Figure.4 shows the FFT
spectrum of the atomic vibration amplitude in superlubricity regime. The primary and secondary peak frequencies
correspond to free vibration ones under the periodic boundary condition, implying that the upper body slides against
lower sinusoidal potential with no friction, while slightly
vibrating at almost natural frequency.
When sliding speed approaches to the region of Fβ area
at small , simple almost harmonic mode turns to be nonharmonic mode when multi vibration peaks have appeared.
The mechanism for the appearance of the multi peaks is
complex problem; it will need to elaborately examine vibration mode signals in terms of non-linear system analysis. A scenario for the transition Superlubricity (S) mode
to Friction (Fβ ) could be described in terms of several nonlinear vibrations such as subharmonic oscillation, summedand-differential harmonic oscillation, superharmonic oscillation, internal resonance phenomena.
In the case of Fα mode, the dynamics of the system has
shown to be chaotic. The occurrence of irreversible energy
dissipation indicates that the internal relative motions are
excited, and hence the adiabaticity does not hold true for
the internal relative motions. In order that the present idea
is adequate, the system must work as a host system absorbing energy. In other words, the dynamic system has the
ergodic property. Our simulations showed that, for the frictional systems of the current interest, the energy seems to be
distributed over the entire degrees of freedoms in the case
of Fα mode.
Mass center
Time
Fig. 2. Frictional properties describing how mass center moves with time.
IV. Canonical friction system
A. Extended molecular dynamics and controlling system
temperature
To examine the temperature effect for the friction phase
diagram property, We adopted the extended system molecular dynamics method developed by Nose [6] to control the
temperature of the atomistic model. In this method the actual atomistic model is contacted against the thermostat,
enabling to make the atomistic model at desired temperature. The extended system method introduced an additional
degree of freedom , which acts as an external system for
where,
1.0
Ps
(8)
Ms
Ms and Ps show the mass and momentum of the thermostat, respectively. The equations of motion (4)-(7) were
numerically solved by using Runge-Kutta method.
Figure 10 shows the calculated result for controlling temperature by Nose thermostat molecular dynamics method.
As shown in Fig.10, it is found that we have successively
controlled the atomistic model temperature at kT =0.1 and
kT =0.2, respectively.
ζ=
Sliding velocity
0.8
0.6
0.4
β
α
0.2
0.0
0.02
0.04
0.06
0.08
0.10
0.12
0.14
Adhesion energy
Fig. 3. Friction diagram showing friction and superlubricity regime obtained by micro canonical ensemble MD calculation. N=1000
Fig. 5. Controlling system temperature.
݇஻ ܶ ൌ ͳǤͲ
Fig. 4. FFT spectrum. N=100.
the physical system of particles, and assumed the following
simple time-scaling.
dt′ = sdt
(2)
The Hamiltonian of the extended system is expressed as follows.
H=
N
∑
p′ i · p′ i
Ps′2
+
Φ
+
+ N kB T log s
2ms2
2Ms
i=1
(3)
The equations of motion for the actual atomistic system
are obtained as follows.
pi
dri
=
dt
m
(4)
dpi
∂Φ
=−
− ζpi
dt
∂ri
(5)
ds
= sζ
dt
(6)
dζ
1
=
dt
Ms
(N
∑ pi · pi
i=1
m
)
− N kB T
(7)
Fig. 6. Friction phase diagram at elevated temperature. • positions belong
to superlubricity region and ◦ positions belong to friction region.
B. Friction phase diagram at elevated temperature
It has been shown that the calculated sliding properties,
representing how the upper body slides after pushing the
body at the specified initial velocity . In superlubricity
regime, as shown in Fig.3, at and , the position of mass center moves at constant velocity. On the other hand, as shown
in Fig.4, as increases the friction appears. It has been found
that the translation kinetic energy of mass center dissipate
into internal relative motion of atoms, and mass center finally stops. This study will discuss how the friction phase
diagram is modified at elevated temperature.
V. Superlubricity and High Dimensionality of Model
Noncontinuous motion of atoms has been demonstrated
not to happen in real Miltiades friction systems. To verify
this, equations of noncontinuous motion were derived and
the motion of atoms in real systems was evaluated to find
out whether motion is continuous or not. Computational experiments of a three-dimensional friction system with realistic interactions showed that adhesion several dozen times
stronger than realistic adhesion is necessary for the occurrence of noncontinuous motion of atoms. Thus, individual
atoms were found to undergo continuous motion is real systems, and superlubricity, or zero friction, was concluded to
appear in infinite systems with incommensurate contact at
the limit of zero sliding speed. Such continuous motion
of atoms arises from the high dimensionality at the contact surface. Dimensionality represents the degrees of freedom of atomic motion at the contact surface. It has been
shown that the stable and unstable areas of atomic motion
at the contact plane. Atoms continuously move at the stable
area, and atoms continue to continuously move near the unstable area because atoms can bypass around the unstable
area. Such flexible motion is achieved by the high degrees
of freedom of atoms. In contrast, one-dimensional systems
have low degrees of freedom of motion, thus any small unstable area encountered during the motion of an atom results in trapping of the atom. This atom moves noncontinuously when moving to the adjacent stable area, resulting in
the generation of friction.
VI. Conclusions
The sliding properties in friction and superlubricity
regime of Frenkel-Kontorova atomistic model has been
examined by the extended system molecular dynamics
method.
1. It has been confirmed that the extended system molecular dynamics method could successfully control the
elevated temperature of the friction model.
2. The sliding properties of the Frenkel-Kontorova
model has been examined at elevated temperature.
Friction and superlubricity appeared as a function of
adhesion and initial sliding velocity.
References
[1]
[2]
[3]
[4]
Bhushan B., Isralachvili J. N. and Landman U. Nanotribology: Friction, Wear and the Atomic Scale. Nature, 374(607–616, 1994.
Tomlinson G. A. A Molecular Theory of Friction. Phil. Mag.,
7(46:905–939, 1929.
Hirano M. Atomistics of friction. Surface Science Reports,
60(8:159–201, 2006.
Nosé S.
A unified formulation of the constant temperature molecular-dynamics methods.
J. of Chemical Physics,
81(1):511–519, 1984.