article in press - CamTools

Transcription

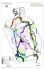
ECOMOD-5004;
No. of Pages 11
ARTICLE IN PRESS
e c o l o g i c a l m o d e l l i n g x x x ( 2 0 0 7 ) xxx–xxx
available at www.sciencedirect.com
journal homepage: www.elsevier.com/locate/ecolmodel
Spatially explicit models to analyze forest loss and
fragmentation between 1976 and 2020 in southern Chile
Cristian Echeverria a,b,∗ , David A. Coomes c , Myrna Hall d , Adrian C. Newton e
a
Departmento de Manejo de Bosques y Medio Ambiente, Facultad de Ciencias Forestales, Universidad de Concepción, Casilla 160-C,
Concepción, Chile
b Núcleo Cientı́fico Milenio FORECOS, Universidad Austral de Chile, Valdivia, Chile
c Department of Plant Sciences, University of Cambridge, Cambridge CB2 3EA, United Kingdom
d Faculty of Environmental Studies, SUNY College of Environmental Science and Forestry, 1 Forestry Drive, Syracuse, NY 13210,
United States
e School of Conservation Sciences, Bournemouth University, Talbot Campus, Poole, Dorset BH12 5BB, United Kingdom
a r t i c l e
i n f o
a b s t r a c t
Article history:
Forest fragmentation threatens biodiversity in one of the last remaining temperate
Received 9 June 2006
rainforests that occur in South America. We study the current and future impacts of frag-
Received in revised form
mentation on spatial configuration of forest habitats at the landscape level time in southern
8 October 2007
Chile. For this purpose, we identify the geophysical variables (“pattern drivers”) that explain
Accepted 23 October 2007
the spatial patterns of forest loss and fragmentation between 1976 and 1999 using both a
GIS-based land-use change model (GEOMOD) and spatially explicit logistic regression. Then,
we project where and how much forest fragmentation will occur in the future by extrapola-
Keywords:
tion of the current rate of deforestation to 2010 and 2020. Both modeling approaches showed
Deforestation
consistent and complementary results in terms of the pattern drivers that were most related
GEOMOD
to deforestation. Between 1976 and 1999, forest fragmentation has occurred mainly from the
Landscape indices
edges of small fragments situated on gentle slopes (less than 10◦ ) and far away from rivers.
Logistic regression
We predict that patch density will decline from 2010 to 2020, and that total forest interior
Temperate forests
area and patch proximity will further decline as a result of forest fragmentation. Drivers
Chile
identified by these approaches suggest that deforestation is associated with observed local
socio-economic activities such as clearance of forest for pasture and crops and forest logging
for fuelwood.
© 2007 Elsevier B.V. All rights reserved.
1.
Introduction
Fragmentation is a dynamic process in which the habitat of
organisms is progressively reduced into smaller patches that
become more isolated and affected by edge effects (Forman
and Godron, 1986; Reed et al., 1996; Franklin, 2001). This process may lead to an increase in isolation of habitats and to a
modification of ecosystem functioning that endangers species
of plants, mammals and birds. Tropical forests have experienced a rapid, unprecedented forest loss and fragmentation
that are having major impacts on wildlife, regional hydrology
and the global climate (Laurance, 1999; Laurance et al., 2002).
Similarly, temperate forests have been affected by land-cover
change reaching high rates of forest loss in the southern hemisphere (Echeverrı́a et al., 2006). In particular, temperate rain
forests in Chile, which are classified as a biological “hotspot”
∗
Corresponding autor at: Departmento de Manejo de Bosques y Medio Ambiente, Facultad de Ciencias Forestales, Universidad de Concepción, Casilla 160-C, Concepción, Chile. Tel.: +56 41 2204936; fax: +56 41 2255164.
E-mail address: cristian.echeverria@udec.cl (C. Echeverria).
0304-3800/$ – see front matter © 2007 Elsevier B.V. All rights reserved.
doi:10.1016/j.ecolmodel.2007.10.045
Please cite this article in press as: Echeverria, C., et al., Spatially explicit models to analyze forest loss and fragmentation between 1976 and
2020 in southern Chile, Ecol. Model. (2007), doi:10.1016/j.ecolmodel.2007.10.045
ECOMOD-5004;
2
No. of Pages 11
ARTICLE IN PRESS
because of their high endemism (Myers et al., 2000), are disappearing as a result of land-cover change. This country has the
largest temperate forest area in South America and more than
a half of the total area of temperate forests in the southern
hemisphere (Donoso, 1993). These forests are being harvested
to supply the increasing global demand for wood and paper
products and to clear areas for crops and pasture land (Lara
et al., 2002). In response to growing concerns over the loss
of biodiversity by fragmentation, specialists are seeking better ways of managing ecosystems at a variety of spatial and
temporal scales (Turner et al., 2001). Growing evidence that
habitat fragmentation may contribute substantially to the loss
of regional or global biodiversity (Saunders et al., 1991) has
provided empirical justification for the need to manage entire
landscapes, not just the individual elements. For this purpose,
landscape ecologists have developed techniques that provide
in-depth analyses of the spatial configuration and compositional diversity of the elements of the landscape (McGarigal
et al., 2002; Bennett, 2003; Herrmann et al., 2005). The development of geographical information system (GIS) techniques
has offered a variety of analytical tools for the analysis at the
landscape level.
Many studies on deforestation and fragmentation analyze the temporal changes at a landscape level in order to
understand the spatial patterns and interactions among the
elements of the landscape and how these patterns change
over time (Franklin, 2001; Staus et al., 2002; Fitzsimmons, 2003;
Echeverrı́a et al., 2006). Also, ground-based studies provide
data that can then be analyzed with respect to changing landscape patterns due to forest fragmentation (Metzger, 2000;
Martı́nez-Morales, 2005; Echeverrı́a et al., 2007) in order to
understand the consequences of these changes on composition and diversity of fragments (Cornelius et al., 2000;
Asbjornsen et al., 2004; Castelletta et al., 2005). However, a
more comprehensive understanding of the underlying drivers
of fragmentation is required in order to inform future policy decision making or for land-use planning. This analysis
must study the drivers responsible for forest loss and fragmentation, leading to the analysis of processes and not merely
patterns (Bürgi et al., 2004). The use of the word “drivers” can
be misleading since there are drivers or forcing functions that
explain root causes and pressure on a system, and there are
spatial pattern drivers, or landscape features, that influence
where fragmentation is likely to occur. We focus on the latter,
those geophysical attributes or landscape characteristics that
determine where humans have chosen to invest their energies in order to survive (i.e. to derive food or income). These
drivers show how the fragmentation has taken place spatially
and temporally in the landscape. The ability to link a particular geophysical variable in the landscape to specific landscape
changes is a powerful tool for researchers exploring environmental change (Evans and Moran, 2002).
Modeling of land-cover changes such as deforestation
requires combining spatially explicit ecological data with
information on socio-economic factors (Dale and Pearson,
1997; Pearson et al., 1999). GEOMOD, a GIS-based model,
can simulate the location of deforested cells using both biogeographical and socio-economic attributes as well as spatial
data of forest cover at different time intervals (Hall et al.,
1995a,b; Pontius et al., 2001). GEOMODs predictions can be
improved by testing estimates of both the quantity of future
forest areas as well as the location (Pontius, 2000). GEOMOD
has the advantage that it does not require large amounts of
data for calibration and validation, compared to other complex dynamic models (Pontius et al., 2001). Another advantage
of GEOMOD over others is its use of validation prior to extrapolation.
Logistic regression has been used to assess the probability
of native forest conversion to industrial plantations in southern Chile (Wilson et al., 2005) and to create suitability maps of
deforestation for the period 1971–1985 in Massachusetts, USA
(Schneider and Pontius, 2001). Comparison of actual change
maps to maps of modeled suitability revealed the ability of this
approach to predict land-use changes. Serneels and Lambin
(2001) used the logistic model to identify the drivers of conversion to agriculture in Narok District, Kenya, and Williams
et al. (2005) applied it to determine the factor influencing the
decline of native grasslands in Australia.
Although analysis and modeling of deforestation are the
focus of a substantial research effort of ecologists, very few
studies have assessed the future impacts of fragmentation
on spatial configuration of forest habitats at the landscape
level by projecting the current trends of forest loss. Furthermore, relatively few studies have sought to compare different
analytical approaches. The objectives of this study are (1) to
identify the geophysical variables that determine forest cover
change in southern Chile’s temperate forests using both GEOMOD and logistic regression; (2) to compare the results of the
two analytical approaches; and (3) to assess the effects of
such variables on the patterns of forest loss and fragmentation projected to the years 2010 and 2020. An understanding
of landscape change is provided by integrating across time the
causal relationships between forest cover change and spatially
explicit variables. We hypothesize that changes in the configuration and area of the forest cover are the result of the
preferred geophysical variables associated with forest logging
and agriculture expansion. Also, we hypothesize that the current trends in deforestation may lead to substantial additional
loss and fragmentation of the remaining forest fragments over
the next decades. This information will be helpful to conservationist and biologists who are currently working on how to
minimize the ecological impacts of ongoing deforestation. It
will also contribute the provision of key information for decision making and management of natural resources.
2.
Methods
2.1.
Study area
The study area covered approximately 500,000 ha located
between 41◦ 30 –42◦ 20 S and 73◦ –74◦ W in southern Chile
(Fig. 1). In the middle of the 20th century a portion of the
native forests was cleared for agriculture as a result of European settlements (Donoso and Lara, 1997). The progressive
deforestation in the landscape since 1985 may be related to
a 400% increase in demand for industrial native forest products from 1988 to 1995 (Lara et al., 2002). This trend is explained
mainly by the evolution of woodchip exports, which increased
from 0.07 millions of tonnes in 1988 to 2.6 in 1995 (Lara et al.,
ECOMOD-5004;
ARTICLE IN PRESS
No. of Pages 11
3
Fig. 1 – Location of the study area in southern Chile.
2002), and by a continuous production of fuelwood for growing municipalities located across the study landscape (Reyes,
2000). Expansion of crops and pastureland since 1970s has also
been recognized as the other main cause of deforestation in
the study area (Lara et al., 2002). In this process, recurrent fires
are used as intermediate agent of conversion of forested areas
to pasture.
The study landscape is also highly representative of the
region in terms of the forest composition. The native forests
are characterized by the presence of several broad-leaved
evergreen tree species such as Amomyrtus luma, Amomyrtus
meli (both Myrtaceae), Drimys winteri (Winteraceae), Eucryphia
cordifolia (Eucryphiaceae), Laurelia philippiana (Moniniaceae),
Nothofagus dombeyi (Nothofagaceae), accompanied by a dense
understory composed mainly of Chilean bamboos (Chusquea
quila and Chusquea spp., Gramineae) and ferns. In some sites,
the long-lived conifers such as Fitzroya cupressoides and Pilgerodendron uvifera (both Cupressaceae and highly threatened
trees) can also be found. All these species grow both on deep
soils of recent volcanic ash or on incompletely drained soil
called Ñadi soil that present a solid iron-silicate-layer at a
depth of 20–80 cm (Janssen et al., 2004).
2.2.
Preparation of the spatial data
To analyze change over a 23-year time period we acquired
and classified a set of three Landsat satellite scenes: 1976
(MSS), 1985 (TM), and 1999 (ETM+). Each image was geometrically, atmospherically and topographically corrected. We used
supervised classification and to assist in the classification of
overlapping signatures, we applied the statistical decision criterion of maximum likelihood in which pixels were assigned to
the class of highest probability (Chuvieco, 1996). The classification of the 1999 image was done using a set of thematic digital
land-cover maps developed by one of the most comprehensive
cartographic studies of natural vegetation conducted in Chile
known as Catastro (CONAF et al., 1999), which covers the periods 1995–1997. A second reference group was comprised of 70
control points of field visits in which land-cover types that did
not show changes in the last 30 years were recorded in July
2002. To carry out a quantitative comparison of the images,
the original 79 m MSS raster grids were resampled to the resolution of the TM and ETM+ raster grids (30 m). The smallest
patches (less than 5 pixels) were removed from all the images
in order to reduce differences in data quality produced by the
resampling of the MSS image.
Images were classified into the following land-cover types:
native forests, crop and pasture lands, shrublands and
arboreus shrublands (both originated after forest logging or
by regeneration in deforested areas), wetlands, water bodies
and other land-cover types such as urban and bare areas. The
overall accuracy of the classification of each image was estimated by constructing confusion matrices between reference
data and classified data (Chuvieco, 1996). The accuracy of the
ETM+ image was assessed by ground validation of 260 points.
For the TM and MSS images, reference data (250 points for
each image) was obtained from forest resource maps developed by the Instituto Forestal in 1979 and from additional field
observations of land-cover types that did not exhibit changes
between images over time. The overall accuracy values corresponded to 88.8% for the 1976 image, 89.6% for the 1985 image,
and 91.9% for the 1999 image. The accuracy of native forests
reached 94.9% in 1976, 95.9% in 1985 and 96.1% in 1999. The
category with the lowest overall accuracy (67%) corresponded
to the category of ‘other’ land-cover types in the 1976 image.
The categories of land-cover types were grouped into the
non-forest and forest categories to create a binary forest/nonforest map using ARC VIEW 3.2 software and its extension
Arc View Spatial Analyst 2.0 for Window (ESRI, Redlands, CA,
USA). In particular, crop and pasture lands, shrublands and
ECOMOD-5004;
No. of Pages 11
4
ARTICLE IN PRESS
arboreus shrublands, wetlands and other land-cover types
were grouped into the non-forest category, and native forests
were grouped into the forest category. The maps were used to
assess the patterns and drivers of forest loss and fragmentation.
2.3.
Landscape spatial pattern analysis
After reviewing recent forest fragmentation studies
(Armenteras et al., 2003; Fitzsimmons, 2003; Imbernon
and Branthomme, 2001; Millington et al., 2003; Staus et
al., 2002), we selected from the landscape indices available
in FRAGSTATS software (Version 3) (McGarigal et al., 2002)
four landscape metrics that we believed would capture the
resulting patterns of fragmentation over space and time. They
included: (a) patch density (number of patches per 100 ha) as
a measure of forest loss and division, (b) total edge length
(km) as a measure of patch shape and the forest to clearance
(cleared land) interface for potential edge effect studies,
(c) total core area (total patch size in hectares) remaining
after removing a buffer edge of 100 m; minimum distance
defined according to previous studies that deal with edge
effect (Millington et al., 2003; Vergara, 2005; Porej et al., 2004)
as a measure of high-quality forest interior habitat, and (d)
mean proximity index (ratio between the size and proximity
of all patches whose edges are within a 1-km search radius
of the focal patch) as a measure of isolation. These landscape
indices were computed at the landscape level using the forest
cover maps generated for each year. A Kruskal–Wallis test
was used to determine if the indices obtained between time
intervals were different at the 95% confidence level (Dytham,
2003).
2.4.
Logistic regression
We identified the areas deforested between each time interval (1976–1985 and 1985–1999) by overlaying the corresponding
binary maps of forest/non-forest cover in a GIS (Fig. 2a). The
binary response variable (forested, deforested) was analyzed
using a logistic regression model. This model uses the following logit link function to transform the linear predictor (the
combination of explanatory variables) to a measurement scale
suitable for binomial data (Crawley, 2005):
log
p 1−p
where p is probability. The probability of deforestation is
expressed by the following model:
p(x) =
e(ˇ0 +ˇ1 X1 +···ˇk Xk )
1 + e(ˇ0 +ˇ1 X1 +···ˇk Xk )
where Xk is the explanatory variable and ˇk is the estimated
parameter of variable Xk .
We selected a suite of nine candidate geophysical variables
that we believe have influenced where people have cleared
forest land for various economic uses over time (Fig. 2a). Most
of these factors influence how much energy people will have
to exert to get to the land and work the land and how much
return they will experience from that investment. The variables selected include: slope, elevation, distance to roads in
1976, distance to rivers, distance to urban areas, soil type, dis-
Fig. 2 – Flux diagrams illustrating the two spatially explicit
modeling approaches used in this study: (a) logistic
regression models and (b) GEOMOD modeling.
tance to land already cleared for agricultural use in 1976, forest
patch size, and distance to forest patch edge. We generated
the first four variables from the Catastro data set at a scale of
1:50,000 (CONAF et al., 1999, Table 1). For soil types we used
digital soil maps at a scale of 1:250,000 developed by Schlatter
et al. (1995) and for maps of distance to 1976 agricultural area,
patch size and distance to patch edge we used the land-cover
maps derived from satellite images. We assumed that the
contribution of these factors to deforestation has operated
from 1976 to 1999 and will operate over the next decades.
The geophysical and response variables were converted to
a raster map of 30 m × 30 m grid cells using ©Arc View software (ESRI). Grid maps were exported into ©R 1.9.0 statistical
software (Dalgaard, 2002) for logistic regression analyses. We
randomly selected a sample of 1000 points for each time interval with the stipulation that they be separated by a distance
of at least 1500 m. This distance lessened the effect of spatial
autocorrelation. A proportion of 29.2% of the sampling points
corresponded to deforested areas for the 1976–1986 period and
40%, for 1985–1999 period. We calculated their independence
using the Moran index and achieved a value of 0.12, where
ECOMOD-5004;
No. of Pages 11
Geophysical
variables
GEOMOD modeling (1985–1999)
Kappa
(unconstrained)
Kappa
(constrained 3 × 3)
Interval 1: 1976–1985
t-value
Intercept
Slope (◦ )
Distance to rivers (m)
Elevation (m a.s.l.)
Soil types
Distance to roads (m)
Distance to urban areas
(km)
Distance to 1976
agricultural areas (m)
Patch size (ha)
Distance to patch edge
(m)
0–5, 5–10, 10–15, 15–20, 20–30,
30–40, 40–90
0–100, 100–200, 200–400,
400–800, 800–1,600,
1,600–3,200, 3,200–6,400,
6,400–12,800, >12,800
0–150, 150–300, 300–450,
450–600, >650
Volcanic ash, Ñadi, Marine
sediments
0–300, 300–600, 600–1,200,
1,200–2,400, 2,400–4,800,
>4,800
0–10, 10–20, 20–30, 30–40, >40
0–200, 400–600, 600–800,
800–1,000 >1,000
–
–
p-value
Interval 2: 1985–1999
t-value
p-value
1.01
−3.83
***
0.5749
0.7426
0.72
−3.37
0.5841
0.7424
–
n.s.
2.39
0.5909
0.7421
−0.86
n.s.
−0.37
n.s.
0.5938
0.7417
–
n.s.
−0.17
n.s.
0.6381
0.7415
−1.69
n.s.
−3.42
n.s.
0.5973
0.7414
0.56
n.s.
0.14
n.s.
0.5944
0.7404
–
n.s.
–
n.s.
–
–
–
–
n.s.
***
−4.41
−4.11
–
–8.01
***
*
***
***
N = 1000 points; *p < 0.01; ***p < 0.001.
ARTICLE IN PRESS
Categories
Logistic regression modeling
5
Table 1 – Attribute maps and/or explanatory variable incorporated in GEOMOD simulations and logistic regression models, respectively. Attribute maps were used in
categories in GEOMOD and as continuous explanatory variables (except for soil types) in logistics regressions. The highest kappa (0.7430) value was obtained by
combining slope and distance to rivers into the simulations. Values of kappa were obtained for simulations constrained and unconstrained by the nearest neighbor
search mode. Variables without t-values correspond to those variables that were not entered in the multivariate logistic model because of their no significance in their
respective univariate models
ECOMOD-5004;
No. of Pages 11
6
ARTICLE IN PRESS
0 indicates no spatial dependence and 1.0 indicates a high
degree of spatial autocorrelation. Variables weakly correlated
(r < 0.5) were selected to fit the logistic models.
For each time interval, we separately entered each
geophysical variable into ©S-PLUS 6.0 statistical software
(Crawley, 2005) to generate a univariate logistic regression
model (Fig. 2a). A variable was retained if the change in
deviance between the model containing the variable and the
null model was significant at a p-value <0.05. Then, the significant geophysical variables were entered into the model
simultaneously to generate a multivariate logistic regression
model for each time interval (Fig. 2a). The function “drop1”
of R was used to assess the significance of the variables in
each model at a p-value <0.05. Drop1 is a backward selection
method available in R that tests the change in deviance against
a 2 distribution.
3.
GEOMOD modeling
GEOMOD selects locations where changes in land uses are
most likely by using three decision rules based on: (a) the
pattern of geophysical variables with respect to already deforested land, (b) stratification by political sub-region, and/or (c)
nearest neighbors. This rule simulates the manner in which
deforestation occurs on the edge or in open areas of forest
fragments.
For the GEOMOD analysis we used the same set of geophysical variables tested in the logistic regression analysis
(Table 1), except patch size and distance to patch edge that
cannot be entered as mapped variables for GEOMOD analysis.
However, distance to patch edge is captured by GEOMODs
nearest neighbor rule, which constrains the selection of cells
to those that lie along the border of forest patches. GEOMOD
constructed a suitability map (areas more vulnerable to be
deforested) based on the degree to which the geophysical variables have determined past deforestation patterns
(Fig. 2b). The suitability map was created in two steps (Pontius
et al., 2001). First, attribute maps were binned into three
to nine categories (Table 1). Second, the model reclassified
each grid cell of each category of the geophysical variable by
assigning a percent-disturbed value, obtained by comparing
the geophysical map to the initial land-use map. GEOMOD
computed the percent-disturbed value of each category (bin)
in the geophysical variable which is the ratio of the quantity
of disturbed grid cells of that category to all cells of that
category in the map. The final suitability map for each model
run is the weighted sum of all reclassified attribute maps to
be used in that run. Hence, we calculated the suitability in
each cell according to the following:
R(i) =
A
a=1
Wa Pa (i)
where R(i) is the suitability value in cell (i), a the particular
geophysical variable map, A the number of geophysical variable maps, Wa the weight of the geophysical variable map a,
and Pa (i) the percent-disturbed in category ak of the geophysical variable a, where cell (i) is a member of category ak . To
avoid assigning an arbitrary importance to the variables, simulations were run using a weight (W) equal to 1 for each variable.
The method of calibration consisted in deriving a simulated
map for 1999, using the 1985 map as a base map and then simulating forest loss at the rate recorded between 1985 and 1999
(Fig. 2b). The iterative process of calibration and validation to
find those variables that yielded the best-fit model consisted
of comparing the simulated 1999 map to the actual map for
the simulated year using the kappa-for-location parameter
(Pontius, 2002) (Fig. 2b). This parameter validates the simulation’s ability to predict location and is equal to 1 when
simulation’s success rate is perfect and is equal to 0 when the
simulation’s success rate is equivalent to that due to chance
(Pontius, 2000). In our case, a “success” occurred when the
grid cell in the map of simulated land-use matched the corresponding grid cell in the actual map in 1999.
The effects of GEOMODs decision rules (nearest neighbor and geophysical variable weighting) were examined using
each variable individually with and without the nearest neighbor mode. The selection of the most important spatial pattern
drivers to be used in the forward projection to 2010 and 2020
was based on those variables that achieved the highest values
of kappa-for-location upon validation against the 1999 map
(Fig. 2b). After selecting the “best-fit” geophysical variables, we
ran simulations of forest cover to 2010 and 2020. The quantity
of future forest cover was determined by linearly extrapolating
the forest loss rate observed in the classified imagery between
1985 and 1999 which amounts to 1691 ha year−1 equivalent
to 0.78% year−1 . It was assumed that both the rate and the
influence of geophysical variables would remain constant over
time. The extrapolated 2010 and 2020 forest cover maps used
for the evaluation of the four landscape indices corresponded
to maps of gross deforestation, as our analysis assumes that
there is no regrowth of deforested areas.
4.
Results
4.1.
Logistic regression models
The multivariate logistic regression model proposed that
the probability of an area being cleared of forest for the
1976–1985 interval was highly significant (p < 0.001) and negatively related to distance from patch edges and slope (Table 1).
The variables considered in the logistic model of deforestation after exclusion of highly correlated variables were patch
size, slope, elevation, soil type, distance to rivers, distance to
patch edge, and distance to towns. In the univariate logistic
regression five variables explained some of the variation in the
pattern of forest cover at p < 0.001, except patch size (2 = 1.8,
d.f. = 1, p = 0.179), distance from river (2 = 2, d.f. = 1, p = 0.157),
distance to 1976 agricultural areas (2 = 1.1, d.f. = 1, p = 0.219),
and soil types (F = 0.095, d.f. = 1, p = 0.922), which did not show a
significant change in deviance. Therefore, these variables were
not entered in the backward selection (no t-value in Table 1).
For the 1985–1999 interval, the probability of deforestation
was related negatively to distance from patch edges, slope and
patch size and positively to distance from rivers (Table 1). During this period, all the explanatory variables were significant,
except distance from 1976 agricultural areas in 1976 (Table 1).
The most powerful predictors were patch size and distance to
patch edge.
ECOMOD-5004;
No. of Pages 11
ARTICLE IN PRESS
4.2.
GEOMOD modeling
Simulations revealed that the most effective decision rule
to model the location of forested cells was the one based
on slope, distance to rivers and the application of a 3 × 3
nearest neighbor deforestation rule (Table 1). In this case, GEOMOD was able to classify correctly 88.04% of the grid cells
(kappa = 0.7430) of the 1999 reference map. Higher kappa values (>0.74) were obtained when the simulations in GEOMOD
(from 1985 to 1999) were constrained to the nearest neighbor
search mode (Table 1). Individually slope yielded the highest
kappa with 0.7426, followed by distance to rivers with 0.7424.
The categories of slope with ranges 0–5◦ presented the
highest percent of deforested cells in 1985 with 58%. The
lowest percent-deforested (7%) was concentrated in slopes
between 20◦ and 30◦ . For areas situated between 200 and
800 m away from rivers, the percent-deforested was 60%. In
forests located between 0 and 100 m from rivers almost 50%
of cells were deforested. With respect to elevation, the majority of deforested cells (58%) were concentrated between 0 and
150 m a.s.l. Only 8% of deforested cells occurred higher than
450 m a.s.l. Although the predictive power of soil type was
lower (kappa = 0.7417), almost 60% of cells situated in volcanic ash soil were deforested, whereas 45% of deforestation
occurred in Ñadi soil. At less than 300 m from the nearest road,
80% of the cells were deforested. For a distance greater than
4.8 km, this percent declined to 22%. Forests at less than 20 km
7
from urban areas were 54% deforested. More than 80% of the
cells located less than 800 m from areas under cultivation in
1976 were deforested by 1985.
4.3.
Extrapolation of forest cover
In 1985, 46% of the study area was forested, but in 1999 this
decreased to 41% (Fig. 3). In our extrapolations, the native
forests of the study area were reduced to 38% by 2010 and
35% by 2020 (Fig. 3). This represents a loss of approximately
66,700 ha of native forest in 35 years. Although our analysis assumes that there is no regrowth of deforested areas (as
described in Section 2), there is reforestation evidence in the
satellite imagery of approximately 7% between 1976 and 1985
and 11% between 1985 and 1999.
4.4.
Observed and future trends in forest
fragmentation
For the years observed in our analysis, patch density increased
from 1.41 patches/100 ha in 1976 to 2.5 in 1999 (Fig. 4a). From
1999 to 2010, this index did not exhibit changes. However,
during the last time interval, the patch density declined to
2.2 patches/100 ha. These modifications in the configuration of
the forest cover were also associated with greater patch edge
length between forest and non-forest cover types (Fig. 4b).
The overall variation in these values indicated that the shape
Fig. 3 – Spatial and temporal patterns of forest cover in southern Chile for the years 1976, 1985, 1999, 2010, and 2020. Forest
cover maps for the years 2010 and 2020 are based on simulations that apply the annual deforestation rate between 1985
and 1999, geophysical attribute maps of slope and distance to rivers, and application of the 3 × 3 nearest neighbor rule in
GEOMOD.
ECOMOD-5004;
No. of Pages 11
8
ARTICLE IN PRESS
Fig. 4 – Changes in landscape indices applied to forest cover from 1976 to 2020. Values of indices derived from actual maps
(1976, 1985, and 1999) are depicted in solid black lines. Black-dashed lines represent extrapolated values based on the forest
loss rate between 1985 and 1999 (0.78% year−1 ). Landscape indices: (a) patch density (number of patches per 100 ha), (b) total
edge length, (c) total core area (for a distance to edge of 100 m), and (d) mean proximity index (for a distance of 1 km).
of forest patches became more irregular up to 1999. In our
simulated results total edge length of forest patches in 2020
decreased significantly (12 = 66.42, p < 0.001) (Fig. 4b) over that
of 2010. From 1976 the total core area constantly decreased
up to 1999, but for the extrapolated years, the total core area
did not appear to be significantly reduced between 1999 and
2010 (12 = 1.33, p = 0.25) and between 2010 and 2020 (12 = 0.22,
p = 0.63) (Fig. 4c). The mean proximity index, or measure of
isolation, sharply declined up to 1999. Although the index
recorded in 2010 was relatively similar to that one recorded
in 1999, a significant reduction of this index was found (12 =
2322.4, p < 0.001). Similarly, the index of proximity continued to significantly decline by 2020 (12 = 156.05, p < 0.001)
(Fig. 4d).
5.
Discussion
5.1.
Modeling approaches
GEOMOD was applied to identify the major spatial attributes
that drive landscape change as well as to simulate the progressive loss of native forest into the future. GEOMOD was able to
classify correctly 88% of grid cells of the simulated 1999 map,
recording a kappa of 0.74, which is categorized as “very good”
by Monserud and Leemans (1992). A slightly higher kappa of
0.80 was obtained using GEOMOD for land-cover change analysis in northeastern Massachusets (Pontius et al., 2003).
A strong similarity was recorded here between the two
modeling approaches used in identifying the geophysical
variables associated with forest loss. The univariate logis-
tic regression demonstrated that each explanatory variable,
excluding distance to 1976 agricultural land, yielded a high
probability of deforestation between 1985 and 1999. The
importance of these variables as drivers of deforestation was
confirmed by GEOMOD, which showed high values of kappa for
each variable, with the lowest kappa achieved using distance
to 1976 agricultural land as the independent driver. For the
same period, the multivariate logistic regression revealed that
the most significant explanatory variables (excluding patch
size and distance to patch edge that were not analyzed in GEOMOD) corresponded to those with the highest values of kappa
obtained by GEOMOD, i.e. slope and distance to rivers.
The use of logistic regression models enabled GEOMODs
results to be supplemented. For the two time intervals, the
logistic models determined that distance to patch edges was
highly significant in explaining the probability of deforestation. This is consistent with the analysis conducted using
GEOMOD, in which the simulations that produced the highest kappa were done applying the neighborhood search mode
of 3 × 3 cells. In this mode, GEOMOD constrains the selection of
cells to be deforested to those cells that are around the border
of forest patches.
Some researchers state that the difficulty in predicting the
location of deforested areas is related to the fact that they are
scattered evenly with respect to underlying factors and some
of the possibly most important variables are not available in
digital format (Schneider and Pontius, 2001). In the current
study, the deforestation processes have been concentrated in
certain sites in the landscape, which enabled significant geophysical variables to be identified. Even though most of the
variables used in this study come from the most detailed and
ECOMOD-5004;
No. of Pages 11
ARTICLE IN PRESS
9
comprehensive survey available for Chile (CONAF et al., 1999),
a number of different scales have been combined in this analysis, so that the detail required to understand a process at
the highest map scale is missing. A limitation of the study is
related to the fact that the predicted forest maps are based on
the assumption that the rate of deforestation between 1985
and 1999 will remain constant over the next decades.
Wilson et al. (2005) used logistic regression to assess the
probability of native forest conversion to industrial plantations in southern Chile. That study was limited to the
assumption that plantations were converted directly from
native forests, excluding the possibility that plantations could
have been established in previously deforested areas such as
crops, shrublands, and grasslands. In the present work, the
availability of forest covers generated at three different time
intervals enabled more complex patterns of land-use conversion to be distinguished. For each time interval, we were able
to identify those cells that were previously occupied by forests
and then converted to different land-cover types.
flood risk. These restrictions were more evident in flat areas
where the forest patches were intensely fragmented and left as
riparian vegetation. Similar results were found in Melbourne,
Australia, where the application of logistic regression to analyze the decline of native grassland revealed that patches
close to streams presented a low probability of destruction
(Williams et al., 2005).
Forested flat areas near towns and roads were highly vulnerable to native forest replacement by plantations of exotic
species in southern Chile (Wilson et al., 2005). Similarly, the
proximity to village settlements was found to be among the
most important variable of forest conversion to agricultural
land in Madagascar (McConnell et al., 2004). In contrast to
these studies, we found that distance to towns and distance to
roads were not significant in accounting for clearance of forest
area for the two time intervals examined. However, the high
values of kappa obtained by GEOMOD for these geophysical
variables show that these attributes are also important to be
able to predict the location of forested areas by 1999.
5.2.
Relating our findings to what we observe on the
ground
5.3.
Forest loss up until 1976 was most highly correlated to the
presence of volcanic ash soil, which is located in lowlands and
is the most favorable for vegetation growth (INIA, 1985), such
as agricultural crops and cattle grazing. Through our analysis we have found that between 1976 and 1999 the expansion
of crops and pasture lands continued to occur in Ñadi soil,
which is very limited in soil depth, and in gently sloping terrain
where more and more forested areas were opened for grazing
and cultivation. This process has resulted in recurrent fires,
which act as an intermediate agent of conversion from forest
to pasture lands.
In both time periods analyzed in the present study, the
clearance of forests was concentrated around edges of forest
fragments located in slightly undulating terrain. This pattern
is related to the fact that local people use trees near the borders of forest patches to produce fuelwood and then clear
these areas for crops and pasture land. Likewise, a logistic
model-based study conducted in Madagascar also found that
the expansion of agriculture into the remaining natural forest
was associated with progressive clearance from forest edges
(McConnell et al., 2004). In our study area, the spatial pattern
of forest logging during the observed years was the result of
an increase in the demand for native forest products such as
firewood and woodchips during the 1980s (Lara et al., 2002).
Currently, forest logging for firewood is the main factor driving
forest loss in the study area (Lara et al., 2002).
We found that during the first time interval, patch size was
not a significant variable due to the presence of forest fragments of different sizes that occurred in flat areas. However,
between 1985 and 1999, small patches became vulnerable to
deforestation, because they were mainly concentrated in flat
areas, where it is easier to clear forest land, thus leading to
intensification of fragmentation in these areas. Additionally,
pattern analysis revealed that the clearance of forests took
place mainly in patches located away from rivers or streams.
This finding correlates with the fact that clearance of forests
is legally prohibited in areas close to rivers or in areas with
Future trends in forest fragmentation
Based on the current trends of the geophysical variables
driving deforestation, a continuous reduction in the area of
intermediate and large fragments is expected during the next
two decades. Due to that there is evidence of reforestation
between 1976 and 1999, it is probable that the predicted areas
of native forests in 2010 and 2020 are slightly higher than our
estimates.
Because forests are continuously being affected by fragmentation over time, a decline in patch density is observed
from 2010 to 2020. This index increased in the earliest stage
of forest loss and fragmentation and then decreases during
the extrapolated years. This means that if the current trends
continue, the process of deforestation may even eliminate
forest patches created in the last decades. The identification of this threshold in the patch density has also been
reported further north in central Chile, where the decline in
patch density was recorded approximately 20 years ago due to
rapid deforestation (Echeverrı́a et al., 2006). Similarly, Zipperer
et al. (1990) observed that the constant action of deforestation led to a decline in patch density in central New York,
USA.
The native forests of our study area presented abrupt
changes in their spatial configuration over the whole study
period, from a forest habitat formed by complex clusters of
large fragments to a sparse distribution of smaller patches.
This trend of decreasing connectivity of forest fragments is the
result of increasing forest fragmentation through time, which
has dissected the native forests into more compact, isolated,
and smaller fragments. The isolation of fragments is a fundamental consequence of unchecked fragmentation and may
have negative impacts if the populations of species occurring
in these habitats have no capacity to survive in isolated fragments or to move through the surrounding modified matrix
(Willson et al., 1994; Cornelius et al., 2000; Reed and Levine,
2005; Echeverrı́a et al., 2007).
Results revealed a slight decrease of the core area and proximity of forest fragments in the next two decades. This is not
the result of a decline in the forest loss rate, but a change in
ECOMOD-5004;
No. of Pages 11
10
ARTICLE IN PRESS
the spatial configuration in which most remaining forests are
becoming more inaccessible or restricted owing to legal regulations on forest logging in steep areas and next to streams.
The study landscape in 2020 is characterized by a mosaic of
small fragments, probably influenced by edge effects, highly
isolated from large intact forests located at higher elevations.
Similarly, future projections by Pearson et al. (1999) in the
temperate forest of the USA, produced complex changes in
the spatial patterns, by increasing the number of patches and
decreasing the size of some habitats suitable for the species
studied.
6.
Conclusions
The results of our analysis demonstrate the advantages of
using standard remote sensing data along with spatially
explicit modeling approaches to identify and assess the major
geophysical variables that influence the pattern and location
of deforestation and fragmentation. Results demonstrated
that the pattern of deforestation and fragmentation may have
a notable effect on the spatial configuration of the remaining
forest fragments over the next decades and potential detrimental consequences on biodiversity conservation.
The spatial patterns described in this research reveal the
immediate drivers of deforestation and fragmentation that
operate in the study area. These drivers suggest that forest logging and clearance for crops and pasture land are the
main human activities associated with the changes in the spatial configuration of forest cover. Future studies that assess
the relationship between immediate drivers and underlying
causes of deforestation such as environmental legislation,
political economy, poverty, etc., should be conducted for a
more comprehensive understanding of the causes of forest
loss in the world.
Acknowledgements
This research was made possible by funding from BIOCORES (biodiversity conservation, restoration, and sustainable
use in fragmented forest landscapes) project ICA-CT-200110095; bursary for young researchers from developing
countries—European Union (administered by UFZ, Germany);
the UNEP-WCMC Chevening Scholarship in biodiversity; the
Frank Smart Studentship of the Department of Plant Sciences, University of Cambridge; the support from Cambridge
Commonwealth Trust & Cambridge Overseas Trust 2003-2005;
FORECOS (P04-065-F) Millennium Scientific Nucleus of MIDEPLAN; and ALFA-FOREST (contract II-0411-FA-FCD-FI-FC). CE
thanks Patricio Romero for his assistance in the preparation
of digital covers.
references
Armenteras, D., Gast, F., Villareal, H., 2003. Andean forest
fragmentation and the representativeness of protected
natural areas in the eastern Andes, Colombia. Biol. Conserv.
113, 245–256.
Asbjornsen, H., Ashton, M., Vogt, D., Palacios, S., 2004. Effects of
habitat fragmentation on the buffering capacity of edge
environments in a seasonally dry tropical oak forest
ecosystem in Oaxaca, Mexico. Agric. Ecosyst. Environ. 103,
481–495.
Bennett, A., 2003. Linkages in the Landscape. The Role of
Corridors and Connectivity in Wildlife Conservation. IUCN,
Gland, Switzerland and Cambridge, UK, 254 pp.
Bürgi, M., Hersperger, A.M., Schneeberger, N., 2004. Driving forces
of landscape change—current and new directions. Landsc.
Ecol. 19, 857–868.
Castelletta, M., Thiollay, J., Sodhi, N., 2005. The effects of extreme
forest fragmentation on the bird community of Singapore
Island. Biol. Conserv. 121, 135–155.
Chuvieco, E., 1996. Fundamentos de teledetección espacial.
Ediciones RIALP, S.A., Third ed., Madrid, Spain, 568 pp.
CONAF, CONAMA, BIRF, Universidad Austral de Chile, Pontificia
Universidad Católica de Chile, Universidad Católica de
Temuco, 1999. Catastro y Evaluación de los Recursos
Vegetacionales Nativos de Chile. Informe Nacional con
Variables Ambientales. Santiago, Chile, 88 pp.
Cornelius, C., Cofre, H., Marquet, P., 2000. Effects of habitat
fragmentation on bird species in a relict temperate forest in
semiarid Chile. Conserv. Biol. 14, 534–543.
Crawley, M., 2005. Statistical Computing. An Introduction to Data
Analysis using S-PLUS. Wiley, USA, 761 pp.
Dale, V.H., Pearson, S.M., 1997. Quantifying habitat fragmentation
due to land use change in Amazonia. In: Laurance, W.,
Bierregaard, R. (Eds.), Tropical Forest Remnants: Ecology,
Management, and Conservation of Fragmented Communities.
The University of Chicago Press, Chicago, USA,
pp. 400–414.
Dalgaard, P., 2002. Introductory Statistics with R. Springer, 267 pp.
Donoso, C., 1993. Bosques templados de Chile y Argentina:
variación, estructura y dinámica. Universitaria, Santiago,
Chile, 484 pp.
Donoso, C., Lara, A., 1997. Utilización de los bosques nativos en
Chile: pasado, presente y futuro. In: Armesto, J.J., Villagrán, C.,
Arroyo, M.K. (Eds.), Ecologı́a de los bosques nativos de Chile.
Editorial Universitaria, Santiago, Chile, pp. 335–362.
Dytham, C., 2003. Choosing and using Statistics: A Biologist’s
Guide. Blackwell Science, York, UK, pp. 218.
Echeverrı́a, C., Coomes, D., Salas, J., Rey-Benayas, J.M., Lara, A.,
Newton, A., 2006. Rapid deforestation and fragmentation of
Chilean temperate forests. Biol. Conserv. 130,
481–494.
Echeverrı́a, C., Coomes, D., Newton, A., Rey-Benayas, J.M., Lara,
A., 2007. Impacts of forest fragmentation on species
composition and forest structure in the temperate landscape
in southern Chile. Global Ecol. Biogeogr. 16, 426–439.
Evans, T., Moran, E., 2002. Spatial integration of social and
biophysical factors related to land cover change. Popul. Dev.
Rev. 28, 165–186.
Fitzsimmons, M., 2003. Effects of deforestation and reforestation
on landscape spatial structure in boreal Saskatchewan,
Canada. Forest Ecol. Manage. 174, 577–592.
Forman, R.T.T., Godron, M., 1986. Landscape Ecology. John Wiley
and Sons, USA, 619 pp.
Franklin, S., 2001. Remote Sensing for Sustainable Forest
Management. Lewis Publishers, USA, 407 pp.
Hall, C.A.S., Tian, H., Qi Y., Pontius, G., Cornell, J., Uhlig, J., 1995a.
Spatially explicit models of land use change and their
application to the tropics. DOE Research Summary, No. 31.
CDIAC, Oak Ridge National Lab.
Hall, C.A.S., Tian, H., Qi, Y., Pontius, G., Cornell, J., Uhlig, J., 1995b.
Modeling spatial and temporal patterns of tropical land use
change. J. Biogeogr. 22, 753–757.
Herrmann, H., Babbitt, K., Baber, M., Gongalton, R., 2005. Effects
of landscape characteristics on amphibian distribution in a
ECOMOD-5004;
No. of Pages 11
ARTICLE IN PRESS
forest-dominated landscape. Biol. Conserv. 123,
139–149.
Imbernon, J., Branthomme, A., 2001. Characterization of
landscape patterns of deforestation in tropical rain forests.
Inter. J. Remote Sens. 22, 1753–1765.
Instituto de Investigaciones Agropecuarias (INIA), 1985. Suelos
volcánicos de Chile. Ministerio de Agricultura, Santiago, Chile.
Janssen, I., Kruemmelbein, J., Hora, R., Ellies, A., 2004. Physical
and hydraulic properties of the Nadi soils in south
Chile—comparison between untilled and tilled soil. Revista de
la Ciencia del Suelo y Nutrición Vegetal 4, 14–28.
Lara, A., Echeverrı́a, C., Reyes, R., 2002. Bosques. In: Centro de
Análisis de Polı́ticas Públicas. Universidad de Chile (Ed.).
Informe Paı́s: Estado del Medio Ambiente en Chile-2002.
Santiago, Chile, pp. 131–160.
Laurance, W.F., 1999. Reflections on the tropical deforestation
crisis. Biol. Conserv. 91, 109–117.
Laurance, W.F., Lovejoy, T.E., Vasconcelos, H.L., Bruna, E.M.,
Didham, R.K., Stouffer, P.C., Gascon, C., Bierregaard, R.O.,
Laurance, S.G., Sampiao, E., 2002. Ecosystem decay of
Amazonian forest fragments: a 22-year investigation. Conserv.
Biol. 16, 605–618.
Martı́nez-Morales, M., 2005. Landscape patterns influencing bird
assemblages in a fragmented neotropical cloud forest. Biol.
Conserv. 121, 117–126.
McConnell, W., Sweeney, S., Mulley, B., 2004. Physical and social
access to land: spatio-temporal patterns of agricultural
expansion in Madagascar. Agriculture. Ecosyst. Environ. 101,
171–184.
Metzger, J.P., 2000. Tree functional group richness and landscape
structure in a Brazilian tropical fragmented landscape. Ecol.
Applic. 10, 1147–1161.
McGarigal, K., Cushman, S.A., Neel, M.C., Ene, E., 2002. Fragstats:
spatial pattern analysis program for categorical maps.
Retrieved January 20, 2003, from University of Massachusetts, Landscape Ecology Program web site:
http://www.umass.edu/landeco/research/fragstats/fragstats.html.
Millington, A.C., Velez-Liendo, X.M., Bradley, A.V., 2003. Scale
dependence in multitemporal mapping of forest
fragmentation in Bolivia: implications for explaining temporal
trends in landscape ecology and applications to biodiversity
conservation. J. Photogr. & Remote Sens. 57, 289–299.
Monserud, R.A., Leemans, R., 1992. Comparing global vegetation
maps with the Kappa statistic. Ecol. Model. 62, 275–293.
Myers, N., Mittermeler, R.A., Mittermeler, C.G., da Fonseca, G.A.B.,
Kent, J., 2000. Biodiversity hotspots for conservation priorities.
Nature 403, 853–858.
Pearson, S., Turner, M., Drake, J., 1999. Landscape change and
habitat availability in the southern Appalachian Highlands
and Olympic Peninsula. Ecol. Applic. 9, 1288–1304.
Pontius, R.G., 2000. Quantification error versus location error in
comparison of categorical maps. Photogr. Eng. Remote Sens.
66, 1011–1016.
Pontius, R.G., 2002. Statistical methods to partition effects of
quantity and location during comparison of categorical maps
at multiple resolutions. Photogr. Eng. Remote Sens. 68,
1041–1049.
11
Pontius, R.G., Cornell, J., Hall, C., 2001. Modelling the spatial
pattern of land-use change with GEOMOD2: application and
validation for Costa Rica. Agric. Ecosyst. Environ. 85, 191–203.
Pontius, R.G., Agrawal, A., Huffaker, D., 2003. Estimating the
uncertainty of land-cover extrapolations while constructing a
raster map from tabular data. J. Geogr. Syst. 5, 253–273.
Porej, D., Micacchion, M., Hetherington, T.E., 2004. Core terrestrial
habitat for conservation of local populations of salamanders
and wood frogs in agricultural landscapes. Biol. Conserv. 120,
399–409.
Reed, R., Johnson-Barnard, J., Baker, W., 1996. Fragmentation of a
forested rocky mountain landscape, 1950–1993. Biol. Conserv.
75, 267–277.
Reed, M., Levine, S., 2005. A model for behavioral regulation of
metapopulation dynamics. Ecol. Model. 183, 411–423.
Reyes, R., 2000. Caracterización de los sistemas de producción y
comercialización de leña para la ciudad de Puerto Montt, X
Región. Thesis, Facultad de Ciencias Forestales, Universidad
de Chile, Santiago, Chile.
Saunders, D.A., Hobbs, R.J., Margules, C.R., 1991. Biological
consequences of ecosystem, fragmentation: a review. Conserv.
Biol. 5, 18–32.
Schlatter, J., Gerding, V., Huber, H., 1995. Sistema de
Ordenamiento de la Tierra. Herramienta para la planificación
forestal aplicado a la X Región. Serie Técnica. Facultad de
Ciencias Forestales. Universidad Austral de Chile, Valdivia.
Schneider, L., Pontius, R.G., 2001. Modeling land-use change in
the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst.
Environ. 85, 83–94.
Serneels, S., Lambin, E., 2001. Proximate causes of land-cover
change in Narok District, Kenya: a spatial statistical model.
Agric. Ecosyst. Environ. 85, 65–81.
Staus, N., Strittholt, J., Dellasala, D., Robinson, R., 2002. Rate and
patterns of forest disturbance in the Klamath-Siskiyou
ecoregion, USA between 1972 and 1992. Landsc. Ecol. 17,
455–470.
Turner, M.G., Gardner, R.H., O’Neill, R.V., 2001. Landscape Ecology
in Theory and Practice: Pattern and Process. Springer, New
York, 497 pp.
Vergara, P., 2005. Predation on bird nests in forest edges of a
National Reserve of the Coastal Range of the Maule Region. In:
Smith-Ramirez, C., Armesto, J.J., Valdovinos, C. (Eds.), Historia,
biodiversidad y ecologiı̌a de los bosques costeros de Chile.
Editorial Universitaria, Santiago, Chile, pp. 578–585.
Williams, N.G., McDonnell, M.J., Seager, E., 2005. Factors
influencing the loss of an endangered ecosystem in an
urbanizing landscape: a case study of native grasslands from
Melbourne, Australia. Landsc. Urban Plan. 71, 35–49.
Willson, M., De Santo, T.I., Sabag, C., Armesto, J.J., 1994. Avian
communities of fragmented south-temperate rainforests in
Chile. Conserv. Biol. 8, 508–520.
Wilson, K., Newton, A., Echeverrı́a, C., Weston, C., Burgman, M.,
2005. A vulnerability analysis of the temperate forests of
south central Chile. Biol. Conserv. 122, 9–21.
Zipperer, W.C., Burgess, R.L., Nyland, R.D., 1990. Patterns of
deforestation and reforestation in different landscape types
in central New York. Forest Ecol. Manage. 36, 103–117.

article in press - CamTools

Transcription

Similar documents

champneys - Bouygues UK

SUSTAINABLE PACIFIC GROVE APRIL MEETING

Parque Nacional Natural Cueva de Los Guacharos

Some facts about Biggest Roulette Win In Vegas

Folie 1

“LUCIAN GRIGORESCU” SCHOOL MEDGIDIA – CONSTANTA

Trails and Town / State Owned Lands

Website: www.forru.org