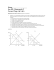Pricing II: Constant Elasticity

Pricing II: Constant Elasticity
This module covers the relationships between price and
quantity, elastic demand, inelastic demand, and optimal
price under conditions of constant elasticity.
Authors: Paul Farris and Phil Pfeifer
Marketing Metrics Reference: Chapter 7
© 2010-14 Paul Farris, Phil Pfeifer and Management by the Numbers, Inc.
People use elasticity loosely to mean how responsive is demand to
changes in price:
• Elastic demand means quantity is very responsive.
• Inelastic demand is when quantity does not decrease (much) when
the price increases (and vice versa).
PRICE ELASTICITY
Price Elasticity
At this level, most of us know what elasticity means. The challenge
comes when we try to measure elasticity or responsiveness.
The formal definition of elasticity has two important parts:
• The unit change in quantity per small unit change in price (the slope)
and
• The reference point for measuring those unit changes as percentage
changes.
As we saw in Pricing I, linear functions have constant slope and a
different elasticity at each price point.
MBTN | Management by the Numbers
2
Unlike linear functions, constant
elasticity functions exhibit a different
slope, but the same elasticity at
each point on the curve. This
means the slope is changing at a very
specific rate to keep elasticity
constant.
A mathematical equation for this
relationships is Q = kP℮ where e is the
price elasticity of demand and k is a
constant.* For constant elasticity
functions we can use the elasticity to
find the profit-maximizing price. If we
know cost and elasticity, there are
only two steps required.
*k is the quantity the firm would
sell at a price = $1.
Definition
CONSTANT ELASTICITY PRICE-QUANTITY FUNCTIONS
Constant Elasticity Price-Quantity Functions
Under conditions of constant elasticity, Q = kP℮ and k = Q / P℮
MBTN | Management by the Numbers
3
To calculate the optimal price using cost and
elasticity there are two steps:
1. Calculate the absolute value of the
reciprocal of elasticity. The resulting
number tells us what margin is optimal
(and, by extension, what price is
optimal). For example, a -2 elasticity
would result in an optimal margin of
50%., a -4 elasticity would result in an
optimal margin of 25%, and so on.
2. Use cost and the optimal margin to
calculate the optimal price = Cost / (1Margin). For a cost of $0.75 per unit and
an elasticity of -2, the profit-maximizing
price would be $0.75 / (1 - .5) = $1.50.
CONSTANT ELASTICITY FUNCTIONS
Constant Elasticity Price-Quantity Functions
Definition
With constant elasticity, Optimal margin = ABS (1 / elasticity)
MBTN | Management by the Numbers
4
Question 1
EXERCISE 1
Exercise 1
For a constant elasticity function with an elasticity of -4 and a
unit cost of $2.00, what is the profit-maximizing price?
Answer:
Step 1: Optimal Margin = absolute value of (1 / -4) = 25%
Step 2: Optimal Price = $2.00 / (1 - .25) = $2.67
MBTN | Management by the Numbers
5
The more “elastic” the curve,
the greater the % change in quantity
for a given % change in price.
Compare the curve with the -4
elasticity with the curve with a -2
elasticity (displayed at right).
Higher elasticity mean lower optimal
margins. The more “responsive” is
demand, the more aggressive the
firm should be in its pricing.
Note: As we saw in the last section, at the
optimal price, elasticity is always greater than
1 (or less than -1, depending on how you like to
think about it). Margin can never be more than
100%!! And if it is less than 0%, you have
bigger pricing problems than finding the optimal.
MBTN | Management by the Numbers
HIGHER ELASTICITY MEANS LOWER MARGINS
Higher Elasticity Means Lower Margins
6
Cost
$1.25
Price
Quantity $Margin %Margin Profit
$1.00
500.00
-0.25
-25% -125.00
$1.10
341.51
-0.15
-14%
-51.23
$1.20
241.13
-0.05
-4%
-12.06
$1.30
175.06
0.05
4%
8.75
$1.40
130.15
0.15
11%
19.52
$1.50
98.77
0.25
17%
24.69
$1.60
76.29
0.35
22%
26.70
$1.70
59.87
0.45
26%
26.94
$1.80
47.63
0.55
31%
26.20
$1.90
38.37
0.65
34%
24.94
$2.00
31.25
0.75
38%
23.44
$2.10
25.71
0.85
40%
21.85
$2.20
21.34
0.95
43%
20.28
$2.30
17.87
1.05
46%
18.76
$2.40
15.07
1.15
48%
17.33
$1.67
64.28
0.42
25%
27.00
Note: Profitmaximizing price
occurs at 25% margin
= 1 / (-4)
Q = 500*P-4
SPREADSHEET CALCULATION
Spreadsheet Calculation of Profit-Maximizing Price
Insight
If your percentage
margin is less than 1 /
elasticity, you should
seriously consider
raising your price.
Profit Maximizing
Price
7
If you are only given two observations of price and quantity, it is
impossible to say whether the best function to use is linear or constant
elasticity. For example, if a business determined the following:
Price
$10
$15
Quantity
100
50
If demand is linear: slope = 50 / 5 = 10 and MRP = 20.
For a cost of $5, the optimal price would be:
½ * (Cost + MRP) = ½ * (5 + 20) = $12.50
For constant elasticity demand, elasticity is calculated using Excel or
a scientific calculator as ln (50 / 100) / ln (15 / 10) = -1.71.
The optimal margin would be 1 / 1.71 = 58.5% and the optimal price
would be cost / (1 - margin) = $5 / (1 - .585) = $12.05
WORKING BACKWARDS FROM OBSERVATIONS
Calculating Profit-Maximizing Price
Note: ln = natural log. So, ln(.5) would be read as natural log of .5
MBTN | Management by the Numbers
8
For constant elasticity demand functions you will need to use Excel or a
scientific calculator to predict unit sales resulting from a new unit price.
The formula is: Q = K*Pe.
Q = K*Pe where e is the price elasticity of demand and K is a constant
Question 2: With two points of price and quantity, the elasticity is
estimated by calculating ln (Q2 / Q1) / ln (P2 / P1), but how do you find
K?
Answer:
Use either Q2 and P2 or Q1 and P1 in the equation. For example, using
quantity of 100 and price of $10 from the previous example and the
elasticity of -1.71, we have 100 = K * 10 ^ -1.71.
100 =K*.0195, K = 5,128.
PREDICTING SALES FOR CONSTANT ELASTICTY
Predicting Sales for Constant Elasticity
To “predict” sales at a price of $15, Q= 5,128 * 15 ^ -1.71 = 50.
MBTN | Management by the Numbers
9
Marketing Metrics by Farris, Bendle, Pfeifer and
Reibstein, 2nd edition, chapter 7.
- And the following MBTN modules -
FURTHER REFERENCE
Further Reference
Pricing I: Linear Demand - This module explores pricing
under the assumption of demand curves that are not linear.
Profit Dynamics - This module is a more basic module
that examines price-volume trade-offs.
Promotion Profitability - This module examines the role
of promotion in pricing decisions.
MBTN | Management by the Numbers
10