Document 6564469

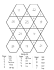
Geometry Notes G.6 SSS, SAS, HL
Mrs. Grieser
Name: _________________________________________ Date: _________________ Block: __________
Prove Triangles Congruent by SSS
Side-Side-Side (SSS) Congruence Postulate
If three sides of one triangle are congruent to three sides of
a second triangle, then the two triangles are congruent.
Example 1: Prove triangle congruence using SSS
Given: AB  CD, AD  CB
Prove: ABD  CBD
Statements
1) AB  CD, AD  CB
2) BD  BD
3) ABD  CDB
Reasons
1) Given
2)_____________________________
3) SSS Congruence Postulate
Example 2: Triangle congruence in a coordinate plane
Using the coordinate plane at right, prove ABC  CDE .

Find the lengths of each side using the distance formula:
(x1  x2 )2  (y1  y 2 )2
d=
AB =
CD =
BC =
DE =
AC =
CE =

Are the triangles congruent? _______ Why or why not? ___________
You try... Decide whether the triangles are congruent, explaining your reasoning:
a)
WXY  WZY
d) PQR  RTS
b) RST  VUT
c) FGH  JHG
e) JKL  MPN
f) ABC  DEF
Geometry Notes G.6 SSS, SAS, HL
Mrs. Grieser Page 2
Prove Triangles Congruent by SAS and HL
Side-Angle-Side (SAS) Congruence Postulate
If two sides and the included angle of one triangle are
congruent to two sides and the included angle of a second
triangle, then the two triangles are congruent.
SSA is NOT enough to prove congruence (we can possibly get two triangles).
However, if the angle in SSA is a right angle, we CAN prove congruence.

Hypotenuse: side opposite the right angle in a right triangle

Leg: side adjacent (next to) the right angle in a right triangle
Hypotenuse-Leg (HL) Congruence Theorem
If the hypotenuse and a leg of a right triangle are congruent
to the hypotenuse and a leg of a second right triangle, then
the two triangles are congruent.
Example 3: SAS
Given: BC  DA, BC||AD
Prove: ABC  CDA
Statements
Example 4: HL
Given: WY  XZ, WZ  ZY,XY  ZY
Prove: WZY  XYZ
Statements
Reasons
1) Given
1) WY  XZ, WZ  ZY,
1) BC  DA, BC||AD
Reasons
1) Given
2) BCA  DAC
2)___________________
3) AC  AC
3) __________________
4) ABC  CDA
4) SAS
XY  ZY
2) WZY , XYZ are
rt. angles
2)___________________
3) WZY , XYZ are
rt. ∆s
3) __________________
4) ZY  YZ
4) __________________
5) WZY  XYZ
5) HL
You try... Decide whether the triangles are congruent, explaining your reasoning
a) PQT  RQS
b) NKJ  LKM
c) WXY  ZXY
d) MRS  MPQ
e) ABC  DBC
f) JKL  MLK , given
JK  ML