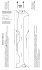Tugas Analisa Numerik

Tugas Analisa Numerik
Tugas dikumpulkan dalam format pdf dengan penamaan file : tugas_anum_NRP.pdf
Batas akhir pengumpulan tugas : 1 Juni 2015 jam 15:00 WIB
Dikirim ke alamat email : unggul@me.its.ac.id
1. If the velocity distribution of a fluid flowing through a pipe is known (Fig. 1), the flow rate
Q (that
´ is, the volume of water passing through the pipe per unit time) can be computed by
Q = vdA. where v is the velocity and A is the pipe’s crosssectional area. (To grasp the
meaning of this relationship physically, recall the close connection between summation and
integration.) For a circular pipe, A = πr2 and dA = 2πr dr. Therefore
ˆ r
v (2πr) dr
Q=
0
where r is the radial distance measured outward from the center of the pipe. If the velocity
distribution is given by
1
r 6
v = 2 1−
r0
where r0 is the total radius, If the total radius is based on your last number of NRP in cm (10 for
the case last number is 0) compute Q using the multiple-application trapezoidal rule. Discuss
the results.
Figure 1:
2. The basic differential equation of the elastic curve for a cantilever beam (Fig. 2) is given as
d2y
= −P (L − x)
dt 2
where E is the modulus of elasticity and I is the moment of inertia. Solve for the deflection of
the beam using Heun’s method and Third-Order Runge-Kutta method. The following parameter
values apply: E = 30000 ksi, I = 800 in4 , P = 1 kip, L = 10 f t. Compare your numerical results
to the analytical solution,
PLx2 Px3
+
y=−
2EI
6EI
EI
Figure 2:
1