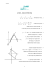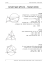) ` ח כיתה – למדא / " בריבוע עשר "(

‫‪.11‬‬
‫("עשר בריבוע" ‪ /‬למדא – כיתה ח' )‬
‫‪.11‬‬
‫‪1‬‬
‫("עשר בריבוע" ‪ /‬למדא – כיתה ח' )‬
‫גיאומטריה של המישור‬
‫‪.1‬‬
‫("עשר בריבוע" ‪ /‬למדא – כיתה ח' )‬
‫‪.1‬‬
‫("עשר בריבוע" ‪ /‬למדא – כיתה ח' )‬
‫‪.3‬‬
‫(עוזרי ושלו – ט' חלק א'‪)11 / 182 :‬‬
‫‪2‬‬
‫‪.2‬‬
‫נתון ‪ LGKC‬מלבן‪ .‬הנקודה ‪ M‬היא אמצע הצלע ‪.CK‬‬
‫‪L‬‬
‫‪G‬‬
‫‪E‬‬
‫‪.EK  GM,RC  LM‬‬
‫א‪ .‬הוכיחו‪.∆LCM ≅∆GKM :‬‬
‫‪K‬‬
‫ב‪ .‬הוכיחו‪.∆CRM ≅∆KEM :‬‬
‫‪R‬‬
‫‪M‬‬
‫ג‪ .‬מצא בסרטוט לפחות שני משולשים שדומים למשולש ‪ .∆EGK‬רשמו אותם ונמקו את צעדיכם‪.‬‬
‫ד‪ .‬הוכיחו‪( .REIICK :‬רמז‪ :‬מהו סוג המשולש ‪)?∆REM‬‬
‫("אפשר גם אחרת" – ט' (אפור) – חלק א'‪)1/ 123 :‬‬
‫‪.1‬‬
‫‪ PEN‬משולש ישר זווית ושווה שוקיים‪.)∡H = 90( .‬‬
‫‪ ET‬חוצה הזווית הישרה‪.‬‬
‫דרך הנקודה ‪ S‬שעל היתר העבירו מקביל לניצב ‪.NE‬‬
‫הוכיחו כי ‪ SHEN‬טרפז שווה שוקיים‪.‬‬
‫‪.7‬‬
‫("אפשר גם אחרת" – ט' (אפור) – חלק א'‪)11/ 122 :‬‬
‫‪.1‬‬
‫("שבילים" – כיתה ט' – חלק ‪)12 / 181 ,1‬‬
‫‪3‬‬
‫‪C‬‬
‫‪.7‬‬
‫("משבצת" – כיתה ט' ‪)12/ 113 ,‬‬
‫‪.8‬‬
‫‪ EF , DE‬קטעי אמצעים במשולש ‪.ABC‬‬
‫א‪ .‬אילו מהטענות הבאות נכונות תמיד?‬
‫‪EG = DG .I‬‬
‫‪ BF .II‬תיכון לצלע ‪AC‬‬
‫‪FD  AB .III‬‬
‫‪2  GE = FC .IV‬‬
‫ב‪ .‬בחרו אחת מהטענות שבחרתם בסעיף א' כנכונות והוכיחו‬
‫אותה‪.‬‬
‫‪A‬‬
‫‪B‬‬
‫‪E‬‬
‫‪ .12‬במעוין ‪ABCD‬‬
‫‪O‬‬
‫‪ BE‬ו – ‪ DF‬חוצים בהתאמה את‬
‫‪F‬‬
‫‪4‬‬
‫‪C‬‬
‫‪D‬‬
‫הזויות ‪ ABD‬ו‪CDO -‬‬
‫הוכח כי המרובע ‪ BEDF‬הוא מעוין‪.‬‬
‫‪ .01‬בריבוע ‪ ABCD‬הנקדות ‪ E‬ו – ‪ F‬נמצאות על הצלעות‬
‫‪ BC‬ו ‪ CD -‬בהתאמה‪.‬‬
‫נתון‪BF=AE :‬‬
‫‪A‬‬
‫‪B‬‬
‫א‪ .‬הוכח כי ‪BAE  CBF‬‬
‫ב‪ .‬הוכח ‪. AE  BF‬‬
‫‪E‬‬
‫‪C‬‬
‫‪D‬‬
‫‪F‬‬
‫‪A‬‬
‫‪ .11‬הקטע ‪ AD‬הוא תיכון לצלע ‪ BC‬במשולש ‪.ABC‬‬
‫‪ DE‬חוצה את הזוית ‪ ADC‬ומאונך לצלע ‪.AC‬‬
‫הוכח כי המשולש ‪ ABC‬הוא משולש ישר זוית‪.‬‬
‫‪E‬‬
‫‪B‬‬
‫‪C‬‬
‫‪D‬‬
‫‪ .11‬מרובע ‪ ABCD‬הוא מקבילית‪ O .‬נקודת מפגש‬
‫‪B‬‬
‫האלכסונים‪ KE .‬קטע העובר דרך ‪ O‬והמחבר‬
‫‪A‬‬
‫‪K‬‬
‫את הצלעות הנגדיות‪.‬‬
‫נתון‪:‬‬
‫‪ 13‬ס"מ =‪,AK‬‬
‫‪ 17‬ס"מ = ‪,DE‬‬
‫‪DAC  90‬‬
‫‪O‬‬
‫‪DCA  30‬‬
‫‪C‬‬
‫חשב את היקף המקבילית‪.‬‬
‫‪D‬‬
‫‪E‬‬
‫‪N‬‬
‫‪.13‬‬
‫‪ ABCD‬מקבילית‪ CN .‬חוצה זוית ‪.C‬‬
‫‪A‬‬
‫‪B‬‬
‫על המשך ‪ CD‬מקצים ‪.DE=AD‬‬
‫הוכח‪ENC  90 :‬‬
‫‪C‬‬
‫‪5‬‬
‫‪D‬‬
‫‪E‬‬
‫‪ .12‬מרובע ‪ ABCD‬הוא מקבילית‪.‬‬
‫‪B‬‬
‫‪E‬‬
‫‪F‬‬
‫‪ O‬נקודת מפגש האלכסונים‪.‬‬
‫‪O‬‬
‫הנקודות ‪ G ,F ,E‬ו – ‪ H‬הן אמצעי‬
‫הקטעים‪ ,CO ,BO ,AO :‬ו – ‪ DO‬בהתאמה‪.‬‬
‫זווית ‪DAB‬‬
‫‪H‬‬
‫‪G‬‬
‫הוכח‪ :‬מרובע ‪ EFGH‬מקבילית‪.‬‬
‫‪ .11‬מרובע ‪ ABCD‬הוא מקבילית‪ AE .‬חוצה‬
‫‪A‬‬
‫‪C‬‬
‫‪E‬‬
‫‪b‬‬
‫‪C‬‬
‫‪D‬‬
‫‪D‬‬
‫‪a‬‬
‫נתון‪ EC=b :‬ו ‪.DE=a -‬‬
‫הוכח כי היקף המקבילית שווה ל ‪.4a+2b‬‬
‫‪E‬‬
‫‪B‬‬
‫‪ .11‬מרובע ‪ ABCD‬הוא מלבן‪.EB=AE .‬‬
‫‪B‬‬
‫‪A‬‬
‫‪N‬‬
‫‪K‬‬
‫‪A‬‬
‫הוכח‪:‬‬
‫א‪EC=ED .‬‬
‫ב‪KB=AN .‬‬
‫ג‪ .‬נתון ‪ DEC  60‬הוכח כי‬
‫‪D‬‬
‫‪C‬‬
‫המשולש ‪ ENK‬הוא שווה צלעות‪.‬‬
‫‪A‬‬
‫‪ .17‬במשולש ‪ ABC‬הקטע ‪ BD‬הוא חוצה זווית ‪.B‬‬
‫‪E‬‬
‫הנקודה ‪ E‬נמצאת על המשכו של ‪BD‬‬
‫‪G‬‬
‫‪D‬‬
‫‪ EG BC‬ו ‪EF AB -‬‬
‫הוכח כי ‪. GF  BE‬‬
‫‪C‬‬
‫‪ M .18‬היא נקודת מפגש האלכסונים במעוין ‪.ABCD‬‬
‫נתון‪ AE BD :‬ו ‪-‬‬
‫‪B‬‬
‫‪F‬‬
‫‪D‬‬
‫‪C‬‬
‫‪ED AC‬‬
‫‪M‬‬
‫‪K‬‬
‫‪E‬‬
‫‪6‬‬
‫‪B‬‬
‫‪A‬‬
‫‪B‬‬
‫‪C‬‬
‫א‪ .‬הוכח מרובע ‪ MAED‬הוא מלבן‪.‬‬
‫ב‪ .‬הוכח ‪AB=2MK‬‬
‫( ‪ K‬היא נקודת מפגש האלכסונים ‪ AD‬ו‪)EM -‬‬
‫‪D‬‬
‫‪E‬‬
‫‪F‬‬
‫‪A‬‬
‫‪B‬‬
‫‪K‬‬
‫‪ .12‬מרובע ‪ ABCD‬הוא טרפז‪ EF .‬קטע אמצעים בטרפז‪.‬‬
‫‪ BK‬ו ‪ AC -‬נפגשים בנקודה ‪ N‬הנמצאת על ‪EF‬‬
‫‪F‬‬
‫א‪ .‬הוכח כי מרובע ‪ ABCK‬מקבילית‪.‬‬
‫‪A‬‬
‫‪N‬‬
‫‪M‬‬
‫‪E‬‬
‫ב‪ .‬נתון‪7 :‬ס"מ=‪11 , EN‬ס"מ= ‪EF‬‬
‫חשב את אורך בסיסי הטרפז‬
‫‪C‬‬
‫‪D‬‬
‫‪K‬‬
‫‪ CD‬ו‪ AB -‬ואת אורך הקטע ‪.EM‬‬
‫‪ .12‬במקבילית ‪ ABCD‬נתון‪:‬‬
‫‪FK CD DE=FE‬‬
‫הוכח‪AK=BF :‬‬
‫‪A‬‬
‫‪ DE .11‬קטע אמצעים במשולש ‪.ABC‬‬
‫הנקודה ‪ F‬נמצאת על ‪DE‬‬
‫‪E‬‬
‫‪F‬‬
‫‪D‬‬
‫כך שזווית ‪ AFB‬היא זווית ישרה‪.‬‬
‫הוכח‪ BF :‬חוצה זווית ‪.B‬‬
‫‪C‬‬
‫‪7‬‬
‫‪B‬‬
8