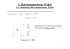Stehende Welle im Dipol
Transcription
Stehende Welle im Dipol
V Eletromagnetische Wellen 18. Elektrische Dipolschwingungen Induktive Kopplung eines Stabdipol mit einem angeregten Schwingkreis Um einen Stabdipol zum Schwingen zu bringen benötigt man hohe Frequenzen, da der Stabdipol ca. 0,3m lang ist. Ein Dipol schwingt immer in der Grundschwingung, d.h. Länge= 0.3m= λ/2 → c=f·λ f= c/λ = 3,0 108m/s / 0,6 m = 500 M Hz Um eine Schwigung am Dipol zu erreichen benötigt man einen Erregerschwingkreis mit sehr hohen Frequenzen. Diese hohen Frequenzen erreicht man dadurch, dass man die Induktivität und die Kapazität des Schwingkreises verkleinert, da: f= 1/ 2π√L·C Mechanisch wird dies dadurch erreicht, dass man die Spule des Schwingkreises auf eine Schleife reduziert. Induktiv ist diese Kopplung, da die Schwingung durch Veränderungen am Magnetfeld erzeugt wird. Stromstärke- und Ladungsverteilung längs eines Dipols Befestigt man Glühlämpchen am Dipol stellt man fest, dass sie je heller leuchten je näher sie an der Mitte des Stabdipols befestigt werden. Um die Ladungsverteilung zu überprüfen führt man eine einseitig geerdete Glimmlampe an ihm entlang. Man bemerkt, dass die Lampe an den Dipolenden stark leuchtet gegen Mitte hin dagegen erlischt. Stehende Welle im Dipol Die Eigenschwingung des Dipols läst sich als stehende Welle deuten: Betrachtet man die Stromstärkeverteilung längs eines Dipols, so stellt man fest, dass sie sich wie die Auslenkung der Seilteilchen bei einer stehenden Seilwelle verhält. Solch einen Dipol bezeichnet man in der Grundschwingung als λ/2 – Dipol, weil seine Länge der halben Wellenlänge der zugehörigen fortschreitenden Welle entspricht. Außerdem wird er auch Hertz`scher Dipol genannt, da der deutsche Physiker Heinrich Rudolph Hertz (1857- 1894) im Jahre 1886 als Erster elektromagnetische Wellen mit Dipolen erzeugte und nachwies. Schwingungen am Dipol: Grundschwingung: l = λ/2 t = 0 ; T/2 ; usw. 1 Oberschwingung: l = λ t = T/4 ; 5/4 T ; usw. 2 Oberschwingung l = 3/2 λ t = ¾ T ; 7/4 T ; usw. l = Länge T = Periodendauer Die Ausbreitungsgeschwindigkeit einer Elektromagnetischen Welle bei Vakuum ist die Lichtgeschwindigkeit c . c = 3,00 • 108 m/s Sie kann durch die Formel c = λ • f = λ/T berechnet werden. λ = Wellenlänge f = Frequenz T = Periodendauer Aufgaben BS 136 1-2 : 1 Ein Dipol schwingt in der Grundschwingung; er ist 80 cm lang. a) Wie groß ist ihre Frequenz? b) Wie groß wäre die Frequenz, wenn die erste Oberschwingung des Dipols angeregt würde? Zu a) f = c/2λ = 3,00 • 108 m/s / 2 • 0,8 m = 1,9 • 108 Hz Zu b) f = c/λ = 3,00 • 108 m/s / 0,8 m = 3,8 • 108 Hz 2 Ein 50 cm langer Dipol schwingt in der Grundschwingung. Welche Größe hat das Produkt aus Kapazität und Induktivität des Dipols? f = c/ 2λ f = 1 / 2π(LC)2 c/2λ = 1 / 2π(LC)2 ⇒ LC = (λ/cπ)2 = (0,5m / 3,00 • 108 m/s • π)2 = 2,8 • 10-19 s²