Heft 168 Wei Yang Discrete-Continuous Downscaling Model for

Transcription

Heft 168
Wei Yang
Discrete-Continuous Downscaling
Model for Generating Daily
Precipitation Time Series
Discrete-Continuous Downscaling Model for Generating
Daily Precipitation Time Series
Von der Fakultät Bau- und Umweltingenieurwissenschaften der
Universität Stuttgart zur Erlangung der Würde eines
Doktor-Ingenieurs (Dr.-Ing.) genehmigte Abhandlung
Vorgelegt von
Wei Yang
aus Shanghai, China
Hauptberichter:
Mitberichter:
Prof. Dr. rer. nat. Dr.-Ing. András Bárdossy
Prof. Dr. Hans von Storch
Tag der mündlichen Prüfung:
25. Oktober 2007
Institut für Wasserbau der Universität Stuttgart
2008
Heft 168
Discrete-Continuous Downscaling Model for Generating
Daily Precipitation Time Series
von
Dr.-Ing.
Wei Yang
Eigenverlag des Instituts für Wasserbau der Universität Stuttgart
D93
Discrete-Continuous Downscaling Model for Generating Daily
Precipitation Time Series
Titelaufnahme der Deutschen Bibliothek
Yang, Wei:
Discrete-Continuous Downscaling Model for Generating Daily Precipitation Time
Series / von Wei Yang. Institut für Wasserbau, Universität Stuttgart.
Stuttgart: Inst. für Wasserbau, 2008
(Mitteilungen / Institut für Wasserbau, Universität Stuttgart: H. 168)
Zugl.: Stuttgart, Univ., Diss., 2008)
ISBN 3-933761-72-7
NE: Institut für Wasserbau <Stuttgart>: Mitteilungen
Gegen Vervielfältigung und Übersetzung bestehen keine Einwände, es wird lediglich
um Quellenangabe gebeten.
Herausgegeben 2008 vom Eigenverlag des Instituts für Wasserbau
Druck: Document Center S. Kästl, Ostfildern
Acknowledgement
This doctoral work was done within two EU-supported projects: Statistical and Regional dynamical Downscaling of Extremes for European regions(STARDEX), supported by the European Commission under the Fifth Framework Program and contributing to the implementation
of the Key Action “Global change, climate and biodiversity ”within the Environment, Energy
and Sustainable Development, and a Regional Model for Integrated Water Management in
Twinned River Basins (RIVERTWIN), supported by the European Commission under the
Sixth framework program.
First of all, I would like to thank Prof. Dr. rer. nat. Dr.-Ing. habil. András Bárdossy for
guiding me into this interdisciplinary field. His profound knowledge and expertise in research
fields always lead me to a proper direction when I was at the crossroads. Without his encouragement, effort and advices, this work would not have been realized. I would like to also
express my gratitude to Prof. Hans von Storch, who is willing to co-supervise my work and
always gives any supports when I needed. I would like to take this opportunity to thank Prof.
Hans Caspary for his continuous support and valuable discussions.
I would like to express my gratitude to all the members of the Chair of Hydrology and
Geohydrology. It is a pleasant working group, where I could have fruitful discussions about
topics with Jan Bliefernicht, Yeshewatesfa Hundecha, Li Jing, Fredrik Wetterhall. It is a
pleasure for me to work together with Jens Götzinger for his cooperations in the project works
and his help in writing the German version of the summary of my work. I am also indebted to
Ms. Maureen Lynch for all the time she spent for proofreading of my manuscripts. I would like
to thank other friends like Jürgen Brommundt, Christian Ebert, Arne Färber, Abror Gafurov,
Wei Hu, Johanna Jagelke, Krista Uhrmann, who were always there to give me the helps.
Finally, I am extremely grateful to my beloved family, my parents PinWei Yang and Xianglin
Kong, my brother Jie Yang and my husband Zhengmin Fang, who have provided moral supports
during my studies.
i
Contents
Acknowledgement
i
List of Figures
v
List of Tables
x
Abbreviation and Acronym
xiii
Abstract
xv
Zusammenfassung
xvii
0.1
Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xvii
0.2
Methodik und Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . xviii
0.3
Diskussion und Schlussfolgerungen . . . . . . . . . . . . . . . . . . . . . . . . .
1 Introduction
1.1
xx
1
Problem and motivation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1.1
Hydro-meteorology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1.2
Global warming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2
Need for downscaling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.3
Objectives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2 Downscaling approaches
9
2.1
Dynamical downscaling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.2
Statistical downscaling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
2.2.1
Analog approaches . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
2.2.2
Circulation pattern (CP) based approaches . . . . . . . . . . . . . . . .
16
2.2.3
Regression approaches . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
2.2.4
Weather Generator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
3 Development of a new circulation-pattern-based downscaling scheme
3.1
Fuzzy-rule based classification scheme . . . . . . . . . . . . . . . . . . . . . . .
ii
21
21
Contents
3.1.1
Methodology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
3.1.2
Consistency analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
3.2
Coupling atmospheric moisture flux
. . . . . . . . . . . . . . . . . . . . . . . .
25
3.3
Conditional multivariate downscaling approach . . . . . . . . . . . . . . . . . .
26
3.3.1
Precipitation occurrence model . . . . . . . . . . . . . . . . . . . . . . .
26
3.3.2
Precipitation amount model . . . . . . . . . . . . . . . . . . . . . . . . .
27
3.3.3
Spatial variability of rainfall events . . . . . . . . . . . . . . . . . . . . .
31
3.3.4
Parameter estimation . . . . . . . . . . . . . . . . . . . . . . . . . . . .
33
Application to climate change studies . . . . . . . . . . . . . . . . . . . . . . .
36
3.4.1
IPCC scenarios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
3.4.2
Climate scenarios for application . . . . . . . . . . . . . . . . . . . . . .
37
Evaluation procedure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
3.5.1
Evaluation for CP classification . . . . . . . . . . . . . . . . . . . . . . .
40
3.5.2
Evaluation of model performance . . . . . . . . . . . . . . . . . . . . . .
44
3.4
3.5
4 Application of the CP- and Regression-based rainfall model
4.1
4.2
45
Application in the Neckar River basin . . . . . . . . . . . . . . . . . . . . . . .
45
4.1.1
Study area . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
4.1.2
CP Classification . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.1.3
Identification of a dominant atmospheric moisture flux . . . . . . . . . .
56
4.1.4
Determination of rainfall probability . . . . . . . . . . . . . . . . . . . .
58
4.1.5
60
4.1.6
Climate scenarios . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
67
Application in the Chirchik-Ahangran River Basin . . . . . . . . . . . . . . . .
70
4.2.1
Study area . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
70
4.2.2
Identification of circulation patterns . . . . . . . . . . . . . . . . . . . .
74
4.2.3
Identification of atmospheric moisture flux on rainfall . . . . . . . . . .
79
4.2.4
Determination of rainfall probability . . . . . . . . . . . . . . . . . . . .
79
4.2.5
81
4.2.6
85
5 Development of a multiple-site weather generator
91
5.1
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
5.2
Application of a weather generator in Ouémé Basin in western Africa . . . . . .
91
5.2.1
Study area . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
5.2.2
Multi-site weather generator
. . . . . . . . . . . . . . . . . . . . . . . .
93
5.2.3
Evaluation of the model’s performance . . . . . . . . . . . . . . . . . . .
95
iii
Contents
5.2.4
6 Development of a multivariate downscaling model using copulas
97
105
6.1
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
6.2
Basics of copula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
6.3
Application of copula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
6.3.1
Empirical copula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107
6.3.2
Theoretical copula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
6.3.3
Parameter estimation and rainfall generation . . . . . . . . . . . . . . . 115
6.3.4
Model performance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
7 Conclusion and further development
7.1
7.2
125
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125
7.1.1
CP- and regression-based downscaling model . . . . . . . . . . . . . . . 125
7.1.2
Weather generator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
Further development . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
iv
List of Figures
1.1
Circulation of water around, over and through the Earth (USGS 1973). . . . .
2
1.2
Water budget amongst atmosphere, land and ocean (Peixoto and Kettani, 1973).
3
1.3
Variation of the Earth’s surface temperature (IPCC Working Group I). . . . .
5
1.4
Impact of Climate Change (IPCC, 2001). . . . . . . . . . . . . . . . . . . . . .
6
2.1
Conceptualization of downscaling and its converse and aggregation, with reference to the resolution of climate model outputs (GCMs and RCMs) and a local
model (Hostetler, 1994). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2
9
Schematic diagram of the resolution of the earth’s surface and the atmosphere
in the Hadley Centre regional climate model Hadley Center (2002). . . . . .
11
2.3
First step of the forecast: selection of a subset of analog dates (Obled et al., 2002). 14
2.4
Second step of the forecast: elaboration of basin-specific conditional distributions (Obled et al., 2002). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
3.1
Principle of the CP definition (Bárdossy and Fulya, 2005). . . . . . . . . . . . .
23
3.2
Effect of a power transformation with λ < 1 (Wilks, 1995). . . . . . . . . . . .
28
3.3
Choosing λ = 1/ βp for correcting the skewness of a precipitation distribution.
28
3.4
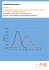
A variety of normal distribution with µ and σ. . . . . . . . . . . . . . . . . . .
29
3.5
A variety of exponential distributions with λe . . . . . . . . . . . . . . . . . . .
30
3.6
A variety of gamma distributions with α and β . . . . . . . . . . . . . . . . . .
31
3.7
Monthly precipitation (mm/day) of 2020’s relative to 1961-1990 generated by
the ECHAM4 A2a scenario (IPCC). . . . . . . . . . . . . . . . . . . . . . . . .
3.8
the ECHAM4 B2a scenario (IPCC). . . . . . . . . . . . . . . . . . . . . . . . .
3.9
38
38
the HadCM3 A2a scenario (IPCC). . . . . . . . . . . . . . . . . . . . . . . . .
39
3.10 Monthly precipitation (mm/day) of 2020’s relative to 1961-1990 generated by
the HadCM3 B2a scenario (IPCC).
. . . . . . . . . . . . . . . . . . . . . . . .
39
3.11 Average bias of MSLP derived from the ECHAM4 and the NCEP in meter from
March to May. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
v
40
List of Figures
June to August. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
September to November. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
December to Febuary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
3.15 Average bias of MF derived from the ECHAM4 and the NCEP in g.m/kg.s from
March to May. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
June to August. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
September to November. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
December to Febuary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
43
4.1
Neckar River Basin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
46
4.2
Annual precipitation amount observed in summer and winter half year in the
Neckar River Basin. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
47
4.3
Distribution of precipitation stations over the Baden-Württemburg.
48
4.4
Wetness index of each CP in summer and winter of the years from 1960 to 1978
. . . . . .
and from 1994 to 1999. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
4.5
Anomaly maps of pressure distribution for CP05 and CP11. . . . . . . . . . . .
49
4.6
Anomaly map of CP12a and CP04b. . . . . . . . . . . . . . . . . . . . . . . . .
53
4.7
Anomaly map of CP01a and CP09b. . . . . . . . . . . . . . . . . . . . . . . . .
53
4.8
Anomaly map of CP12a and CP02c. . . . . . . . . . . . . . . . . . . . . . . . .
53
4.9
Anomaly map of CP03a and CP04c. . . . . . . . . . . . . . . . . . . . . . . . .
54
4.10 Anomaly map of CP09b and CP02c. . . . . . . . . . . . . . . . . . . . . . . . .
54
4.11 Anomaly map of CP04b and CP05c. . . . . . . . . . . . . . . . . . . . . . . . .
54
4.12 Anomaly map of CP12a and CP04d. . . . . . . . . . . . . . . . . . . . . . . . .
54
4.13 Distribution of rainfall stations within the Neckar River catchment. . . . . . . .
56
4.14 Rainfall probability for the station Sindelfingen conditioned to CPs and MF. .
58
4.15 Rainfall probabilities calculated from the observations and logistic regression
for CP11 (diamonds: modeled rainfall probability; squares: observed rainfall
probability; dashes: confidence level of 95 %). . . . . . . . . . . . . . . . . . . .
60
4.16 Annual cycle of precipitation at stations in the catchment area during validation
[continued]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vi
63
List of Figures
4.17 Annual cycle of precipitation at stations in the catchment area during validation. 64
4.18 Averaged extreme indices over the whole river basin for the spring and the
summer seasons [Validation]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
4.19 Averaged extreme indices over the whole river basin for the autumn and the
winter seasons [Validation]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
4.20 Annual monthly precipitation at Esslingen under the impact of climate change.
69
4.21 River network and gauge stations within the Chirchik River Basin. . . . . . . .
70
4.22 Monthly rainfall amounts observed at the stations of Oygaing, Pskem, Tashkent,
Dukant and Angren, distributed from north to south. . . . . . . . . . . . . . . .
71
4.23 Monthly average temperature observed at the stations of Oygaing, Pskem,
Tashkent, Dukant and Angren, distributed from North to South. . . . . . . . .
72
4.24 Anomaly pressure maps of circulation patterns classified for the Chirchik River
basin: CP01-CP06. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
4.25 Anomaly pressure maps of circulation patterns classified for the Chirchik River
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
4.26 Rainfall probability for the station Tashkent conditioned to CPs and MF. . . .
80
basin: CP07-CP12.
4.27 Rainfall probabilities calculated from the observations and logistic regression
for CP11 (diamonds: modeled rainfall probability; squares: observed rainfall
probability; dashes: confidence level of 95 %). . . . . . . . . . . . . . . . . . . .
80
4.28 Annual cycle of monthly precipitation derived from observation and simulation
out of 2 model settings during calibration [Station: Charvak]. . . . . . . . . . .
81
out of 2 model settings during calibration [Station: Pskem]. . . . . . . . . . . .
82
out of 2 model settings during calibration [Station: Olgaing]. . . . . . . . . . .
82
out of 2 model settings during calibration [Station: Tashkent]. . . . . . . . . . .
83
out of 2 model settings during calibration [Station: Dukant]. . . . . . . . . . . .
83
4.33 Precipitation between observed and simulated of current and future climate
based on ECHAM4 scenarios A2 and B2 [Station: Olygaing]. . . . . . . . . . .
87
based on ECHAM4 scenarios A2 and B2 [Station: Tashkent]. . . . . . . . . . .
88
based on ECHAM4 scenarios A2 and B2 [Station: Dukant]. . . . . . . . . . . .
vii
88
List of Figures
based on ECHAM4 scenarios A2 and B2 [Station: Pskem]. . . . . . . . . . . . .
89
based on ECHAM4 scenarios A2 and B2 [Station: Charvak]. . . . . . . . . . . .
89
5.1
Representative temporal distribution of annual precipitation in the Ouémé basin. 92
5.2
Flowcharts for daily weather generation using the WGEN framework and (a)
Markov chain and (b) spell-length models for the precipitation component (Wilks
and Wilby, 1999). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.3
The ratios between monthly precipitations derived from scenarios and those
from the control run.
5.4
94
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
The ratios between the standard deviation of monthly precipitations derived
from scenarios and those from the control run. . . . . . . . . . . . . . . . . . . 101
5.5
The comparison between monthly precipitation derived from observation, simulation and scenarios at station Kandi. . . . . . . . . . . . . . . . . . . . . . . . 102
5.6
The comparison between monthly precipitation derived from observation, simulation and scenarios at station Natitingou. . . . . . . . . . . . . . . . . . . . . 102
5.7
The comparison between monthly precipitation derived from observation, simulation and scenarios at station Parakou. . . . . . . . . . . . . . . . . . . . . . 103
5.8
The comparison between monthly precipitation derived from observation, simulation and scenarios at station Save. . . . . . . . . . . . . . . . . . . . . . . . . 103
5.9
The comparison between monthly precipitation derived from observation, simulation and scenarios at station Lonkly. . . . . . . . . . . . . . . . . . . . . . . 104
6.1
Relationship between percentile of daily precipitation and the moisture flux . . 109
6.2
Empirical interdependence between the uniformed moisture flux and precipitation [CP01-CP06] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
6.3
Empirical dependence between the uniformed moisture flux and precipitation
[CP07-CP12]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
6.4
Contour maps of Gumbel copula with different values of β (left: β=2; right: β=6)113
6.5
Dependence structure described by the χ2 copula . . . . . . . . . . . . . . . . . 114
6.6
Conditional probability of precipitation with given moisture flux at different
quantiles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
6.7
Dependence derived from the observation (left) and simulation with model A
and B (right) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
6.8
Dependence structure of precipitation and the moisture flux influenced by CP05 119
viii
List of Figures
6.9
Dependence structure of daily precipitation and the moisture flux driven by
CP11
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
6.10 Dependence derived from the observation (left) and simulation with model C
and D(right) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
6.11 Distribution of precipitation based on a variety of m values under the impact of
CP05 at Station FELDBERG/SCHW. (WST)
. . . . . . . . . . . . . . . . . . 122
6.12 Distribution of precipitation based on a variety of value m under impact of CP11
at Station FELDBERG/SCHW. (WST) . . . . . . . . . . . . . . . . . . . . . . 123
6.13 Distribution of rainfall amounts [mm] amongst different models at Station FELDBERG/SCHW. (WST) [Calibration] . . . . . . . . . . . . . . . . . . . . . . . . 123
6.14 Distribution of rainfall amounts [mm] amongst different models at Station FELDBERG/SCHW. (WST) [Validation] . . . . . . . . . . . . . . . . . . . . . . . . . 124
ix
List of Tables
3.1
Diagnostics of classified circulation patterns. . . . . . . . . . . . . . . . . . . . .
43
3.2
Diagnostics of daily precipitation. . . . . . . . . . . . . . . . . . . . . . . . . . .
44
4.1
Statistical analysis of the impact of individual CP on local rainfall events in the
winter [Neckar River basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2
50
Statistical analysis of the impact of individual CP on local rainfall events in
summer [Neckar River basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
4.3
Description of different CP classifications. . . . . . . . . . . . . . . . . . . . . .
51
4.4
Contingency table of classification A and classification B based on observed daily
precipitation from 1960 to 1990.
4.5
. . . . . . . . . . . . . . . . . . . . . . . . . .
52
Contingency table of classification B and classification C based on observed daily
4.7
51
Contingency table of classification A and classification C based on observed daily
4.6
. . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . .
52
Contingency table of classification A and classification D based on observation
from 1960 to 1990. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
4.8
Summary of the most similar CP pairs amongst comparisons of CP classifications. 53
4.9
Comparison of CP classifications A to C.
. . . . . . . . . . . . . . . . . . . . .
55
4.10 Comparison of CP classifications A to C.
. . . . . . . . . . . . . . . . . . . . .
55
4.11 Average correlation coefficients for the net moisture flux and zonal moisture flux
at the different pressure levels. . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
4.12 Correlation coefficients between observed precipitation and simulated precipitation using the CPs classified based on the NCAR and the NCEP data [Calibration]. 57
4.13 Correlation coefficients between observed precipitation and simulated precipitation using the CPs classified based on the NCAR and the NCEP data [Validation]. 58
4.14 Correlation coefficients between monthly precipitations derived from observed
and simulated daily precipitation [Calibration]. . . . . . . . . . . . . . . . . . .
61
4.15 Correlation coefficients between monthly precipitations derived from observed
and simulated daily precipitation [Validation]. . . . . . . . . . . . . . . . . . . .
x
62
List of Tables
4.16 Frequency of critical CPs in winter and summer over a long-term time period [%]. 68
4.17 Frequency of critical CPs in spring and autumn over a long-term time period [%]. 68
4.18 Mean persistence of critical CPs in winter and summer a over long-term time
period [day]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.19 Mean persistence of critical CPs in spring and autumn over a long-term time
period [day]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.20 Maximum persistence of critical CP in winter and summer over a long-term time
period [day]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.21 Maximum persistence of critical CP in spring and autumn over a long-term time
period [day]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
68
4.22 Average precipitation downscaled from A2 and B2 scenarios from 2000 to 2030,
relative to the present climate condition. . . . . . . . . . . . . . . . . . . . . . .
70
4.23 Meteorological data provided by Hydromet in Uzbekistan (1980-2003). . . . . .
72
4.24 Meteorological data obtained from Global Daily Climatology Network (KNMI).
73
4.25 Meteorological data obtained from Russian’s weather server.
73
. . . . . . . . . .
4.26 Statistical analysis of the impact of individual CPs on local rainfall events in
spring [Chirchik River Basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
summer [Chirchik River Basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
77
autumn [Chirchik River Basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
winter [Chirchik River Basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
4.30 Correlation coefficients between moisture flux and rainfall events in winter [Chirchik
River Basin]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
4.31 Precipitation related diagnostic analysis in winter and summer.[1 Skewed normal
distribution with moisture flux;
2
Exponential distribution with moisture flux] .
84
4.32 Precipitation related diagnostic analysis in spring and autumn.[1 Skewed normal
distribution with moisture flux;
2
Exponential distribution with moisture flux] .
85
4.33 Frequency of wet CPs in winter and summer [%]. . . . . . . . . . . . . . . . . .
86
4.34 Frequency of wet CPs in spring and autumn [%]. . . . . . . . . . . . . . . . . .
86
4.35 Mean persistence of wet CPs in winter and summer [day]. . . . . . . . . . . . .
86
4.36 Mean persistence of wet CPs in spring and autumn [day]. . . . . . . . . . . . .
86
4.37 Maximum persistence of wet CP in winter and summer [day]. . . . . . . . . . .
86
4.38 Maximum persistence of wet CP in spring and autumn [day]. . . . . . . . . . .
86
xi
List of Tables
4.39 Average precipitation downscaled from A2 and B2 scenarios from 2000 to 2030
relative to the present climate condition. . . . . . . . . . . . . . . . . . . . . . .
90
5.1
Average and variance of annual precipitation for the years from 1980 to 1995. .
96
5.2
Extreme indices derived from different model’s settings [Wet seasons]. . . . . .
96
5.3
Daily precipitation (mm) for each month derived from the control run (1960-1990). 97
5.4
Daily precipitation (mm) for each month derived from A2 scenarios generated
by ECHAM4 (2000-2030). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.5
Daily precipitation (mm) for each month derived from B2 scenarios generated
by ECHAM4 (2000-2030). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.6
98
Downscaled meteorological variables from A2 and B2 scenarios for 2000 to 2030,
relative to present climate condition. . . . . . . . . . . . . . . . . . . . . . . . .
6.1
98
Standard deviation of daily precipitation for each month derived from B2 scenarios generated by ECHAM4 (2000-2030). . . . . . . . . . . . . . . . . . . . .
5.9
98
Standard deviation of daily precipitation for each month derived from A2 scenarios generated by ECHAM4 (2000-2030). . . . . . . . . . . . . . . . . . . . .
5.8
98
Standard deviation of daily precipitation for each month derived from the control
run generated by ECHAM4 (1960-1990). . . . . . . . . . . . . . . . . . . . . . .
5.7
98
99
Description of the copula-based models. . . . . . . . . . . . . . . . . . . . . . . 117
xii
Description
AC
Annual Cycle
ASCENA
Agence pour la Sécurité de la Navigation Aérienne en
Afrique et á Madagascar
CCA
Canonical Correlation Analysis
CDF
Cumulative Distribution Function
CP
Circulation Pattern
CSIRO
Commonwealth Scientific and Industrial Research Organization (Australia)
CTL
Control Run
DOF
Degree Of Fulfillment
DWD
Deutsche Wetterdienst
ECHAM
European Centre Hamburg Model
EOF
Empirical Orthogonal Function
GCM
Global Circulation Model
GHG
GreenHouse Gases
IPCC
Intergovernmental Panel on Climate Change
KNMI
Koninklijk Nederlands Meteorologisch Instituut
LARs-WG
Long Ashton Research Station Weather Generator
MA
Multivariate Analysis
Met Office
Meteorological Office, UK
MF
Moisture Flux
MLE
Maximum Likelihood Estimator
MSLP
Mean Sea-Level Pressure
NCEP
National Centers for Environmental Prediction
OECD
Organisation for Economic Co-operation and Development
PCA
Principle Components Analysis
xiii
Description
PDF
Probability Distribution Function
PSU/NCAR
the Pennsylvania State University / National Center
for Atmospheric Research numerical model
RCM
Regional Climate Model
REEP
Regression Estimation of Event Probabilities
RIVERTWIN
a Regional Model for Integrated Water Management
in Twinned River Basins
SMHI
Swedish Meteorological and Hydrological Institute
STARDEX
Statistical and Regional dynamical Downscaling of
Extremes for European regions
TWS
Teweles-Wobus Score
UNEP
United Nations Environment Program
UNESCO
United Nations Educational, Scientific and Cultural
Organization
USGS
United States Geological Survey
WMO
World Meteorological Organization
xiv
Abstract
This work was aimed to improve the generation of daily precipitation time series with information from atmosphere. The motivation is to develop a conditional stochastic downscaling model
to well describe temporal and spatial behavior of local precipitation, in particular, the extreme
rainfall events. Thereafter, the generated daily precipitation can be applied to integrate with
other water-related models for climate impact studies.
Global warming has been concerned since the end of last century. The increase of the
temperature may result in various consequences e.g., rises in sea levels, increases in evaporation
and change in intensity and distribution of local climate events, which may further impact the
environment and cause the changes in agricultural production, glacier retreat, water resources
distributions and so on. Therefore, the impact studies must be carried out to understand the
influence of the changing climate and predict its possible consequences in order to mitigate
and adapt to the changing climate.
In the field of hydrology, detailed information is always required to describe the hydrological processes. These detailed information includes the situation of landuse, the condition of
local climate, and the status of soil moisture and others. Precipitation, especially, is of great
concern due to its spatial and temporal variability. Basically, precipitation is a product of
atmospheric motions and physical processes i.e. interactions in the atmosphere on one hand
and an important driving force in the land-atmosphere interactions on the other hand. It is
the result of atmospheric movement. Therefore, it is reasonable to derive information about
precipitation from the atmospheric studies.
The global climate models (GCMs) do produce daily precipitation time series. However,
due to their coarse resolutions and incomplete understanding of climate science, the outputs
of GCMs can not properly describe the processes in detail for the local regions and can not be
directly applied to the hydrological models for studying the hydrological response. A certain
method is required to match the mismatch between two different scales and this method is
“Downscaling”.
In this thesis work, three downscaling methods based on the statistical downscaling were
explored. They are a CP- and Regression-based downscaling approach, a CP- and Copulabased downscaling approach and a multi-site weather generator.
xv
Abstract
The first two methods were both developed based on the circulation patterns. The circulation
patterns can be obtained either from professional knowledge (subjective classification) or from
statistical characteristics derived from the observations (objective classification). The scheme
proposed and investigated here is based on fuzzy-rule logic. It is a method that works on the
concept of fuzzy sets, describing the atmospheric circulations using imprecise statements.
The circulation patterns are useful to capture the information at a large-scale, however, they
are weak in capturing the continuity of the whole natural system. The additional predictors
are therefore required to overcome this drawback. A combined term, moisture flux, is introduced into the pure CP-based downscaling model. The moisture flux is a product of specific
humidity and components of wind speed, describing the convey of the water vapor by the wind
field. It was proved to be highly correlated to the local rainfall events in terms of rainfall
probabilities and rainfall amounts. With the incorporation of continuous moisture flux, a CPand Regression-based downscaling model was developed.
A CP- and Copula-based downscaling model is a further development of the combination of
moisture flux, which was also developed based on the circulation patterns. The relationship
between daily precipitation and moisture flux was described by a joint distribution based on
the concept of copula instead of regression method. By using the concept of copula, the dependence is represented by a copula function, which is a function that couples one-dimensional
uniform distribution functions to a multivariate joint distribution. All the marginal distributions of studied variables are uniformed in the space (0,1). Therefore, any appropriate marginal
distribution is allowed to be selected. Furthermore, the copula function is able to represent
the various dependence structure between the different quantiles of the variables, which makes
it possible to fully reproduce the dependence structure identified from the observations.
The CP-based downscaling model is suitable for the regions located in the higher latitudes,
where the Coriolis force is quite dominant in forming anticyclones and cyclones. For other
regions near to the equator, where the Coriolis force is weaker, the same methodology does
not work properly anymore. To downscale daily precipitation for those lower latitude regions,
a multi-site weather generator was developed. The developed model is a stochastic statistical
downscaling model. It is able to simultaneously generate the reasonable daily rainfall time
series.
The models have been successfully applied to the different river basins located in the contrasting climate zones. The models delivered promising results. The critical CPs for specific
river basins were identified and they could be used to explain the large rainfall events. The
generated daily precipitation are comparable to historical observations and can be used as
input to other water-related model for the river basin management studies under the impact
of climate change.
xvi
Zusammenfassung
0.1 Einleitung
Das Ziel dieser Arbeit ist, die Generierung täglicher Niederschlagszeitreihen durch Informationen aus der Atmosphäre zuverbessern. Das entwickelte Modell soll dabei sowohl das räumliche
und zeitliche Verhalten lokaler Niederschläge beschreiben, als auch extreme klimatische Bedingungen reproduzieren.
Die globale Erwärmung wird seit dem Ende des letzten Jahrhunderts mit Sorge zur Kenntnis
genommen. Der Temperaturanstieg könnte viele Veränderungen zur Folge haben, wie z. B. den
Anstieg des Meeresspiegels, der niedrig liegende Länder wie die Niederlande und Bangladesh
bedroht oder den Anstieg der Evapotranspiration, der den Wasserkreislauf beschleunigt und
die Intensität und Verteilung lokaler klimatischer Ereignisse beeinflusst. Weiterhin pflanzen
sich diese Folgen fort und verursachen Veränderungen der landwirtschaftlichen Produktion,
Gletscherrückgang, Intensitäten der meteorologischen Extreme, im Wasserhaushalt und vielen
mehr. Daher sind Klimafolgenstudien notwendig, um die klimatischen Prozesse zu verstehen, mögliche Konsequenzen vorherzusagen, den Klimawandel abzumildern sowie sich daran
anzupassen.
In der Hydrologie werden Niederschlag-Abfluss-Modelle benutzt, um die Beziehung zwischen
Niederschlag und Abfluss auf verschiedenen räumlichen und zeitlichen Skalen zu beschreiben.
Dafür werden detaillierte Informationen wie die Landnutzung, der meteorologische Antrieb, die
Bodenfeuchte und vieles mehr benötigt, speziell Niederschlag dessen räumliche und zeitliche
Variabilität ihn entscheidend für die hydrologische Modellierung macht. Niederschlag ist im
Grunde einerseits ein Produkt der atmosphärischen Bewegungen und Prozesse, d. h. der Wechselwirkungen, und andererseits ein wichtiger Antrieb des Zusammenspiels von Landoberfläche
und Atmosphäre. Als Produkt der atmosphärischen Strömungen ist es sinnvoll, Informationen
über Niederschlag aus der Atmosphäre abzuleiten.
Auch globale Klimamodelle (GCMs) produzieren tägliche Niederschlagszeitreihen. Aufgrund
ihrer niedrigen Auflösung und Lücken im Verständnis des Klimas können die Ergebnisse solcher
GCMs aber die lokalen Prozesse nicht im Detail beschreiben. Daher können die Rohdaten
nicht direkt in hydrologischen Modellen verwendet werden, um Klimafolgen abzuschätzen. Als
xvii
0.2. METHODIK UND ANWENDUNGEN
Methode um die Differenz zwischen diesen beiden Skalen zu überbrücken dient das sogenannte
”Downscaling”.
0.2 Methodik und Anwendungen
Verschiedene Downscaling Methoden wurden in der Vergangenheit entwickelt. Sie können in
zwei Hauptgruppen eingeteilt werden: statistisches Downscaling und dynamisches Downscaling.
In dieser Arbeit wurden drei Downscaling Methoden untersucht, um die Niederschlagscharakteristik unterschiedlicher Klimazonen zu beschreiben. Dies sind ein Großwetterlagen-RegressionsAnsatz, ein Großwetterlagen-Copula-Ansatz und ein multivariater Wettergenerator.
Die ersten beiden Methoden basieren auf Großwetterlagen (circulation patterns, CPs), die
die großräumigen klimatischen Bedingungen beschreiben. Diese CPs können entweder aus Expertenwissen (subjektive Klassifikation) oder aus den statistischen Eigenschaften der Beobachtungen (objektive Klassifikation) abgeleitet werden. Die objektive Klassifikation kann weiter
in hierarchische und partitionierende Methoden unterschieden werden. Das hier vorgestellte
und untersuchte Schema basiert auf unscharfer Logik (Fuzzy rules) und benutzt das Konzept
der fuzzy sets wobei die atmosphärische Zirkulation mittels unscharfer Aussagen beschrieben
wird. Das Klassifikationsschema besteht aus vier Schritten:
- Transformation der großkaligen Daten;
- Definition der fuzzy rules;
- Optimierung der fuzzy rules und,
- Klassifikation der CPs.
Die atmosphärischen Variablen werden anhand der gesuchten meteorologischen Variablen
ausgewählt, z. B. tägliche Niederschlagszeitreihen für Niederschlags-CPs. Die generierten CPs
sollten die Haupteigenschaften einer bestimmten Großwetterlage bezüglich Niederschlags gut
wiedergeben können.
Die CPs können Informationen auf einer großen Skala gut reproduzieren, ihnen fehlt aber die
Kontinuität des natürlichen Klimasystems. Daher werden zusätzliche Prädiktoren benötigt,
um diesen Nachteil zu korrigieren. In diesem Fall wird ein kombinierter Term, der Feuchtefluss, in die reine CP-Generierung eingeführt. Der Feuchtefluss ist das Produkt der spezifischen
Feuchte und den Komponenten der Windgeschwindigkeit. Er beschreibt den Transport von
xviii
0.2. METHODIK UND ANWENDUNGEN
Wasserdampf mit dem Windfeld. Die Arbeit zeigt, dass der der Feuchtefluss und lokale Niederschlagsereignisse in Bezug auf Wahrscheinlichkeit und Höhe hoch korreliert sind. Im vorgestellten Modell wird daher die Niederschlagshäufigkeit durch die CPs und den täglichen Feuchtefluss
bestimmt und durch eine bedingte logistische Regression beschrieben. Der Einfluss des Feuchteflusses auf die Verteilung der Niederschlagshöhe wird ebenfalls durch ein Regressionskonzept
wiedergegeben. Die diskret-kontinuierlichen Eigenschaften des Niederschlags können durch die
jeweiligen Verteilungen gut erfasst werden. Das resultierende CP-Regressions-basierte Downscaling Modell kann Niederschlagszeitreihen simultan generieren. Die Hauptergebnisse können
folgendermaßen zusammengefasst werden:
- CPs können das repräsentative synoptische Klima erfassen.
- Der Feuchtefluss spielt für lokale Niederschlagsereignisse eine wichtige Rolle, er wird
durch die Beziehung zur lokalen Geographie und Orographie stark beeinflusst.
- In den gemäßigten Breiten der nördlichen Hemisphäre dominiert der westliche Feuchtefluss über andere Einflüss.
- Die Niederschlagshöhe und -wahrscheinlichkeit werden von den klassifizierten CPs und
dem Feuchtefluss beeinflusst.
- Die logistische Regression kann die Niederschlagshäufigkeit durch die Parametri-sierung
nicht-linearer Gleichungen mit dem Feuchtefluss als Prädiktor für die Niederschlagswahrscheinlichkeit sinnvoll beschreiben.
Das Modell konnte erfolgreich im Neckareinzugsgebiet in Deutschland (Mitteleuropa) und
im Chirchikeinzugsgebiet in Usbekistan (Zentralasien) angewendet werden. Die jeweiligen CP
Zeitreihen für beide Gebiete wurden erzeugt und konnten die Haupteigenschaften der lokalen
atmosphärischen Zirkulation beschreiben. Die Modelleffizienz wurde anhand des Niederschlagsjahresgangs und verschiedener Extremindizes gemessen und verbesserte sich gegenüber dem
reinen CP-basierten Downscaling Modell.
Zusätzlich wurde ausgehend von den CPs ein komplett neues CP-Copula-Down-scaling Modell entwickelt. Die Beziehung zwischen täglichem Niederschlag und Feuchte-fluss wird durch
eine gemeinsame Verteilung beschrieben, basierend auf dem Konzept der Copulas, die neuerdings in der Hydrologie für multivariate Statistik eingesetzt werden.
Aus statistischer Sicht sind Copulas Funktionen, die eindimensionale Gleichverteilungen
mit einer multivariaten gemeinsamen Wahrscheinlichkeitsverteilung verknüpfen. Kurz gesagt,
sind es Sammlungen multivariater Verteilungen, deren Randverteilungen im Raum (0,1) gleichverteilt sind. Daher gibt es keine Beschränkungen bezüglich der Auswahl der Randverteilun-
xix
0.3. DISKUSSION UND SCHLUSSFOLGERUNGEN
gen, was der Analyse der Zusammenhänge zwischen den univariaten Verteilungen mehr Flexibilität gibt.
Im Unterschied zum Regressionsmodell kann das Copula Modell die unter-
schiedlichen Abhängigkeitsstrukturen verschiedener Quantile der Variablen wiedergeben, wodurch
die Zusammenhänge der Beobachtungen besser erfasst werden.
In dieser Arbeit wurden der Gumbel Copula und der χ2 Copula als gemeinsame Verteilung
angewandt. Eine transformierte schiefe Normalverteilung und die Exponentialverteilung dienen als Randverteilungen, um tägliche Niederschlagszeitreihen zu reproduzieren. Dieses neue
Modell wurde im Neckareinzugsgebiet angewandt und die folgenden Schlussfolge gezogen:
- Zusammenhänge zwischen Niederschlag und Feuchtefluss sind abhängig vom jeweiligen
Quantil.
- Bei höheren Quantilen des Feuchteflusses ist ein höheres Quantil des Niederschlags am
selben Tag wahrscheinlich.
- Der χ2 Copula repräsentiert die gemeinsame Verteilung von täglichem Niederschlag und
Fechtefluss besser als der Gumbel Copula.
- Die Exponentialverteilung reproduziert große Niederschlagsereignisse am besten.
Das CP-basierte Downscaling Modell ist in mittleren bis höheren Breitengraden, in denen Hoch- und Tiefdruckgebiete durch die Corioliskraft rotieren, gut geeignet. Nahe des
Äquators, wo die Corioliskraft schwächer ist, funktioniert die Methode schlechter. Um täglichen
Niederschlag in diesen Breiten herunterzuskalieren, wurde ein multivariater Wettergenerator
entwickelt. Dieser ist ein stochastisches Downscaling Modell für tägliche Niederschlagszeitreihen basierend auf der transformierten schiefen Normalverteilung. Auch dieses Modell konnte
erfolgreich simultane tägliche Niederschlagszeitreihen generieren.
0.3 Diskussion und Schlussfolgerungen
Der Einfluss des zusätzlichen Prädiktors Feuchtefluss zur Verbesserung des reinen CP-basierten
Downscaling Modells wurde untersucht. Es wurde gezeigt, dass das Modell durch die Einbeziehung des Feuchteflusses das räumliche und zeitliche Verhalten lokaler Niederschlagsereignisse
besonders im Falle von Extremereignissen besser beschreiben kann.
Die vorgestellten Modelle wurden zuerst im Neckareinzugsgebiet in Deutschland entwickelt
und anschließend in zwei Einzugsgebiete in gegensätzlichen Klimazonen in Westafrika und Zentralasien transferiert und angewandt. Die Modelle wurden an das synoptische Klimageschehen
in diesen Regionen angepasst, um sinnvolle tägliche Niederschlagszeitreihen zu generieren.
xx
0.3. DISKUSSION UND SCHLUSSFOLGERUNGEN
Das CP- und regressionsbasierte Modell konnte erfolgreich im Neckar- und Chirchik-einzugsgebiet
angewendet werden, obwohl die klimatischen Bedingungen und die Datenverfügbarkeit in beiden Regionen sehr unterschiedlich sind. Die Modelleffizienz wurde durch eine diagnostische
Analyse bestimmt, die zeigte, dass Extremindizes zur Evaluierung der interannuellen Variabilität verbessert werden konnten. Unter den verschiedenen Modellsetups konnten die Generatoren mit transformierter Normalverteilung und Exponentialverteilung am zuverlässigsten
sinnvolle Niederschlagszeitreihen generieren. Die Modelle können im allgemeinen den Winterniederschlag sehr gut reproduzieren, sind etwas schwächer in den Übergangszeiten und am
schwächsten im Sommer. Dies wird durch die unterschiedlichen Niederschlagsmechanismen in
Winter und Sommer hervorgerufen. Die vertikale Verteilung des Feuchteflusses könnte genauer
bezüglich ihres Einflusses auf die sommerlichen Konvektiver-eignisse untersucht werden.
Die Fähigkeit des Modells Extremereignisse wiederzugeben wurde zwar verbessert, dennoch
bleiben Unterschiede zwischen Beobachtung und Simulation bestehen. Das Auftreten großer
Niederschlagsereignisse wird beispielsweise unterschützt. Deshalb wurden Copulas als Alternative zum CP-Regressions-Modell untersucht.
Dieses neue Modell hat im Neckareinzugsgebiet gezeigt, dass die Zusammenhänge zwischen
verschiedenen Quantilen der Randverteilungen besser erfasst werden kann. Auch die Reproduktion der Extrema wurde verbessert. Nicht zuletzt haben Copulas den Vorteil, dass die
Randverteilungen unabhängig von der gemeinsamen Verteilung sind. Dies bietet die Flexibilität, die passende Randverteilung zu wählen um die untersuchte Variable zu beschreiben.
Die gefundenen Zusammenhänge können durch existierende oder neu konstruierte Copulafamilien wiedergegeben werden. Die Konstruktion neuer Copulas anhand der vorgegebenen Eigenschaften ist einfach. Daher bietet diese Methode vielversprechende Möglichkeiten der Anwendung in der Klimaforschung.
xxi
1 Introduction
Water is an essential universal element that no creature is able to live without. It covers 70%
of the earth’s surface, however, the available amount of fresh water is quite limited (Peixoto
and Kettani, 1973): only 2.5% of the total water can be used as fresh water; nearly 70% of
that amount is frozen in the icecaps of Antarctica and Greenland, and most of the remainder
is stored as soil moisture or contributes to be the groundwater. In reality, less than 1% of the
world’s fresh water (about 0.007% of all water on the earth) is accessible for direct human uses.
Furthermore, this amount of available water may become less and less, for instance, UNESCO
predicted 30% reduction in fresh water quantity in the next twenty years (UNESCO, 2003).
Due to an unbalanced distribution of water resources, the real situation in different regions
around the world can be even worse.
1.1 Problem and motivation
1.1.1 Hydro-meteorology
Precipitation is a major water resource for local regions and also an important component
in the hydrological system. Basically, it is a product of atmospheric motions and physical
processes i.e. interactions in the atmosphere on one hand and an important driving force in
the land-atmosphere interactions on the other hand. The interactions amongst the different
components can be visualized in Figure 1.1: water evaporates from the surface of the ocean
and the ground; the moist air arises and is transported; finally, the condensed water falls down
to the surface as precipitation.
In conventional hydrology, precipitation is always considered as a main triggering force. With
the aid of derived area characteristics for the catchment, the temporal and spatial behavior of
hydrological variables such as stream flow can be modeled using an appropriate hydrological
model. Unlike temperature, precipitation contains its unique property of being regionally
and temporally unevenly distributed. Such property intensifies water-related events such as
floodings and droughts, which subsequently negatively impact agriculture, hydraulic structures,
forestry and human health. Precipitation is therefore a crucial variable in a wide range of
disciplines related to natural, socio-engineering and economic systems.
1
1 Introduction
Meteorology is one of the natural science disciplines. It is the study of the formation and
evolution of the weather processes and further forecasting. It comprises an interdisciplinary
field with hydrology. With the help of information observed in the earth’s atmosphere and
surface such as pressure, water vapor in the atmosphere and precipitation, temperature, wind
movement on the earth’s surface, numerous atmospheric variables and their interactions are
described by fluid mechanisms and numerical expressions.
Figure 1.1: Circulation of water around, over and through the Earth (USGS 1973).
Meteorology attempts to study all the weather states. One of the important weather states is
precipitation. It is the product of the condensation of atmospheric water vapor that is less than
0.001% of the total water amount. Compared with 97.5% in the oceans and 2.4% on land, the
amount contained by the atmosphere is really a tiny portion, it however impacts the available
freshwater on the earth significantly. In Figure 1.2, three main reservoirs of the water cycle are
presented. They are atmosphere, oceans and land. Based on the volume and transportation
rate of the individual reservoir, it can be calculated that water remains in the atmosphere for
about eight days before condensing and falling to the ground as precipitation, which is a much
shorter residence time than that required for the groundwater recharge. Hence, the amount
of water vapor contained in the atmosphere and how long it remains there are quite sensitive
when monitoring the intensity of the water cycle, which most probably affects synoptic weather
state in the local regions.
Obviously, precipitation can not be considered as a single element. Instead, it is an element
of environmental cycle. Knowledge of both hydrology and meteorology are required to get a
2
1 Introduction
ATMOSPHERE
324 x 1012m3 /year
PRECIPITATION
361 x 1012m3 /year
EVAPORATION
0.013 x
1015
m
PRECIPITATION
99 x 1012m3 /year
3
62 x 1012m3 /year
EVAPORATION/
TRANSPIRATION
LAND
33.6 X 1015 m3
OCEANS
RUNOFF/
GROUNDWATER
37 x 1012m3 /year
1,350 x 1015 m3
Figure 1.2: Water budget amongst atmosphere, land and ocean (Peixoto and Kettani, 1973).
complete overview of a precipitation event and to assess its impact on other hydro-phenomenon
such as water quality, water distribution, agricultural productivity and other natural processes.
1.1.2 Global warming
Since the end of the past century, the global climate has shown the noticeable changing rate
in terms of change in temperature, which may in turn cause the changes in the amount and
patterns of precipitation in some regions too. For instance, weather tends to be drier in the
subtropical regions like the Mediterranean basin, South Africa, Southern Australia, while more
precipitation is projected in near-equatorial regions (IPCC, 2007). Global warming is supposed
to explain those phenomena. Numerous studies have been carried out and are being carried
out to understand the climate process and further predict its possible consequences.
The concept of global warming was first studied by a Swedish chemist Svante Arrhenius one
hundred years ago. He was the first to formulate the concept that a doubling CO2 concentration
in the atmosphere could cause the increase of the surface temperature up to 5 ◦ C through the
greenhouse effect.
From that time on, more and more efforts have been put into the study area of climate
system; several subsystems are incorporated into the whole climate regime one after the other,
particularly, with the development of computer science. Several grand milestones have emerged
since the last century:
3
1 Introduction
- In the 1900’s, the Norwegian scientist Vilhelm Bjerknes founded the modern science of
weather forecasting with his studies of fundamental interaction between fluid dynamics
and thermodynamics.
- In 1922, Lewis Fry Richardson proposed a scheme for weather forecasting using differential equations.
- In the 1940’s, Smagorinski, Charney, von Neumann developed a numerical weather predictor, the oceans were considered as a dynamical component of the whole integral system.
- In the 1950’s, Manabe developed the first climate model.
- In the 1960’s, the chaotic theory for the atmosphere was first observed and published by
Edward Lorenz, which lead to the current use of the concept of ensembles and uncertainty
analysis.
- Keeling’s and Charney’s work revealed the important role of the biosphere.
In addition, many observation reports were published as well. They reflected the rapid
change of the climate system as a consequence of other components. Temperature was found
to have strong covariance with green house gas for the past 400, 000 years; rapid climate
change was noticed in the past one hundred years. The earth’s average surface temperature
rose 0. 6 ± 0. 2 ◦ C over the past 100 years with two main periods of warming: between 1910
and 1945 and from 1976 onwards. The rate of warming during the latter period has been
approximately double that of the first, and greater than at any other time during the last 1,
000 years (See Figure 1.3).
The increase of surface temperature in turn leads to several consequential effects, for instance:
- Rises in the sea level threaten the low-lying countries such as the Netherlands and
Bangladesh.
- Increased evaporation results in the acceleration of the hydrological cycle and impacts
the intensity and distribution of local climate events such as precipitation.
Concerning climate change, one important scholar has to be mentioned: Vladmir I. Vernadsky. This Russian-Ukrainian mineralogist and geochemist pointed out the importance of
living organisms to the whole biosphere. He considered the biosphere as a unique region of the
earth’s crust occupied by life and pointed out that no chemical forces at the earth’s surface
are stronger than living organisms. His idea can be somehow constructed as Figure 1.4, that
4
1 Introduction
the climate system is an interdisciplinary field: on one hand, human activities impact their
socio-economic development, which change the other components in the natural world and
finally indirectly affect the climate conditions; on the other hand, the changed climate affects
human behaviors as well.
Figure 1.3: Variation of the Earth’s surface temperature (IPCC Working Group I).
“To understand the scientific basis of the risk of human-induced climate change and to assess its potential impacts and options for adaption and mitigation amongst climate change,
emissions and concentrations, socio-economic development and impact on human and natural systems”, the International Panel on Climate Change (IPCC) was founded by the World
Meteorological Organization (WMO) and the United Nations Environment Program (UNEP)
in 1988. IPCC defined various scenarios with specific emphasis on population, fuel energy,
5
1 Introduction
economic developing level and so on up to the year 2100. Today, their outcomes are widely
used as guidelines for climate impact studies and policies making.
Figure 1.4: Impact of Climate Change (IPCC, 2001).
1.2 Need for downscaling
Downscaling is a mathematical process. It has been developed based on the understanding of
the interconnection between different working scales, in this case, hydrology and meteorology
and is conducted with the help of information provided by global circulation models (GCMs).
GCMs are one of the most useful products of climate-related studies. Based on the physical
laws for atmospheric motions, the knowledge of atmospheric compositions and behavior has
been studied in the scientific society. It is a kind of physically-based atmospheric model
describing the known processes in the earth’s climate system and their possible interactions
and feedback processes; it is done by integrating the acknowledgement of ocean, atmosphere,
land and sea ice.
Their aims are to reproduce the large-scale changes in the present and past climate situations
considering the internal and external driving forces and feedbacks in the climate system. They
are expected to predict the possible climate conditions in the future. Initially, the ocean model
and the atmosphere model were developed separately. Recently, they have been combined and
considered as a unit to provide the projection of present and future climate conditions. The
horizontal resolutions of those models are generally at hundreds of kilometers. The models show
6
1 Introduction
a significant ability to incorporate complex processes of the global system, and represent their
outcomes at continental and/or hemispheric spatial scales and monthly temporal scales. They
are, however, still weaker in representing the local subgrid-scale features and dynamics (Wigley
et al., 1990; Carter et al., 1994). This weakness is mainly due to an incomplete understanding
of the complexity of mesoscale atmospheric processes occurring at relatively small scales such
as cloud formation, moist convection and so on (Risbey and Stone, 1996). Apart from that, due
to high computational cost, global numerical models only solve the primary energetic motions,
which are not enough for those motions occurring at the order of several kilometers in scale
(Hack, 1994). Currently, what those parameterized variables present is only the large-scale
averages, but not the real local features.
Hydrological models describe the relationship between rainfall and runoff on different spatial
and temporal scale. They require detailed information with respect to landuse, meteorological
input and soil moisture, etc, especially precipitation whose spatial and temporal variability
makes it very crucial in hydrological modeling. Running a hydrological model with outputs
derived directly from GCMs can definitely not capture the local variabilities. Downscaling is
therefore necessary for bridging the mismatch between the two different scales and to derive
information for a region at a finer resolution from that provided by coarse-resolution GCMs.
1.3 Objectives
It is widely acknowledged that climate change is induced by anthropological impacts and in
return it impacts human and natural system as well (IPCC, 2001). In order to estimate the extent of human activity on the climate change and its consequential changes, the understanding
of atmospheric motions must be improved. In the field of impact study, the needs to understand
the regional processes and to evaluate their consequences of large-scale changes are increasing.
Knowledge of local variability is of great importance. Compared with global processes, the
processes occurring at a regional scale are often quite complicated due to the impact of global
forcing and circulations, together with local characteristics such as topography.
The main goal of this study is to develop a more robust downscaling approach using a
statistical method. The method is supposed to reflect the discrete-continuous property of
daily precipitation and its spatial variability. The model is developed for reproducing average
rainfall time series, with emphasis on the extreme events. Finally, the developed model can be
further applied to:
- Climate impact studies.
- Coupling with rainfall-runoff model.
7
1 Introduction
- Coupling with other hydro-modeling such as water quality, ecological models, etc.
8
The term “Downscaling”may be new to those who have not had experience in the interdisciplinary field studies. Downscaling is a procedure that aims to obtain the finer-resolution
atmospheric knowledge from information generated by relatively coarse-resolution global climate models (GCMs) in the context of hydro-meteorology. The significant differences amongst
spatial resolutions adopted by individual climate-related models can be seen in Figure 2.1.
Figure 2.1: Conceptualization of downscaling and its converse and aggregation, with reference to the
resolution of climate model outputs (GCMs and RCMs) and a local model (Hostetler,
1994).
A variety of downscaling techniques have been developed in the past years. They can be
categorized into two major groups: dynamical downscaling and statistical downscaling (Giorgi
and Mearns, 1991).
Dynamical downscaling uses a limited-area, high-resolution model (a regional climate model,
9
or RCM) driven by boundary conditions from a GCM to derive smaller-scale information.
It aims to study the complex procedures using physical explanations that are normally too
sophisticated to be solved and a large amount of available observations are always required.
Nevertheless, it provides the possibility to better understand internal responses amongst subprocesses. Statistical downscaling focuses on studying the dependencies amongst physicalbased procedures and local climate variables using statistical tools and methodologies.
Dynamical-statistical downscaling is a hybrid approach, the combination of the two aforementioned approaches.
2.1 Dynamical downscaling
Dynamical downscaling is a process-based method that extracts high-resolution information
about climate or climate change from the coarse-resolution GCMs. There are three commonly
used dynamical downscaling approaches (Rummukainen, 1997):
- Running a regional scale limited area model (LAM) with the coarse GCMs output as
geographical or spectral boundary conditions
- Performing global-scale experiments with high-resolution AGCMs using the coarse GCMs
as initial and partial boundary conditions
- Using variable-resolution global models that enable to run at the high-resolution over the
area of interests
All of these approaches aim to give a physical representation of the climate system, which is
distinguished from statistical downscaling to be introduced.
Presently, a commonly used dynamical downscaling tool is a regional climate model (RCM),
which is run on a regional scale with a nested limited area of finer resolution within a global
circulation model. There are several RCMs that have been developed and are being developed
worldwide such as RCM by Hadley Center, UK and by SMHI, Sweden.
The horizontal resolution of those RCMs (typically 50 km) is much finer than the GCMs.
The outputs of dynamical downscaling are generally much better in representing the local
phenomena induced by the main local control factors such as topography; however, it shares
the same drawbacks as the other downscaling methods due to their intimate relationship with
the performance of GCMs. The uncertainties generated by GCMs are likely to be propagated
through the pure dynamical downscaling procedure. Additionally, the high computational
demanding is also always required.
To run a regional model, the lateral boundary condition and initial condition are always
required. Those running conditions include:
10
Figure 2.2: Schematic diagram of the resolution of the earth’s surface and the atmosphere in the
Hadley Centre regional climate model Hadley Center (2002).
11
- Topography and landuse information
- Observation data
- Gridded atmospheric data such as horizontal winds, temperature, pressure and moisture
field at all different pressure levels
These boundary information can come from future analysis (scenarios), or from real time
analysis (global circulation model), or from the uplevel coarser simulation (one-way nesting).
RCMs have evolved with the development of GCMs. They have been modified from hydrostatic dynamic to non-hydrostatic dynamic, from one-way nesting to multiple-way nesting,
additionally, more physical options have been developed and coupled with the whole system.
To date, the current version of RCMs such as MM5 has been developed as a limited-area nonhydrostatic, terrain-following sigma-coordinate model. Its working domain is generally about
100 km2 with a resolution of 20 to 60 km, or even as fine as 4 km.
Compared with GCMs, RCMs have been proved to provide a better description and representation of a local processes. However, they still contain the following shortcomings:
- RCMs use the output of a GCM as their initial and boundary conditions. Therefore, any
bias underlying the GCM is subject to be automatically transferred to the RCM .
- Both GCMs and RCMs are affected by physically-based model disadvantages. In fact,
the weaknesses caused by an incomplete understanding of the physics governing the
atmospheric systems are more significant than those caused by using a coarse resolution.
The performances of both GCMs and RCMs can not be enhanced unless the sub-grid
physical processes are better understood. (Risbey and Stone, 1996).
- High requirement of data. For instance, HadRM3, developed by the Hadley Center in
England. The HadRM3 needs data at 19 levels in the atmosphere (from the surface to
30 km in the stratosphere) and 4 levels in the subsurface.
- Finer spatial resolution requires finer time resolution to secure numerical stability. Consequently, RCMs consume expensive computer resources due to the large data set and
complexity of the models.
RCMs are able to achieve better results on a regional scale in comparison with GCMs.
On the other hand, they are quite computer-intensive and have problems related to sub-grid
parameterizations within models that might not be able to be improved at the current scientific
level.
12
2.2 Statistical downscaling
The atmospheric processes are always complex and uncertain. The involved uncertainties
mainly stem from two sources. One is caused by the incomplete observations. Lorenz (Lorenz,
1969) pointed out that the time evolution of non-linear, deterministic dynamical systems like
the atmosphere is very sensitive to the initial condition. A slight difference in the initial condition will lead to a quite large divergence. With a lack of complete and accurate observations,
it will never be possible to represent the climate condition as it really should be. The other is
caused by incomplete understanding of the physics of atmospheric motions, for instance, many
physical processes such as the formation of clouds occur on too small of a scale to be represented by a coarse-resolution model. These two weaknesses created the obstacles that hinders
the development of the deterministic model system. The deterministic forecast of atmospheric
behavior done by a dynamical model will thus always contain uncertainties and statistical
methods will always be needed to evaluate and quantify the corresponding uncertainties.
Statistical downscaling is another important downscaling approach. It can be generally
formulated below (Zorita and von Storch, 1999):
1. Identify the regional climate parameter of interest, R, for instance, precipitation or temperature.
2. Find climate parameter L at large scale which,
- Controls R by R = F(L, α) + with a vector of unknown stochastic parameters
(α1 , . . . , αm ). The represents the part of R not described by F.
- L is reliably simulated in a climate model.
3. Use paired samples (R, L) from historical records to fit α such that k k = k R - F(L,
α) k = min
4. Verify the fitted model R = F(L, α) by means of independent historical data
Statistical downscaling has been developed based on two basic assumptions:
- Dependence between the large-scale and local variables can be described using a statistical
relationship.
- These relationships remain unchanged under the future climate conditions.
Based on these two assumptions, a variety of statistical downscaling methods have emerged.
They are multi-regression methods (Kim et al., 1984; Wigley et al., 1990); neural networks, similar to non-linear multiple regressions (Weichert and Büger, 1998; Trigo and Palutikof, 1999);
13
canonical correlation methods (von Storch et al., 1993; Heyen et al., 1996) and circulation-based
methods by which the specific patterns are used to classify and describe the large-scale climate
conditions (Cubasch et al., 1996; Hewitson and Crane, 1996; Schubert and Henderson-Sellers,
1997).
2.2.1 Analog approaches
The analog method is probably the simplest technique to conduct statistical downscaling. It
was initiated by Duband in the 1970’s (Duband, 1980) and was generally used as a benchmark
for other models. The model’s principle implies that the “similar”large scale circulations
should result in the “similar ”local effects. Past synoptic conditions found in historical archives
similar to the target day should provide information on local conditions, such as the amount
of precipitation under similar conditions. The analog method can be considered as a special
case of the weather pattern based method.
To apply this approach, it is required that (i) the synoptic patterns should be quasi stable for
the study area; (ii) the local variable of interest should be partly related to the synoptic patterns
and to the local features; (iii) for a given day, the part explained by the synoptic pattern should
be similar to the observation attained in the analogous situations (Lorenz, 1969). To fulfill
these requirements, the sufficiently-long observation records are always required to ensure the
analog of the synoptic patterns can be found and corresponding local variables are available.
Figure 2.3: First step of the forecast: selection of a subset of analog dates (Obled et al., 2002).
Generally, the analog is identified from a subset of synoptic variables such as geopotential
height, sea level pressure, etc. The proper quantitative criterions are needed to evaluate the
14
Figure 2.4: Second step of the forecast: elaboration of basin-specific conditional distributions (Obled
et al., 2002).
15
similarity between the daily patterns. These criterions can be Euclidian distance, correlation,
or score index like Teweles-Wobus Score (TWS) (Tweles and Wobus, 1954; Obled et al., 2002).
The analog can be presented using EOF patterns or circulation patterns. The EOF patterns
are identified using Empirical Orthogonal Function analysis. With EOF analysis, the representative synoptic patterns are filtered out and the similarity is presented by the distance between
coordinates between the EOF space and projection of synoptic variables onto the EOF patterns
(Trigo and Palutikof, 2001). The circulation patterns are the patterns representing the atmospheric circulations. They can be classified by different techniques, for example, fuzzy-rule
based classification and k-mean clusters.
Given the synoptic patterns of the simulated day, the most similar situations in a longperiod meteorological archive is selected as the first step to compose a subset of analogs of
local variables of interest, for example, daily rainfall amount. Secondly, a proper distribution
such as a gamma distribution can be fitted to the selected subset, considering the frequency
of non-precipitation days. Such conditional distribution is to be utilized for precipitation
generation. The precipitation generation under the climate change scenarios derived from
GCM follow the same procedure as the aforementioned description. The schematic process is
presented in Figure 2.3 and 2.4.
The analog method is simpler and easier to conduct, however, the limitations are still there.
First, long homogenous observations are always required, especially, for extreme events; secondly, the maximum or minimum amount of modeled variables can never exceed that in the
observed archives.
2.2.2 Circulation pattern (CP) based approaches
The circulation based method is one of the most important alternatives in the climate research
area (Hay et al., 1991; Wilby and Wigley, 1994). It differentiates the long-term historical
observations into several representative patterns, and each pattern is supposed to describe
certain climate condition in the study area. In contrast to the other approaches, multi-grid
points rather than a single grid point are used to capture the local climate circulations over a
large area.
In general, classification procedures are based on either professional knowledge (subjective
classification) or statistical characteristics derived from the observations (objective classification).
The subjective classifications are conducted with long-term collecting data and experts’
knowledge of the local study area. They are normally classified based on air pressure distribution over a certain window. One well-known subjective classification is the Hess and
Brezowsky CPs, used by the German Weather Service. The CPs are classified using air pres-
16
sure distribution in Western Europe-North Atlantic sector. Hess and Brezowsky differentiated
atmospheric circulations into three main categories: zonal, mixed and meridional types. Each
type is further subdivided according to the movement of frontal zones, the location of high
and low pressure centers, and the cyclonic and the anti-cyclonic rotations. As a result, a total
of 29 CPs and one unclassified CP were generated and are used by DWD (Deutsche Wetterdienst) (Hess and Brezowsky, 1969). The other important subjective CPs include the Schüpp’s
CPs for Switzerland (Schüpp, 1968) and Lamb CPs (Lamb, 1972) for the British Isles. Unfortunately, these methods require long observation series and a good understanding of local
climatic phenomena. Only for a few countries, subjective CPs were developed.
The objective classification is a semi-automated or automated technique that pertains to
mathematical approaches, e.g., hierarchical methods (Johnson, 1967), k-means methods (MacQueen, 1967), cluster analysis (Kysel and Huth, 2003) and correlation methods (Yarnal, 1984).
The objective classification has become more and more important in the field of statistical
downscaling due to its flexible application for individual sites where no subjective classification exists.
The circulation patterns (CPs) are first identified from historical observations using properly defined objective function and a mathematical algorithm. Subsequently, the daily CP
sequence is formulated as a given condition. An appropriate distribution is required to fit the
precipitation in the same group of a circulation pattern. By introducing a random number, the
precipitation time series can be stochastically generated. Climate change scenarios are generated using the revised parameters for the CP definition and the precipitation model using the
large-scale information in the future derived from the runs of GCMs.
The advantage of this method is that the classified circulation patterns can capture the
non-linear property of atmospheric motions and stress the physical relationship between largescale and local-scale. However, it also contains shortcomings. By circulation classification, the
continuities of the nature system are lost.
2.2.3 Regression approaches
The regression method is a commonly-used approach, sometimes referred to as least-squares
regression. Its basic idea is to identify the empirical relationship between local scale predictands
and large scale predictors (Conway et al., 1996). The regression-based downscaling models are
differentiated in the selection of predictors and mathematical transfer functions. To date, the
widely used regression approaches consist of linear and multiple linear regression, principle
components analysis (PCA) and canonical correlation analysis (CCA).
Principle components analysis is the most widely used multivariate statistical technique. It
aims to reduce redundant information containing a large number of variables to a data set
17
with fewer distinguished variables; nevertheless, the major variabilities in the original data set
remains. The advantage of this technique is to exclude correlated variables and retain whose
are mutually uncorrelated.
Canonical correlation analysis can be considered as the further development of PCA: a
“double-barreled PCA”. It individually identifies new variables from both sets of original
variables at a large scale and local scale to maximize the interrelationship between the two
data sets. That is, the information from both the meteorological field and the local hydrological
field can be reduced to be pairs of patterns that exhibit maximum correlation. Additionally,
the identified patterns are independent from each other. The CCA can actually be viewed as a
sort of multiple regression, its objective function is expressed as (Zorita and von Storch, 1999):
X
X
E=
{ft (xi ) −
ak (t) · pk (xi )}2
(2.1)
t,i
R(yi ) =
k
X
ck · ak (t) · qk (yi )
(2.2)
k
Here, pk and qk are the k th pairs of CCA patterns for the large-scale and local variables.
ft (xi ) stands for predictors at atmospheric scale. By minimizing the sum of square root of E
over the whole domain, a linear regression can be solved to get the parameter sets of ak for
precipitation generation and climate change scenarios. Thus, the regional rainfall field, R(yi ),
can be estimated using solved canonical correlations, ck , and amplitude, ak , with information
about local variables.
The regression method is quite simple and analytically tractable. The advantage of this
method is its relatively convenient application and explicit relationship between predictands
and predictors. However, the selected predictands can only represent a fraction of the climate information, when a complete understanding of the whole atmospheric mechanism is not
available.
2.2.4 Weather Generator
Long-term time series of meteorological variables are always demanded for water-related models, however in reality, the observations are generally inadequate in terms of length, completeness and spatial coverage to fulfill the model’s requirement. Additionally, one single realization
is often insufficient to reflect the complex behavior of the climate system when evaluating the
response to climate change. As a solution, weather generators are developed to provide the synthetic time series of weather data that retain the same statistical properties as those identified
from the observation records.
Presently, there are two main types of weather generators: one is named Richardson’s
weather generator; the other is LARs-WG.
18
The concept of Richardson’s weather generator was initially published in 1981 (Richardson,
1981). Four meteorological variables are produced. They are daily precipitation, daily maximum and minimum temperature and daily solar radiation. Precipitation is considered as a
primary variable not only because of its importance for many applications, but also because of
its impact on the other non-precipitation variables. Whether a day is rainy or dry distinctly
differentiates the behavior of temperature and solar radiation, for instance, maximum temperature is likely to be high on a dry day with high solar radiation. Therefore, precipitation is a
pre-condition for generating the rest of the non-precipitation variables.
Accordingly, the weather generator is concerned with two distinct weather states of precipitation probability and precipitation amounts. Almost 150 years ago, researchers started
to explore the persistence of consecutive dry and wet days (Newnham, 1916) and to demonstrate it using mathematical representations (Williams, 1952; Longley, 1953). In 1962, Gabriel
and Neumann proposed to use a simple, first-order Markov chain for precipitation occurrence,
which is generally adopted by most of the current weather generators.
It is stated that the probabilities of future states depend on the current state. Theoretically,
the influence can even be traced back to infinite days before, it can be expressed as below:
P r{Xt+1 |Xt , Xt−1 , Xt−2 , ..., X1 } = P r{Xt+1 |Xt }
(2.3)
The whole model is defined by the following conditional probabilities:
P00 = P r{no precipitation on day t|no precipitation on day t-1}
(2.4a)
P01 = P r{precipitation on day t|no precipitation on day t-1}
(2.4b)
P10 = P r{no precipitation on day t|precipitation on day t-1}
(2.4c)
P11 = P r{precipitation on day t|precipitation on day t-1}
(2.4d)
Additionally, the other two important properties of precipitation occurrence can be derived
from the above conditional probabilities. They are average relative frequency of precipitation
days π and 1-lag autocorrelation r1 .
π=
P01
1 + P01 − P11
(2.5)
r1 = P11 − P01
(2.6)
The length of wet and dry spells generated by the Markov Chain model is assumed to be
independent, it can be presented using geometric distribution where p stands for dry spells
and 1-p for wet spells:
P r{X = x} = p · (1 − p)x−1 , x = 1, 2, 3 ...
19
(2.7)
With the aid of these parameters, the daily precipitation occurrence can be defined through
the random process. A random number is first drawn from the interval between 0 and 1;
whether the simulated day is dry or wet is then determined depending on the condition of
the previous day. If the previous day is wet, then the simulated day is wet if the random
number ≤ P11 , otherwise, it is dry. If the previous day is dry, then the simulated day is wet
if the random number ≤ P01 , otherwise, it is dry. The above parameters are normally defined
separately for each month to contain annual cycle of precipitation occurrences.
Another important weather generator, LARs-WG, is developed based on the concept of
Racsko (Racsko et al., 1991) and Semenov and Barrow (Semenov, 1997). It chooses a semiempirical distribution to present wet and dry spells instead of the Markov chain model. The
random number is generated alternatively from the distributions for wet and dry spells. In
comparison with Richard’s, this distribution is flexible and can approximate a wide variety of
shapes by adjusting the intervals of the distribution, however, it is more complicated.
After determining the precipitation occurrence of the simulated day, a suitable distribution
is required to be selected for rainfall generation. Todorovis and Woolhiser (1975) were the
first to generate precipitation using the Markov chain model with a statistical model. Later
on, an exponential distribution that was chosen by them was adopted by Richardson as well.
The other researchers proposed other distributions such as the gamma distribution (Katz,
1977; Wilks, 1992) and the mixed exponential distribution, which was a combination of two
exponential distributions (Woolhiser and Pegram, 1979).
Unlike precipitation, other meteorological variables are relatively easier to be modeled. They
are evaluated with the Auto Regressive Moving Average (ARMA) method. The governing
equation was suggested by Matalas in 1967 (Matalas, 1967) as shown below:
Z(t) = [A] · Z (t − 1) + [B] · ε (t)
(2.8)
where Z(t) and Z(t-1) are K-dimensional vectors for current day’s and previous day’s nonprecipitation variables respectively. ε(t) is a matrix, depicting errors that are generated by
the standard normal distribution. [A] and [B] are K by K matrices of parameters reflecting
autocorrelation and covariance amongst meteorological variables on the same day.
Different from previous statistical downscaling approaches, weather generators investigate
the climate change impacts based on the monthly statistics of local variables derived from
GCMs, i.e., monthly mean and the variance of precipitation. Impact of the climate change are
reflected by the changes in the statistical properties between control runs and scenario runs.
20
3 Development of a new
circulation-pattern-based downscaling
scheme
The model to be described is a new conditional statistical downscaling model for generating
precipitation time series at a daily scale.
It links local rainfall events with classified circulation patterns (CP) using conditional distributions. Different from pure CP-based downscaling models, it couples potential atmospheric
predictor that provides extra information in addition to CPs. With consideration of spatial
covariance in the study area, the model is able to simultaneously downscale daily precipitation
at multiple sites.
3.1 Fuzzy-rule based classification scheme
3.1.1 Methodology
To implement the circulation pattern based approach, the first step is to classify the circulation
patterns that describe the synoptic climatic phenomena.
As mentioned in Chapter 2.2.2, the classification procedures are conducted based on either
professional knowledge of atmospheric motions (subjective classification) or statistical characteristics derived from observations (objective classification). In the category of objective
classification, there are also many approaches to generate circulation patterns, e.g, hierarchical
methods, k-mean methods. The scheme that is proposed and investigated here is based on
fuzzy-rule logic.
Fuzzy-rule-based classification is one of the objective classifications. It works on the concept
of fuzzy sets (Zadeh, 1965), using imprecise statements to describe a certain system, in this
case the climate system. The classification scheme for circulation patterns (CPs) follows four
steps: the transformation of large scale data, the definition of the fuzzy rules, the optimization
of the fuzzy rules and the classification of circulation patterns.
According to the meteorological variables to be downscaled, the appropriate atmospheric
21
variables need to be carefully selected. Many atmospheric variables show the dominating
influence of the seasonal cycle, for instance, the daily temperature in the summer is always
higher than that in the winter in the Northern Hemisphere. A certain re-expression method
is required to filter out the noisy information caused by the seasonal impact, this method is
called anomalization.
In the process of producing precipitation circulation patterns, anomalies of normalized mean
sea level pressure (MSLP) serve as a predictor. Each CP is described with a fuzzy rule k
represented by a vector V(k) = (v(1)k , v(2)k , . . . , v(i)k , i=1, n). Here, n is the number of
locations (grid points) and k stands for the CP. v(i)k are the indices of membership functions
corresponding to the selected locations. Based on the membership functions, membership
grades for the anomalies are calculated for a given time t and a given location i. These
membership grades are combined to calculate the degree of fulfillment (DOF) for each fuzzy
rule. As a result, the rule k with the highest DOF is selected as a CP for a specific day. A
detailed description of the methodology can be found in Bárdossy et. al (2002) (Bárdossy
et al., 2002).
To determine the best possible rule sets, each fuzzy rule must be optimized with a local
variable using an appropriate objective function that explains variability in frequency and the
amount of precipitation in a given region. The local variable can be daily or hourly precipitation
or daily discharge. Discharge is a good variable that can be considered as a resultant of areal
precipitation, an integrated response to rainfall events. Especially for extreme cases, the heavy
areal precipitation is a dominant influencing factor for large-scale flooding.
In the work done by Fulya and Bárdossy in 2005 (Bárdossy and Fulya, 2005), several influencing factors were taken into account to link the atmospheric circulation to discharge on a
daily time scale. These factors include the response of catchment runoff to the precipitation
event, the antecedent moisture or vegetation features and high discharge properties, which in
total lead to the delayed reaction to the rainfall events. The delay is determined by the size of
the basin. Hence, the differences in discharge, ∆Q (t), is used instead of the discharge, Q (t),
as shown in Equation 3.1. The discharge increments are supposed to be caused by atmospheric
motions and the reductions are due to the properties of the catchment itself to release water,
this is visualized by Figure 3.1.
∆Q (t) = Q (t) − Q (t − ∆t)
(3.1)
However, there are limitations to applying the discharge-based classification, as described below:
- Discharge time series are not always available.
22
120
Weather
Discharge (m3/s)
80
40
0
Catchment
-40
-80
0
100
200
300
400
Time (days)
Discharge based optimization scheme
Figure 3.1: Principle of the CP definition (Bárdossy and Fulya, 2005).
- Appropriate delay in time needs to be carefully determined.
- There should be no artificial hydraulic structures built in the upstream of river basin,
in other words, the applied discharge time series should present the natural response to
climate conditions and catchment characteristics.
In most cases, daily precipitation is therefore always applied and proved to be an appropriate
local variable to optimize the CP classification.
Depending on different local variables, objective function and random numbers, the defined
fuzzy rules can be different and hence the classified CP sequences can also be different. Two
measures are used to evaluate the performance of the optimization process for explaining the
heavy rainfall events. They are the differences in frequency and magnitude of local variables
between the weather state under specific CP and no specific CP. Here, the local variables can
be daily discharge difference or daily precipitation. See Equation 3.2-3.4.
v
u
T
u1 X
2
O1 (V ) = t
P (CP (t)) − P
T
(3.2)
t=1
1.5
T 1 X Z (CP (t))
O2 (V ) =
−1
T
Z
(3.3)
O (V ) = w1 O1 (V ) + w2 O2 (V )
(3.4)
t=1
23
Where, T is the number of days used for the CP optimization. P (CP (t)) is the probability of
precipitation exceeding the threshold occurring with a given CP. P is the probability of a day
being wet without consideration of CP classification. Z(CP(t)) indicates the mean precipitation
amount or discharge increment with a given CP. Z is the mean of that calculated for all of
the days. The larger the O1 (V ) and O2 (V ) are, the better the optimization is. O(V ) is a
combination of both objectives. By introducing the weighting factor w1 and w2 , the emphasis
of each objective is defined according to the requirement for different CP classifications.
In order to also consider the low flow events, the objective function can be modified. The
impact of CPs on both high and low flow events are considered, the objective function O2 (V )
is reformatted as shown in Equation 3.5, a is a proportional factor.
(
O2 (V ) =
1
T
1
T
(t))
ln( Z(CP
)
Z̄
if
(t))
)
ln( Z(CP
Z̄
· a if
Z(CP (t))
Z̄
Z(CP (t))
Z̄
>1
<1
(3.5)
By using a simulated annealing algorithm, the objective function related to the local variable
is maximized. As a result, generated circulation patterns are optimized to explain both the
frequency and the amount of precipitation.
3.1.2 Consistency analysis
The classification process is a stochastic optimization. As mentioned in the previous section,
using an objective function with different emphasis or using different sets of random numbers
may lead to different resultant circulation time series. The CP time series are therefore nonunique; the consistency analysis is thus necessary to identify the common features shared by
the different classifications and to determine the contained uncertainties.
The dependence between every two CP classifications can be evaluated using a contingency
table and then evaluated with the Pearson’s χ2 test. Pearson’s χ2 test is one of the χ2 tests.
The null hypothesis is that the relative frequencies of the occurrence of observed events follow
a specified frequency distribution. It aims to calculate the difference between the observed and
theoretical frequency for all the possible outcomes. The larger the difference is, the far away
the observations from the assumed distribution is. Its expression is shown with Equation 3.6.
χ2 =
X X (nij − eij )2
r
s
eij
i=1
(3.6)
j=1
Here, i presents a particular CP of one classification, A, and , j, a particular CP of the other
classification B. nij is the number of observed cases where both ith and j th CP occur, and
eij is the number of expected cases where both ith and j th CP occur. If the computed χ2 is
larger than the critical value, then the null hypothesis is rejected and the two classifications are
24
dependent on each other. Once the dependency between every two classifications is defined, the
next step is to estimate the strength of the dependence and prediction ability of a classification
for the other. These can be estimated using the corrected Pearson coefficient and λ statistics.
The calculations are expressed in Equations 3.7 to 3.10:
s
s
min (r, s)
χ2
Ccorr =
2
min (r, s) − 1 χ + n
P
j
λA =
maxi nij − maxi n.i
(3.7)
(3.8)
n − maxi n.i
P
λB =
λsym =
− maxj n.j
n − maxj n.j
P
P
1 j maxi nij − maxi n.i + i maxj nij − maxj n.j
i maxj nij
2
2n − (maxj n.j + maxi ni.)
(3.9)
(3.10)
The higher the corrected Pearson coefficient is, the stronger the dependence is. The larger the
λ values are, the lower the probability of a wrong prediction for another classification, in case
one of classifications is known.
3.2 Coupling atmospheric moisture flux
Based on the conservation law that no element can be created or destroyed, any local changes
of water amount within the whole atmospheric system can only be caused by the interface
changes amongst the three possible states of water. However, over a given study area, the
excesses and deficits of water amounts can still occur due to the atmospheric circulations. In
some regions, there is more evapotranspiration than precipitation, whereas in the other regions
the reverse situation can be observed, which is due to a continuous movement of water cycle
over a global scale, as shown in Figure 1.1.
Wind that is formed due to uneven-heating of the earth plays an important role in conveying
the excesses of water from one region to the other. It is therefore considered as an important
predictor in addition to the sea level pressure. Humidity is another important variable. It
explains the concentration of water vapor in the air. All forms of precipitation including
drizzle, rain, snow, ice crystals, and hail are generated as a result of the condensation of
atmospheric moisture. The higher the humidity, the higher the probability of a rainfall. There
are several variables related to the humidity, e.g., absolute humidity, specific humidity, and
relative humidity. Here, specific humidity (Sh) is adopted. It is a variable describing the
ratio of the mass of the water to the mass of the dry air in a given volume of moist air. The
advantage of using this term is its independence from air temperature.
25
The resultant predictor used in this study is named moisture flux (MF), a combined term
for geotropic wind field and specific humidity. It describes how much water vapor flux is
transported by the wind field into the study area.
M F = Geotrophicwind · Sh
(3.11)
Theoretically, the transport process can be further differentiated into horizontal transport and
vertical transport. The horizontal transport field is expressed by a westerly wind component
u and a southernly component v. The total wind field is described as shown below:
Wind = u + v
(3.12)
The vertical water vapor flux is very important in studying the formation of the convective
events such as summer rainfall.
The relationship between daily moisture flux and local precipitation is proved to be strongly
dependent. Daily moisture flux has significant impact on both rainfall amount and rainfall
probability. The detailed information will be given in the following, Chapter 3.3.
3.3 Conditional multivariate downscaling approach
3.3.1 Precipitation occurrence model
As a key parameter in rainfall occurrence, the determination of the probability of a day being
wet is quite important. In the previous studies, rainfall probability is determined by specific
circulation patterns (Bárdossy and Plate, 1992), the Markov chain model (Richardson, 1981) or
the semi-empirical model (Semenov, 1997). These studies are conducted based on the concept
that the present day’s weather state is dependent on that of the previous day. However, apart
from the weather state, the rainfall probability may depend on continuous meteorological variables as well. To prove this assumption, a particular model for describing rainfall probability
is chosen.
There are two approaches for estimating the required probabilities. One is named regression
estimation of event probabilities (REEP), which is simply a multiple linear regression linking
the rainfall probability to the selected predictands. This approach is quite simple and requires
a lower computational demand, however theoretically, the potential unpleasantness exist. The
resulting probability may be out of the range from between 0 and 1, which is meaningless
for forecast probabilities. Another approach is called logistic regression, a technique dealing
with a binary predictand, e.g., zero or one, true or false. Similar to REEP, it also uses binary
predictands, but fits regression parameters to a non-linear equation.
y=
1
1 + exp(b0 + b1 · x1 + b2 · x2 + ... + bk · xk )
26
(3.13)
In this study, the moisture flux vector is considered as a predictor and rainfall probability
is a predictand, a binary dependent variable. Both the predictor and the predictand are CPdependent parameters. When the precipitation is below the threshold value defined as dry
day, the y value for this day is coded as 0, and otherwise y = 1. The probabilities constrained
by the function of Equation 3.13 lie always between zero and one.
3.3.2 Precipitation amount model
Skewed normal distribution
Normal distribution is theoretically called a Gaussian distribution. Due to its simplicity in
application, it has been widely implemented in various research branches including atmospheric
science. Its probability density function is the famous bell-shaped curve that is expressed as:
f (x) =
1
(x − µ)2
√
· exp[−
]
2 · σ2
σ· 2·π
(3.14)
Precipitation is an example of something that is far away from a symmetrically distributed
variable. In fact, the distribution of daily precipitation is strongly skewed to the right. Most
daily precipitation events are small, but occur frequently, while those with larger amounts are
quite seldom. Therefore, the daily precipitation needs to be reexpressed with a transformation
before it is applied with a normal distribution.
The most commonly used symmetry-producing transformations are the two closely related
functions, expressed as below:

λ

if λ 0

 x
T1 (x) =
(3.15)
ln(x) if λ = 0


 −xλ if λ ≺ 0
and
(
T2 (x) =
xλ −1
λ
if λ 6= 0
(3.16)
ln(x) if λ = 0
The transformations are quite useful when dealing with an unimodal distribution of the
positive data set. Its aim is to change the shape of the distribution using exponentiation. A
particular value of λ exerts the effect on the overall distribution and produces a continuouslychanging set of smoothing data set, however, the degree is different. For λ = 1, the original
data set remains unchanged. For λ > 1, the transformation increases all the values and the
larger values are increased more than the smaller ones. It helps produce symmetry when the
original data set is skewed to the left. The impact of λ on the larger and smaller value is shown
in Figure 3.2. In contrast to λ > 1, the application of λ < 1 treats the data set exactly in the
27
other direction. It reduces all of the data’s value, but affects the larger values more strongly
then the smaller value. Therefore, it is generally applied to data that is originally positively
skewed.
Figure 3.2: Effect of a power transformation with λ < 1 (Wilks, 1995).
To find out an appropriate λ for the distribution of daily precipitation, a set of λ values
has been tested to obtain the optimal λ that corrects skewness. Since precipitation data is
typically skewed to the right, a λ < 1 is chosen. Its effect on the correction of skewness is
shown in Figure 3.3.
βp = 1.67
Probability of precipitation
0.70
βp = 1.5
0.60
0.50
βp = 1.2
0.40
Obs.Prep
βp = 1.1
0.30
0.20
0.10
0.00
0
-0.10
5
10
15
20
25
30
35
40
45
Precipitation [mm]
Figure 3.3: Choosing λ = 1/ βp for correcting the skewness of a precipitation distribution.
The normal distribution is a two-parameter distribution with µ (mean) and σ (standard
deviation). µ is a location parameter that locates the center of the symmetrical distribution,
and σ is a shape parameter that controls the degree of how the distribution spreads out.
28
Figure 3.4: A variety of normal distribution with µ and σ.
The combination of µ and σ ensembles a family of normal distributions as shown in Figure
3.4. The proper normal distribution can be used to represent the data set when these two
parameters are fitted. With a given probability, the corresponding value can be obtained from
the cumulative distribution. Conditioned to precipitation, the negative value is considered as no
precipitation and the non-negative value is recalculated with 1/λ to generate the precipitation
amount.
(
n
Z (t, u) =
0
if P −1 (W n (t, u)) < 0
P −1 (W n (t, u))βp
if P −1 (W n (t, u)) > 0
(3.17)
where Z n (t, u) stands for the daily precipitation amount at time t and location u; W n (t, u)
is a normally distributed random variable for location u at time t; βp is a transformation
exponent relating Z n (t, u) to W n (t, u). P is the cumulative distribution function of the normal
distribution.
Exponential distribution
Exponential distribution is another commonly-used continuous distribution to describe precipitation amount. Its probability density function is a one-parameter function with parameter
29
λe :
f (x) = λe · exp(−λe · x), x, λe 0
(3.18)
Figure 3.5: A variety of exponential distributions with λe
With the specific values of λe , the different shapes of the distributions can be defined. In
Figure 3.5, a set of distributions with different values of λe are presented.
Gamma distribution
Many atmospheric variables are non-symmetrical and skewed to the right, such as precipitation
and wind speed, which are physically constrained to be non-negative. In order to represent
such kind of variables, a variety of distributions that are positively skewed are available. One
of the most commonly used is the gamma distribution. Its probability distribution function
(PDF) is:
f (x) =
(x/β)α−1 · exp(−x/β)
, x, α,β 0
β · Γ(α)
(3.19)
The gamma distribution is a two-parameter distribution. These two parameters are α,
the shape parameter; and β, the scale parameter. Γ(α) is representative of a mathematical
30
function, a gamma function that is a function of the shape parameter α. The density function
of the gamma distribution is not analytically integrable. It has to be obtained by computing
an approximation of its cumulative distribution function by applying an incomplete gamma
function. Therefore, it is relatively computer intensive in comparison to other rainfall generator
functions.
Figure 3.6: A variety of gamma distributions with α and β
The PDF of the gamma distribution possesses a variety of shapes depending on its shape
parameter. For the case α = 1, the gamma distribution is the exponential distribution; for the
case α < 1, the distribution is strongly skewed to the right, the smaller the α, the stronger
the skewness; for the case α > 1, the gamma distribution produces an unimodal shape, the
larger the α, the less the skewness. When α becomes large enough, the gamma distribution approaches an aforementioned distribution, the Gaussian distribution. A variety of combinations
of α and β is presented in Figure 3.6.
3.3.3 Spatial variability of rainfall events
Basics
A rainfall event can be either a local event or regional event. The spatial variability of a rainfall
event is therefore of great importance when studying large-scale flooding events.
31
For the normal distributed variables, the correlation coefficient is a reasonable measure for
estimating the variation of variables. However, the problem arises when dealing with strongly
skewed data with a long-tailed effect, such as precipitation. The normal correlation coefficient
contains several limitations:
- Much more influenced by outliers than by observations near the mean (Lahiri and Moore,
1991). In other words, tailed values strongly affect dependence measures.
- When temporal records of observations are used to estimate the spatial correlation structure, the calculated correlations overestimate the spatial correlation (Gunst, 1995).
There are two possibilities to solve this problem (Journel, 1983): either trim off the highvalued data or smooth out the data by using transfer functions such as logarithms, power
transformation, etc.
In the field of rainfall spatial-temporal structure study, the first option is simply unacceptable
due to the fact that the high-value data contains quite valuable information about rainfall phenomena, especially for the risk analysis, which makes it inappropriate to be ignored. Therefore,
a certain technique is required to describe the regionalization of rainfall, an indicator function
is such a method, it can be expressed as follows in Equation 3.20:
(
1 if z (u) ≤ z
I(u, z) =
0 if not
(3.20)
where z(u) is the measurement at location u, z is the cutoff corresponding to conditional
cumulative distribution. I(u, z) is a binary indicator variable as a function of z with a possible
value of 0 or 1. Corresponding to a given cutoff, the indicator data set changes accordingly.
It can be imagined that there are more 0s when the cutoff is near to the minimum value of z,
and more 1s when it is near to the maximum. At the median, there will be an equal amount
of 0s and 1s.
Here, the cutoff level is selected as 1 mm, which refers to relatively large rainfall events, in
order to deal with rainfall intermittency and to estimate the probability of a day being wet.
Application
The spatial structure of rainfall is presented by a spatial covariance structure Γ0i (t∗ ) and Γ1i (t∗ )
as shown in Equation 3.21 and 3.22, which takes spatial covariance and auto-correlation into
account. Here, Γ0i is the spatial covariance matrix and Γ1i is the space-time covariance for
one-day lag.
Γ0i (t∗ ) = E (W (t) − wi (t∗ )) W T (t) − wiT (t∗ )
32
(3.21)
Γ1i (t∗ ) = E (W (t − 1) − wi (t∗ − 1)) W T (t) − wiT (t∗ )
(3.22)
Their relationship can be linked with an auto-correlation factor r(t∗ ):
Γ1i (t∗ ) = r (t∗ ) Γ0i (t∗ )
(3.23)
The covariance structure is calculated with Equation 3.24, where pi and qi are circulation
pattern dependent and the annual dependent parameters described by the Fourier series. h(x,y)
is the distance between the pair of stations (Stehlik and Bardossy, 2002).
∗)
cov [Wx (t∗ , u), Wy (t∗ , u)] = pi (t∗ )e−h(x,y)qi (t
(3.24)
With the introduction of random numbers ψ(t), precipitation can be generated day by day
using the following generation process:
W (t, u) = r (t∗ ) W (t − 1, u) + Ci (t∗ )ψ (t)
(3.25)
Here, t∗ denotes the Julian day with respect to the consideration of annual impact. r(t∗ ) is
the auto-correlation of a one-day lag to account for the previous day’s impact. Ci (t∗ ) holds for
spatial variability, which is a matrix related to the normal variable W(t,u), according to Bras
and Rodrigues-Iturbe in 1985.
∗ T ∗
Ci (t∗ ) CiT (t∗ ) = Γ0i (t∗ ) − Γ1i (t∗ )Γ−1
0i (t )Γ1i (t )
(3.26)
3.3.4 Parameter estimation
Parameter for precipitation probability
Logistic regression is a commonly used binomial model. The parameters of regression can be
solved using the Newton-Raphson method. It is a method for finding the roots of a complicated
function.
To apply the Newton-Raphson method, an iterative process is often required. Its working
function is expressed as:
0
L (θ)
b = b − 00
L (θ)
∗
(3.27)
0
Where b is a vector of parameters; and b∗ is a vector of true values to be approximated. L (θ)
00
and L (θ) are the first and second derivatives of the log-likelihood function L. Beginning with
the initial vector b, the current estimation is always updated using Equation 3.27 until the
convergence of the algorithm is reached. The vector of parameters is differentiated from station
to station and from CP to CP.
33
Additionally, the maximum likelihood estimator can be selected as a tool to maximize a
log-likelihood with respect to the parameters b0 and b1 .
P (Z > 0) =
1
1 + exp(b0 + b1 x)
(3.28)
The log-likelihood of the logistic regression model is demonstrated using Equation 3.29.
L(b) =
N
X
xTi byi −
i=1
N
X
ni log(1 + exp(xTi b))
(3.29)
i=1
Parameter for precipitation amount distribution
Conventionally, the parameters can be fitted using the simplest method, the moment method.
For example, for a normal distribution, the location parameter µ and shape parameter σ can
be calculated as:
n
1 X
µ= ·
xk
n
(3.30)
k=1
r
σ=
1
· (xk − x)2
n−1
(3.31)
However, the moment method may not be suitable for all of the variables. Thom and Wilks
pointed out that the moments estimator for the gamma distribution is not too bad for larger
values of α, but can be very bad for small values of α. In addition, due to the characteristics of precipitation, the moment estimator may not be efficient to capture the particular
characteristics of its discrete-continuous process. Instead, the distribution parameters can be
estimated by means of a Maximum Likelihood Estimator (MLE). MLE is a method that finds
the value of parameters that make the known likelihood maximized. Through this procedure,
the specific value of the distribution parameters conditioned to each CP can be determined to
locally characterize the behavior of precipitation. The impact of moisture flux is introduced
into the distribution parameters with Equations 3.32 and 3.33, where t∗ stands for the Julian
date corresponding to every actual day; µ0 (t∗ , u) is the expectation of precipitation on the
Julian date presented by the Fourier series. ak and bk are the coefficients of harmonics of
the Fourier series conditioned to CP pattern i. According to harmonic analysis, the Fourier
approximation is able to be identical to the observed time series when (t∗ -1)/2 harmonics are
introduced. Normally, the first 3 harmonics are usually enough.
In the following expressions, Φ and ϕ denote the cumulative distribution and the density
function of normal distribution; µ0 stands for the expectation conditioned to a particular CP;
a represents for the dependence between the daily moisture flux and the precipitation under
34
the influence of a certain CP; MF is the daily moisture flux produced using a NCEP re-analysis
data set; Z0 is the threshold value for the rainfall event.
µ(t, u) = µ0 (t∗ , u) + a · M F (t, u)
(3.32)
K
µ0 (t∗ , u) =
a0 (i, u) X
+
(ak (i, u) cos(kwt∗ ) + bk (i, u) sin(kwt∗ ))
2
(3.33)
k=1
For the skewed normal distribution, MLE is expressed as:
X
−(µ0 (t, u) + a · M F )
n
ln Φ
L (µ0 , σ, a) =
+
σ(t, u)
Z(t,u)≤Z0
X
ln ϕ
Z(t,u)>Z0
Z(t, u)1/β − (µ0 (t, u) + a · M F )
σ(t, u)
!
(3.34)
To apply MLE for solving parameters of exponential distribution, the function has to be
reformatted with a parameter λ, which is the inverse of the expectation of the precipitation.
X
X
Le (λ) =
(λ(t, u) · x) +
(ln λ(t, u) − λ(t, u) · x)
(3.35)
Z(t,u)≤Z0
λ(t, u) =
Z(t,u)>Z0
1
µ0 (t, u) + a · M F
(3.36)
When the gamma distribution is applied, the equation assumes a more complicated form.
X α · Z(t, u)
0
g
L (α, β, µ , a) =
ln γ α, 0
− ln Γ(α) +
µ (t, u)
Z(t,u)≤Z0
!
X
Z(t, u) α−1 Z(t, u)
β
ln
−
− ln
(3.37)
β
β
Γ(α)
Z(t,u)>Z0
Where,
α:
Shape parameter of the gamma distribution
β:
Location parameter of the gamma distribution
0
µ (t, u):
Parameter including the influence of the daily moisture flux into
the distribution’s parameter
0
µ (t, u) =µ0 (t, u) + a · MF (t,u)
The integral of the gamma density function can not be found analytically. It must be
solved by computing approximations of the CDF or from tabulated probabilities. No matter
which option is selected, the variable has to be rescaled to follow the standardized gamma
distribution:
Z(t, u)
ξ=
(3.38)
β(t, u)
After rescaling, the standard variate is dimensionless, and the shape parameter still remains
the same. The cumulative probabilities for the standard gamma distribution can be calculated
through a mathematical function, an incomplete gamma function Γ.
35
Parameter for spatial covariance
As mentioned in Chapter 3.3.3, the spatial structure of rainfall occurrence is calculated with
the indicator correlation. The correlation between the pair of stations k and l is expressed in
general as ρ(k, l). The real-time correlation between the stations is recalculated with ρ(k, l)
defined for the median using the following equation (Abramowitz and Stegun, 1962):
πρ(k, l)
ρr (k, l) = sin
2
(3.39)
3.4 Application to climate change studies
3.4.1 IPCC scenarios
In the year 1992, IPCC released six emissions scenarios providing alternative emissions from
the year 1990 to 2100 for greenhouse-related gases. They are carbon dioxide (CO2 ), carbon
monoxide (CO), methane (CH4 ), nitrous oxide (N2 O), nitrogen oxide (N Ox ), and sulfur dioxide (SO2 ), and are referred to as the IS92 scenarios. These scenarios were initially intended
to be used in the field of atmospheric and climate science for investigating the potential consequences of atmospheric composition and climate change.
They were the first global scenarios to estimate the impact of greenhouse gases. Afterwards,
the IPCC evaluated the IS92 scenarios and found out that weaknesses existed within the
provided scenarios. These weaknesses included the limited range of CO2 , intensities of energy
(CO2 emissions per unit energy) and the absence of any scenario with significant closure to the
income gap between developed and developing countries, even after a full century. In addition,
restructuring in the Eastern Europe and the Former Soviet Union has had far more powerful
effects on economic activity and emissions than were foreseen in the IS92 scenarios. Therefore,
IPCC decided in September 1996 to develop a new set of emissions scenarios, which were
described in the IPCC Special Report on Emission Scenarios, referred to as SRE Scenarios.
These new scenarios cover the wide range of driving forces in the field of demography, technique
and economics that might influence the amounts of greenhouse gases (GHG).
There are four storylines and scenario families that describe the developments in different
economic, technical and environmental fields. The titles of the storylines are A1, A2, B1 and
B2. In the frame of each storyline, there are several more variants with emphasis on different
aspects. The descriptions of each storyline are given as below:
- A1 family describes a world with rapid economic growth during the 21st century and a
substantial reduction in the regional variations of income per head. Global population
rises during the first half of the century, peaks mid-century, and then declines. New and
efficient technology is rapidly introduced.
36
- B1 family describes a world with the same population growth as the A1 family. There
are rapid changes in economic activity away from production towards a service economy. Clean and efficient technologies are introduced. Like A1, this storyline describes a
convergent world.
- A2 family describes a world that remains heterogeneous with a preserved regional identity
and lower income growth per head. The global population rises continuously throughout
the century. The introduction of new and efficient technology is less rapid than in the
other scenarios.
- B2 family describes a world with an increasing population throughout the 21st century,
but at a lower rate than in A2. Levels of economic growth and technological development
are less than those of in A1 and B1.
Up to now, these four storylines and their families have been run by several global circulation models (GCM) throughout the world. These models include CM1 by the Beijing
climate center, CGCM3 by the Canadian Center for Climate Modeling and Analysis, CM3
by the Centre National de Recherches Meteorologiques in France, CSIRO-Mk3.0 by the Commonwealth Scientific and Industrial Research Organization in Australia, ECHAM5-OM by the
Max-Planck-Institute for Meteorology in Germany, CM2.1 by the Geophysical Fluid Dynamics
Laboratory in the United States, HadCM3 by the Met. Office in UK and so on.
Depending on the selected GCM and scenarios, the projection of possible climate images
differ quite a lot. The remarkable difference between two GCM control runs and their corresponding running output for A2 and B2 scenarios can be noticed in Figure 3.7 to Figure
3.10. Climate scenarios are the plausible future climate projection, but are not the real future
climate. The partial original outputs produced by GCMs can be obtained from data distribution centers. Considering the availability of GCM data, the ECHAM4 model developed by the
Max-Planck-Institute for Meteorology in Hamburg, Germany was selected for climate change
impact studies for the following river basins.
3.4.2 Climate scenarios for application
ECHAM is a combination of EC and HAM that stand for the ECMWF atmospheric model and
parameterizations package developed in Hamburg. The model has been evolved continuously,
a summary of developments with respect to physics applied to ECHAM4 is given in Roeckner
et al. in 1996 (Roeckner, 1996).
There have been several experiments run by ECHAM4. The results used here are taken
from the simulations with consideration to the changes of the anthropogenic emissions of CO2 ,
37
Figure 3.7: Monthly precipitation (mm/day) of 2020’s relative to 1961-1990 generated by the
ECHAM4 A2a scenario (IPCC).
ECHAM4 B2a scenario (IPCC).
38
Figure 3.9: Monthly precipitation (mm/day) of 2020’s relative to 1961-1990 generated by the HadCM3
A2a scenario (IPCC).
HadCM3 B2a scenario (IPCC).
39
CH4 , N2 O and SO2 described according to the IPCC defined A2 and B2 scenarios. The model
has been first run with observations considering the greenhouse gas, the direct radiative effect
and the indirect cloud effect of historic sulphate aerosol concentration from 1860 to 1990, and
then run for the next 110 years until 2100.
The gridded daily MSLP, Sh and U-components of the wind field are the predictors of
downscaling process. Applied to climate scenario studies, these variables are derived from
GCM runs for future climate A2 and B2 scenarios instead of that from the NCEP re-analysis
data in the process of the model’s setup. Before being applied to the climate change impact
studies, the variables within the study areas simulated by the GCM are evaluated by the
comparison of the corresponding reanalysis outputs. The investigation is conducted from
season to season. The GCM-simulated value shows similarity with that assimilated by NCEP.
The largest difference in MSLP is up to 6 Pascals, while the smallest is near to -3 Pascals.
As with the MF, there is remarkable difference noticed through the comparison, especially for
West Africa, which is one of the study areas.
Figure 3.11: Average bias of MSLP derived from the ECHAM4 and the NCEP in meter from March
to May.
3.5 Evaluation procedure
3.5.1 Evaluation for CP classification
Circulation patterns are classified based on the daily anomaly of MSLP over the large window
covering the study area. Each day is assigned to a particular CP. As mentioned before, CPs
are optimized using local variables of interests. Therefore, whether the classified CPs are able
to distinguish the weather state in both normal and extreme rainfall events is considered as a
criterion.
40
Figure 3.12: Average bias of MSLP derived from the ECHAM4 and the NCEP in meter from June
to August.
Figure 3.13: Average bias of MSLP derived from the ECHAM4 and the NCEP in meter from September to November.
Figure 3.14: Average bias of MSLP derived from the ECHAM4 and the NCEP in meter from December to Febuary.
41
Figure 3.15: Average bias of MF derived from the ECHAM4 and the NCEP in g.m/kg.s from March
to May.
Figure 3.16: Average bias of MF derived from the ECHAM4 and the NCEP in g.m/kg.s from June
to August.
Figure 3.17: Average bias of MF derived from the ECHAM4 and the NCEP in g.m/kg.s from September to November.
42
Figure 3.18: Average bias of MF derived from the ECHAM4 and the NCEP in g.m/kg.s from December to Febuary.
Iw is a wetness index, calculated with Equation 3.40. It is an overall index for identifying
dependence between the local rainfall events and the governing CPs. It describes the contribution of a certain CP to a regional rainfall amount. The wetness index can be valued as 1,
< 1 and > 1 indicating normal, dry and wet condition respectively. The larger the wetness,
the wetter the CP is, and vice versa. In addition, several statistical indices are calculated as
skill scores to analyze the performance of classified CPs for explaining the variability of precipitation in the given study area from CP to CP as well. They are CP-Frequency, Prec-Mean
and Prec-90, which are calculated for each season, as defined in Table 3.1.
Iw =
Where,
Ri
Ni
(3.40)
i:
CP-id
Ri :
Rainfall contribution in %
Ni :
CP occurrence/frequency in %
Table 3.1: Diagnostics of classified circulation patterns.
Acronym
Definition
Unit
CP-Frequency
Frequency of a particular CP during the study time slice
%
Prec-Mean
Percentage of the observed rainfall events under a given CP
%
Prec-90
Percentage of the rainfall events beyond the 90th percentile
value of the overall precipitation under a given CP
43
%
3.5.2 Evaluation of model performance
The annual cycle of each station is reproduced to ensure the model’s capability of capturing the annual variability of precipitation. In addition to that, the indices representing the
statistics of daily precipitation with consideration to both precipitation occurrence (90N, 90T)
and precipitation amount (P90, Pav, R5D) are selected, apart from those indices reflecting average precipitation (SDI, CDD, Ldd , Lww , Pdd , Pww ). Their definitions are summarized in Table 3.2. Those indices were developed by Malcolm Haylock in STARDEX project
(http://www.cru.uea.ac.uk/cru/projects/stardex/).
Table 3.2: Diagnostics of daily precipitation.
Acronym
Definition
Unit
90N
Total number of events larger than the
90th percentile value of the overall precipitation
90T
%
Percentage of rainfall from events beyond the
90th percentile value of the overall precipitation
%
P90
90th
percentile value of precipitation
mm/day
Pav
Index of the mean precipitation amount
mm/day
SDI
Simple daily intensity (rain per rainy day)
mm/day
CDD
Max no. of consecutive dry days
day
R5D
Greatest 5-day total rainfall
mm
Ldd
Mean dry spell length
day
Lww
Mean wet spell length
day
Pdd
Mean dry-day persistence
day
Pww
Mean wet-day persistence
day
The diagnostics are calculated for each season, each station and each probability distribution.
The inter-annual variability is analyzed with the correlation between the indices calculated from
observed and downscaled daily precipitation time series.
44
4 Application of the CP- and Regression-based
rainfall model
The CP- and Regression-based downscaling model was first developed for downscaling precipitation time series in the Neckar River Basin, Germany, and then transferred to another river
basin characterized with contrasting climate conditions, the Chirchik River Basin, Uzbekistan.
It was expected that the new model could better describe temporal and spatial behavior of
local precipitation in general, and reproduce extreme climate conditions, compared to the pure
regression-based and CP-based downscaling model.
4.1 Application in the Neckar River basin
4.1.1 Study area
The Neckar River, the third largest tributary of the Rhine River, drains a catchment of more
than 14, 000 km2 . It is located in southwestern Germany and its west and south east part
is surrounded by mid-sized mountains (Black Forest, Schwäbische Alb). The waterway of the
Neckar river is about 367 km long and it is intensively used for navigation and transportation,
as well as for energy supply through a number of small water power plants. Approximately,
39% of the total catchment area is forested, 25% is greenland, 25% is used for agriculture
and 10% is settlements. The river basin is located in a temperate climate zone, characterized
as semi-humid and temperate. The average annual precipitation is around 950 mm and the
average daily temperature in the catchment is 8.7 ◦ C with a minimum of 6.4 ◦ C in Klippeneck
(973 m.a.s.l.) and a maximum temperature of 9.1 ◦ C in Nürtingen (280 m.a.s.l.). The coldest
month is January (−0.5 ◦ C in average) , the warmest is July (17.3 ◦ C in average).
The annual precipitation shows a weak seasonality, 60% of the annual precipitation occurs
during the summer term and rest occurs in the winter term, as shown in Figure 4.2. In
general, the highest-amount rainfall occurs in June (110 mm) and the lower rainfall in October
(66 mm). Critical water management problems normally arise in the early spring. Winter
rainfall, together with snow melt upstream of the Neckar, may cause the serious situations
that lead to large areas of floods in the Rhine River.
45
Figure 4.1: Neckar River Basin.
46
1600
Winter
Summer
Annual precipitation [mm]
1400
1200
1000
800
600
400
200
19
60
19
62
19
64
19
66
19
68
19
70
19
72
19
74
19
76
19
78
19
80
19
82
19
84
19
86
19
88
19
90
19
92
19
94
19
96
19
98
20
00
0
Year
Figure 4.2: Annual precipitation amount observed in summer and winter half year in the Neckar River
Basin.
There are 294 precipitation stations distributed in Baden-Württemburg along where the
Neckar river basin lies. 117 of these stations have been collecting long-term observations since
1958 (Figure 4.3). The records from 1958 to 1978 and from 1994 to 1999 are used for the
model’s calibration and rest for the validation.
4.1.2 CP Classification
Identification of critical CP
The circulation patterns classified for the Neckar River basin are generated by MSLP at grid
locations within the Central European window ranging from 65◦ N-15◦ W to 35◦ N-25◦ E. Twelve
distinct CPs are optimally classified by the methodology described in Chapter 3.1. The CPs
are then verified to clearly explain the variability of the precipitation in the study area.
The wetness index, Iw , integrates frequency and amount into one index and is calculated to
analyze the impact of the individual CP on average rainfall events. It is calculated for every
half year and its result is shown in Figure 4.4. The figure explicitly identifies CP04, CP10
and CP11 as wetter CPs in comparison with other CPs, while CP05 and CP08 are drier CPs.
What more, CP11 in particular, appears generally wet in summer but extremely wet in winter;
CP05 appears to be the driest over the whole year. Accordingly, in the following discussion,
CP05 and CP11 are selected as two critical CPs to be studied.
From the anomalies map of CP11 in Figure 4.5, a cyclone can be intuitively identified. A
large area of a low pressure zone is centered over the North Sea and influences the most part
47
Figure 4.3: Distribution of precipitation stations over the Baden-Württemburg.
3.5
3
Wetness index Iw
2.5
2
1.5
1
1
2
3
4
5
6
7
8
9
10
11
12
13
0.5
Summer
Winter
0
CP
Figure 4.4: Wetness index of each CP in summer and winter of the years from 1960 to 1978 and from
1994 to 1999.
48
Figure 4.5: Anomaly maps of pressure distribution for CP05 and CP11.
of western and central Europe. The pressure gradient force decreases from the high-pressure
region to the low-pressure region; wind flows around the cyclone counterclockwise and brings
huge amounts of moisture from the northern Atlantic Ocean. It explains why the heavy rainfall,
especially the large area rainfall, is always produced with the occurrence of this particular CP.
In contrast to CP11, the pressure map of CP05 is a typical anticyclone. The centered high
pressure zone above the most part of western Europe explicitly proves the negative dependence
between the occurrences of CP05 and the local rainfall events.
Apart from that, the statistical analysis of the complete set of CPs shows the same phenomena as the wetness index analysis. The performances of each CP under normal and extreme
conditions in the winter and summer season are tabulated individually in Tables 4.1 and 4.2.
As seen from the tables, CP05 and CP11 show converse behavior from each other in terms of
frequency and contribution to the averaged and extreme rainfall events. With occurrence of
CP11 in winter, 28.4% of the extreme rainfall events are induced despite their low occurrence
rate of 6.2%; however with an occurrence rate as high as 16.9%, only 3.0% of the total extreme
rainfall events were observed under the impact of CP05.
As presented by the above analysis, the classified CP set is proved to be able to clearly
distinguish the main synoptic phenomena using large-scale information. The classified CPs
can be therefore applied as a pre-condition for the stochastic process to determine the rainfall
probability and generate the daily precipitation amount.
Consistence of CP classification
Classification procedure is partly random due to simulated annealing optimization process.
Thus, the obtained parameter sets are “quasi”optimal depending on the objective functions.
Four classifications, from A to D, produced for the Neckar River basin are compared. Classifications A to C are classified using the same input and target variables but have different
sets of random numbers, SA to SD . Classification D uses the same random set as classification
A but with different objective functions. The differences in classifications are summarized in
49
Table 4.1: Statistical analysis of the impact of individual CP on local rainfall events in the winter
[Neckar River basin].
CP
CP-Frequency [%]
Mean [%]
90th [%]
Iw [-]
Iw,extrem [-]
CP01
5.5
5.8
4.3
1.06
0.78
CP02
12.3
7.9
4.0
0.64
0.33
CP03
9.3
5.2
3.0
0.56
0.32
CP04
5.8
12.1
13.9
2.09
2.40
CP05
16.9
6.1
3.0
0.36
0.18
CP06
2.3
2.7
1.6
1.20
0.70
CP07
6.2
4.8
4.6
0.78
0.74
CP08
16.9
7.1
5.6
0.42
0.33
CP09
5.1
3.8
2.6
0.75
0.51
CP10
6.7
12.1
12.9
1.80
1.92
CP11
6.2
17.5
28.4
2.83
4.58
CP12
5
3.3
1.5
0.66
0.30
Table 4.2: Statistical analysis of the impact of individual CP on local rainfall events in summer [Neckar
River basin].
CP
CP-Frequency [%]
Mean [%]
90th [%]
Iw [-]
Iw,extrem [-]
CP01
4.2
5.4
5.5
1.30
1.31
CP02
15.4
6.3
4.3
0.41
0.28
CP03
6.0
6.7
7.4
1.12
1.23
CP04
6.3
12.5
13.5
1.98
2.14
CP05
15.4
5.7
5.5
0.37
0.36
CP06
4.7
3.4
6.1
0.73
1.30
CP07
6.5
5.4
2.0
0.83
0.31
CP08
11.3
5.9
5.9
0.52
0.52
CP09
5.3
4.4
3.2
0.83
0.60
CP10
6.9
14.8
19.1
2.15
2.77
CP11
8.0
15.9
22.7
1.99
2.84
CP12
6.3
5.3
2.4
0.84
0.38
50
Table 4.3.
Table 4.3: Description of different CP classifications.
Classification
Obj. function
Local variable
Input variable
Random
A
Wet+Dry
Sta. precipitation
MSLP (NCEP)
SA
B
Wet+Dry
Sta. precipitation
MSLP (NCEP)
SB
C
Wet+Dry
Sta. precipitation
MSLP (NCEP)
SC
D
Wet
Sta. discharge difference
MSLP (NCEP)
SA
Table 4.4: Contingency table of classification A and classification B based on observed daily precipitation from 1960 to 1990.
CP1a
CP2a
CP3a
CP4a
CP5a
CP6a
CP7a
CP8a
CP9a
CP10a
CP11a
CP12a
CP13a
CP1b
8
318
9
241
227
150
76
348
152
14
119
118
38
CP2b
1
19
78
19
38
122
8
200
262
59
39
124
160
CP3b
92
44
850
23
1
5
155
1
3
21
25
209
0
CP4b
7
31
181
58
3
26
54
125
72
42
35
978
46
CP5b
35
11
61
10
0
8
222
20
4
0
3
284
0
CP6b
14
4
8
136
6
17
10
15
0
76
12
458
0
CP7b
17
331
135
105
50
6
81
3
19
65
115
42
0
CP8b
33
61
91
34
44
24
10
204
143
46
97
123
0
CP9b
952
3
319
7
0
29
27
2
23
3
55
843
0
CP10b
38
34
146
57
14
15
24
34
79
49
74
364
47
CP11b
0
151
0
111
792
15
0
6
38
44
48
0
0
CP12b
0
115
1
291
580
277
2
174
145
417
141
17
209
CP13b
15
0
61
0
0
1
0
0
9
2
28
19
528
A test of independence that assesses whether paired CP classifications are independent of
each other is expressed using a contingency table. The similarities between the first two pairs
of CPs are marked in bold in Tables 4.4 to 4.7. The most dependent pairs are identified and
summarized in Table 4.8. Their pressure anomaly maps are generated in Figures 4.6 to 4.12
for comparison.
Most of the relevant circulation patterns are found to be wet CPs of each CP classification
except the first pair for classification A and D. These wet CPs are all characterized by high
pressure zones centering over western Europe and low pressures zone above the north Atlantic
near to central Europe, which shows a typical cyclone. The exact location of the cyclone is
definitely not the same in each pattern, but is also not far away. The similar CP patterns can
be visualized in Figures 4.6 to 4.12.
Except for the comparison between the anomaly pressure maps, a set of statistical indices introduced in Chapter 3.1.2 is also used to investigate dependencies. The results are summarized
in Tables 4.9 and 4.10.
As expected, the strongest interdependency is obtained between those classifications with
51
Table 4.5: Contingency table of classification A and classification C based on observed daily precipitation from 1960 to 1990.
CP1a
CP2a
CP3a
CP4a
CP5a
CP6a
CP7a
CP8a
CP9a
CP10a
CP11a
CP12a
CP13a
CP1c
0
99
0
151
253
66
0
32
24
52
19
7
0
CP2c
790
34
278
3
0
13
207
6
5
0
35
1227
17
CP3c
0
42
0
90
685
38
0
2
19
71
13
0
0
CP4c
161
10
1117
37
3
22
21
6
25
51
43
405
1
CP5c
8
28
212
132
9
68
74
169
121
93
43
890
60
CP6c
91
38
58
126
56
62
8
6
34
28
67
66
3
CP7c
10
626
58
90
98
5
107
20
12
39
91
7
0
CP8c
1
180
3
26
459
16
0
81
33
37
45
0
1
CP9c
4
9
6
43
89
73
15
59
118
103
155
12
99
CP10c
90
7
138
23
0
12
106
9
9
1
107
489
7
CP11c
5
22
52
255
75
77
10
27
419
183
111
37
0
CP12c
34
24
18
92
17
126
121
715
91
60
56
418
112
CP13c
18
3
0
24
11
117
0
0
39
120
6
21
728
Table 4.6: Contingency table of classification B and classification C based on observed daily precipitation from 1960 to 1990.
CP1b
CP2b
CP3b
CP4b
CP5b
CP6b
CP7b
CP8b
CP9b
CP10b
CP11b
CP12b
CP13b
CP1c
273
14
0
9
0
13
21
5
1
2
122
243
0
CP2c
5
8
352
150
104
272
76
31
1506
70
0
0
41
CP3c
51
34
0
2
0
4
22
8
0
6
438
395
0
CP4c
5
63
858
148
139
28
87
117
293
150
0
4
10
CP5c
59
186
21
1029
51
85
3
50
8
329
4
80
2
CP6c
94
4
5
13
5
45
56
21
133
38
19
184
26
CP7c
266
11
90
13
30
5
505
29
3
34
124
53
0
CP8c
138
4
4
2
0
4
48
144
2
15
424
97
0
CP9c
51
126
0
16
6
36
1
35
16
11
4
461
22
CP10c
33
1
76
75
193
93
42
27
219
191
0
0
48
CP11c
173
226
19
36
13
76
89
178
24
66
67
306
0
CP12c
640
290
4
149
117
84
18
264
41
38
3
221
15
CP13c
30
162
0
16
0
11
1
1
17
25
0
325
499
Table 4.7: Contingency table of classification A and classification D based on observation from 1960
to 1990.
CP1a
CP2a
CP3a
CP4a
CP5a
CP6a
CP7a
CP8a
CP9a
CP10a
CP11a
CP12a
CP13a
CP1d
110
63
156
15
48
11
52
45
28
16
79
237
31
CP2d
43
31
96
183
134
99
16
399
291
229
87
391
169
CP3d
93
138
116
19
31
81
192
146
21
2
43
109
16
CP4d
193
4
99
12
2
15
21
12
11
3
19
593
19
CP5d
10
215
61
327
616
191
52
134
97
164
110
69
287
CP6d
4
6
142
47
9
17
3
56
149
43
26
365
8
CP7d
51
23
34
73
73
19
7
27
51
53
62
249
88
52
CP8d
60
518
58
113
556
37
143
78
57
31
147
157
17
CP9d
3
14
16
79
55
131
28
140
32
14
23
209
45
CP10d
196
18
284
18
1
12
119
10
14
6
29
328
18
CP11d
163
4
551
33
1
11
15
5
23
19
24
564
8
CP12d
48
60
221
94
105
18
5
13
89
127
82
51
5
CP13d
230
14
60
52
81
39
5
31
64
104
49
171
297
Table 4.8: Summary of the most similar CP pairs amongst comparisons of CP classifications.
Class. A-B
Class. A-C
Class. B-C
Class. A-D
Pair I
CP12a - CP04b
CP12a - CP02c
CP09b - CP02c
CP05a - CP05d
Pair II
CP01a - CP09b
CP03a - CP04c
CP04a - CP05c
CP12a - CP04d
Figure 4.6: Anomaly map of CP12a and CP04b.
Figure 4.7: Anomaly map of CP01a and CP09b.
Figure 4.8: Anomaly map of CP12a and CP02c.
53
Figure 4.9: Anomaly map of CP03a and CP04c.
Figure 4.10: Anomaly map of CP09b and CP02c.
Figure 4.11: Anomaly map of CP04b and CP05c.
Figure 4.12: Anomaly map of CP12a and CP04d.
54
Table 4.9: Comparison of CP classifications A to C.
Classification A
Classification B
Classification C
Classification A
-
-
-
Classification B
0.845
-
-
Classification C
0.865
0.862
-
Classification A
-
-
-
Classification B
0.401
-
-
Classification C
0.432
0.427
-
Classification A
-
-
-
Classification B
0.254
-
-
Classification C
0.326
0.345
-
Classification A
-
-
-
Classification B
0.279
-
-
Classification C
0.326
0.329
-
Classification A
-
-
-
Classification B
0.2666
-
-
Classification C
0.3257
0.3369
-
Corr. Pearson coefficient
Cramér coefficient
λa
λb
λsys
Table 4.10: Comparison of CP classifications A to C.
Classification A and Classification D
Corrected Pearson coefficient
0.704
Cramér coefficient
0.265
λa
0.103
λb
0.159
λsys
0.132
55
the same objective function, though the random number sets are completely different. The dependency between two classifications using the different objective function is relatively weaker,
however, still strong. Similar conclusions can be drawn from the λ analysis. These phenomena
reveal facts as (1) consistence remains in the CP classification scheme, although the process
is stochastic; (2) the objective function is quite significant, it must be carefully defined; (3)
either daily precipitation or daily discharge differences can work as a good predictor for CP
classification.
4.1.3 Identification of a dominant atmospheric moisture flux
Surface wind is originally generated by solar convection. It occurs in high or middle latitude
regions in the northern hemisphere where a prevailing surface wind moves from south to north.
Due to the influence of the coriolis force, the wind direction is deflected to the right, namely
prevailing Westerlies. Based on this knowledge, it is assumed that it is the westerly wind that
conveys the moisture that is the major source for the rainfall in the Central Europe.
The assumption can be firstly reflected intuitive by the pressure map for the circulation
patterns. Conditioned to CP11, the wind is obviously coming from the North Atlantic Sector
that is west of the study area. Secondly, the assumption is approved by the regression analysis
related to the dependence on daily precipitation and the daily moisture flux from different
wind directions at various pressure levels.
Figure 4.13: Distribution of rainfall stations within the Neckar River catchment.
The upper atmosphere consists of several pressure layers. Important characteristics of air
56
such as temperature, density, wind velocity, and humidity are different within the given pressure
layers. Here, the variables observed in the pressure layers ranging from 500 hPa to 850 hPa are
selected as candidates to determine the best predictors to reflect the variability of precipitation
in the local region of interest. Apart from that, the stations are divided into 4 groups in relation
to their distances to the center of grid cells used by the NCEP Re-analysis data, as presented
in Figure 4.13. NCEP data at the center of nine neighboring grid cells is used for identifying
the most dominant moisture flux for each rainfall station.
Table 4.11: Average correlation coefficients for the net moisture flux and zonal moisture flux at the
different pressure levels.
500 hPa
700 hPa
850 hPa
Group 1
0.273
0.336
0.330
Westerly MF
Group 2 Group 3
0.315
0.355
0.363
0.426
0.360
0.420
Group 4
0.308
0.358
0.351
Group 1
0.200
0.180
0.167
Southerly MF
Group 2 Group 3
0.169
0.161
0.158
0.151
0.165
0.170
Group 4
0.178
0.163
0.176
Table 4.11 shows the correlations between local rainfall events and the moisture flux at
different pressure levels from 500 hpa to 850 hpa. The results point out that the westerly
moisture flux at 700 hpa has a stronger impact on the local precipitation than the other
combinations and is therefore used as a potential predictor, in addition to MSLP, in rainfall
generating process. Its high correlation coefficient implies the possibility of applying a linear
regression to describe the precipitation amount using the daily moisture flux. In addition, the
impact of CPs and seasonal variability are studied as well. The linear regression model is hence
divided into 3 sub-cases: the unconditional case (MF), the CP dependent case (MF+CP), and
the CP-dependent at annual cycle case (MF+AC+CP). The application of these three sub
models for the calibration and the validation period are presented in Tables 4.12 and 4.13.
Table 4.12: Correlation coefficients between observed precipitation and simulated precipitation using
the CPs classified based on the NCAR and the NCEP data [Calibration].
Calibration
Aver.
STAWB
Max
Min.
MF
0.371
0.059
0.490
0.260
NCAR [5° x 5°]
MF+CP
MF+CP+AC
0.415
0.441
0.060
0.062
0.539
0.574
0.298
0.321
MF
0.225
0.051
0.481
0.338
NCEP[2.5° x 2.5°]
MF+CP
MF+CP+AC
0.421
0.456
0.058
0.059
0.559
0.587
0.310
0.346
Of these three models, the one that takes both the CPs and the annual cycle’s impact
into account induces the best performance. For the calibration and validation period, the
correlation between the observed and simulated daily precipitation reached higher coefficient
57
Table 4.13: Correlation coefficients between observed precipitation and simulated precipitation using
the CPs classified based on the NCAR and the NCEP data [Validation].
NCAR[5° x 5°]
MF+CP
MF+CP+AC
0.454
0.459
0.064
0.072
0.601
0.642
0.336
0.334
Validation
MF
0.409
0.060
0.544
0.292
Aver.
STAWB
Max
Min.
NCEP[2.5° x 2.5°]
MF+CP
MF+CP+AC
0.460
0.466
0.061
0.070
0.596
0.639
0.341
0.319
MF
0.388
0.051
0.537
0.262
(r > 0.45), which obviously shows a better performance than the other two. The outcomes
can be summarized in the following comments:
- The finer the resolution, the stronger the interdependence between precipitation and
moisture flux.
- The models’ performance differs from CP to CP and from season to season.
4.1.4 Determination of rainfall probability
Logistic regression is used to explain the rainfall probability. Figure 4.14, which contains
several CPs, illustrates the interdependence between MF and rainfall probability. The rainfall
probabilities are presented as monotonic increasing curves but differentiated by individual CPs.
Whether a day is wet or dry strongly depends on the MF and the CP appearing on the same
day.
Probability of precipitation [-]
1
CP11
CP02
CP04
CP05
CP08
0.8
CP11
No CP
0.7
0.9
CP02
CP05
0.6
CP04
0.5
0.4
0.3
CP08
0.2
0.1
0
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
Moisture flux [g.m/kg.s]
Figure 4.14: Rainfall probability for the station Sindelfingen conditioned to CPs and MF.
58
As seen in Figure 4.14, the classified circulation patterns successfully differentiate the behavior of rainfall under the impact of the moisture flux. Rainfall probability increases with
the increase of the moisture flux amount, which proves again the proceeding assumption that
more rainfall induced moisture flux comes from the west to the study area. Additionally, the
wet CP always induces the higher rainfall probability compared to the dry one under the same
amount of moisture flux.
- The larger the moisture flux, the higher the probability of precipitation under the same
circulation pattern.
- Given the same amount of MF, the occurrence of wetter CPs always leads to a higher
probability compared to the occurrence of drier CPs.
In order to find out whether the difference between the estimated values and the observed
values is statistically significant, the statistical test has to be performed. Here, the confidence
level is used to construct the intervals with respects to a specified probability of 95%. The
probability of rainfall can be considered simply as the frequency of the weather state being
wet. The weather state is either wet or dry, which fits to the parametric test of the binomial
distribution. The observed weather states are shuffled to calculate the observed frequency of
rainfall for each moisture flux interval conditioned to each CP. The binomial distribution is
then applied to construct its corresponding intervals at a 95% confidence level.
In Figure 4.15, the rainfall probability derived from the observations and the model, together
with the value at the confidence level 95%, are presented. The parameters of the logistic regression model are calculated using the daily moisture flux and the daily precipitation occurring
in the respective CP classes. The observed frequency of rainfall is shown as a discrete variable.
It can be noticed from the figure that the confidence intervals constructed around the plotted
observed frequencies are quite narrow except for the extremely high and low moisture flux. The
calculated probabilities of rainfall using the logistic regression are consistent with the frequencies calculated from the observations. They all fall in the intervals bounded by the confidence
level of 95%. This statistical test indicates that the difference between the estimated values
and observed values is not statistically significant at the 5% level. The result is statistically
acceptable.
The logistic regression is so helpful that the non-linear interdependence amongst CPs, moisture flux and rainfall probability can be integrated into one expression. Consequently, the
daily rainfall probability conditioned to an individual CP is not constant anymore, but varied together with the daily moisture flux, it is able to provide more detailed information for
generating a daily rainfall time series.
59
Figure 4.15: Rainfall probabilities calculated from the observations and logistic regression for CP11
(diamonds: modeled rainfall probability; squares: observed rainfall probability; dashes:
confidence level of 95 %).
The model’s performance is evaluated using split sampling methods. Rainfall generation models with different set-ups were implemented and their outputs were used for evaluating the
influences of coupling the moisture flux to the rainfall probability and the rainfall amount
modules.
The simulated monthly precipitation is first calculated so that it can be compared with
that from the observations. The aim is to evaluate the model’s capability for reproducing
the variability of the annual rainfall at different stations. Several stations that are evenly
distributed in the study area were selected for demonstrating the model’s performances. They
are summarized in Tables 4.14 and 4.15. It can be concluded that all these models that are
coupled with the moisture flux are able to represent the annual cycle of rainfall much better
in comparison with the one without moisture flux. It implies the impact of the moisture flux
on the local precipitation phenomenon.
The temporal variation of monthly precipitation is presented by data collected at several
stations, as shown in Figures 4.16 and 4.17. Amongst models coupling with the moisture flux,
the models setup with the normal and exponential distributions perform more reliably than
that with gamma distribution. In terms of the bias caused by the models, the model using
the skewed normal distribution causes the least bias, 0.9 mm/month during the winter half
year and -0.09 mm/month in the summer half year, while the one with gamma distribution
produces much more bias that greatly overestimates the precipitation in both the winter and
60
Table 4.14: Correlation coefficients between monthly precipitations derived from observed and simulated daily precipitation [Calibration].
CP
(normal
distribution)
CP+MF
(normal
distribution)
CP+MF
(exponential
distribution)
CP+MF
(Gamma
distribution)
FREUDENSTADT (WST)
0.67
0.91
0.77
0.71
ALBSTADT BURGFELDEN
0.92
0.98
0.99
0.98
0.88
0.98
0.97
0.95
0.94
0.97
0.96
0.91
0.97
0.98
0.98
0.97
0.56
0.90
0.79
0.70
0.72
0.86
0.94
0.84
ABTSGMUEND
0.77
0.89
0.93
0.87
STOETTEN (WST)
0.89
0.96
0.97
0.94
PLEIDELSHEIM
0.86
0.93
0.96
0.91
ADELSHEIM
0.63
0.83
0.81
0.48
WALDENBURG
OBERSTEINBACH
0.66
0.90
0.89
0.86
MANNHEIM (WST)
0.87
0.89
0.97
0.88
EPPINGEN ELSENZ
0.72
0.90
0.94
0.87
TIEFENBRONN
0.77
0.93
0.94
0.84
ALTENSTEIG WART
0.67
0.92
0.86
0.80
Stations
ROTTENBURG
NIEDERNAU,BAD
VILLINGEN
SCHWENN.(NST)
ESSLINGEN/NECKAR
WALDBRUNN
OBERDIELBACH
FRANKENHARDT
GRUENDELH.
61
Table 4.15: Correlation coefficients between monthly precipitations derived from observed and simulated daily precipitation [Validation].
CP
(normal
distribution)
CP+MF
(normal
distribution)
CP+MF
(exponential
distribution)
CP+MF
(Gamma
distribution)
FREUDENSTADT (WST)
0.76
0.96
0.83
0.84
ALBSTADT BURGFELDEN
0.83
0.92
0.89
0.84
0.83
0.77
0.83
0.91
0.80
0.84
0.79
0.80
0.95
0.92
0.95
0.96
0.80
0.93
0.79
0.65
0.67
0.90
0.83
0.67
ABTSGMUEND
0.66
0.84
0.75
0.72
STOETTEN (WST)
0.66
0.87
0.87
0.77
PLEIDELSHEIM
0.77
0.87
0.79
0.71
ADELSHEIM
0.73
0.84
0.80
0.30
WALDENBURG
OBERSTEINBACH
0.71
0.87
0.82
0.61
MANNHEIM (WST)
0.70
0.60
0.71
0.68
EPPINGEN ELSENZ
0.67
0.79
0.63
0.58
TIEFENBRONN
0.73
0.82
0.73
0.74
ALTENSTEIG WART
0.55
0.65
0.58
0.36
Stations
ROTTENBURG
NIEDERNAU,BAD
VILLINGEN
SCHWENN.(NST)
ESSLINGEN/NECKAR
WALDBRUNN
OBERDIELBACH
FRANKENHARDT
GRUENDELH.
62
summer half year, especially for the summer half year.
VILLINGEN SCHWENN. (NST)
140
Observed
Normal distribution (No MF)
Gamma distribution
Normal distribution
Monthly precipitation [mm]
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ALBSTADT BURGFELDEN
140
Observed
Normal distribution
Gamma distribution
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
FREUDENSTADT (WST)
300
Observed
Normal distribution
Gamma distribution
250
200
150
100
50
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
Figure 4.16: Annual cycle of precipitation at stations in the catchment area during validation [continued].
In addition, a few of the extreme-related indices and conventional indices are calculated
seasonally for each station to study the inter-annual variability of precipitation from year to
year. The indices are derived individually from the simulated and the observed time series of
precipitation data and their correlation is used as a measure to evaluate the model’s performance. The results calculated for the winter and summer seasons are shown in a bar chart in
Figures 4.18 and 4.19. Each bar represents an individual model setting. The first and second
63
FRANKENHARDT GRUENDELH.
140
Observed
Normal distribution
Gamma distribution
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ABTSGMUEND
180
Observed
Normal distribution
Gamma distribution
160
140
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ESSLINGEN/NECKAR
140
Observed
Normal distribution
Gamma distribution
120
100
80
60
40
20
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
Figure 4.17: Annual cycle of precipitation at stations in the catchment area during validation.
64
Spring
0.80
No MF
Skewed normal distribution+MF
Exponential+MF
Gamma distribution+MF
0.70
0.60
Correlation [-]
0.50
0.40
0.30
0.20
0.10
0.00
90N
90T
P90
Pav
SDI
CDD
R5D
P50
Ldd
Lww
Pdd
Pww
-0.10
Diagnostic indice
Summer
0.65
No MF
Exponential+MF
0.55
Correlation [-]
0.45
0.35
0.25
0.15
0.05
-0.05
90N
90T
P90
Pav
SDI
CDD
R5D
P50
Ldd
Lww
Pdd
Pww
Diagnostic indice
Figure 4.18: Averaged extreme indices over the whole river basin for the spring and the summer
seasons [Validation].
65
Autumn
0.80
No MF
0.70
Exponential+MF
Correlation [-]
0.60
0.50
0.40
0.30
0.20
0.10
0.00
90N
90T
P90
Pav
SDI
CDD
R5D
P50
Ldd
Lww
Pdd
Pww
Diagnostic indice
Winter
0.70
No MF
Exponential+MF
0.60
Correlation [-]
0.50
0.40
0.30
0.20
0.10
0.00
90N
90T
P90
Pav
SDI
CDD
R5D
P50
Ldd
Lww
Pdd
Pww
-0.10
Diagnostic indice
Figure 4.19: Averaged extreme indices over the whole river basin for the autumn and the winter
seasons [Validation].
66
models stand for the performance derived from generators using skewed normal distribution;
the proceeding one with no moisture flux and the latter one with a moisture flux. The weather
state of being wet or dry is controlled by the random variable of the distribution. Precipitation
is generated only when the random variable is greater than zero, otherwise the precipitation on
that day is recorded as zero. The last two models represent the performance of the generator
using the exponential distribution and the gamma distribution respectively. Both of them are
set up with consideration to the moisture flux. Precipitation is generated when the random
variable is larger than the rainfall probability, as determined by the logistic regression.
The results from all three models come to the common conclusion that precipitation generators work quite well to reproduce the inter-annual variability of precipitation. In winter,
all of the models that are coupled with moisture flux clearly show a greater improvement
in terms of indices related to both mean precipitation and extreme precipitation conditions.
Especially for the model using the skewed normal distribution, the ability to reproduce the
inter-annual variability has been enhanced by 100%. The models with exponential distributions and gamma distributions do not perform as well as the model using the skewed normal
distribution; nevertheless, they produce a better result than the model without the moisture
flux. This implies the importance of introducing the continuous meteorological predictors in
addition to the discrete circulation patterns when generating the meteorological variables. In
summer, the capabilities of the models for reproducing the inter-annual variability were still
improved, however, not as much as for that in the winter. The model with the exponential
distribution shows the best performance for all three model set-ups. The ability for presenting
the extreme rainfall events is increased by 25% and for the normal rainfall events by 60%;
however, the models’ performances are in general quite weak.
4.1.6 Climate scenarios
Precipitation-related circulation patterns for future scenarios are derived from the mean sea
level pressure, produced by the ECHAM4 model. The patterns are similar to those derived
from NCEP for the current climate conditions. The frequency and persistence of a particular
CP during the long-term situations are calculated to determine the difference between the CP
sequences derived from NCEP re-analysis data and those from ECHAM4 data. In addition,
the performance of CPs under A2 and B2 scenarios are compared to the under control runs
in order to evaluate the impact of climate change. Tables 4.16 to 4.21 show the expectation
of the aforementioned statistical analysis for CP05 (dry) and CP11 (wet). These CPs were
derived respectively from reanalysis data and GCM control runs, A2 and B2 scenarios.
In the frequency studies, both dry and wet CPs are generally overestimated by the GCMs
control runs [CTL] in comparison to the NCEP reanalysis model, except for CP11 in winter.
67
Table 4.16: Frequency of critical CPs in winter and summer over a long-term time period [%].
CP11
CP05
NCEP
8.83
14.96
Winter
CTL
A2
9.55
9.25
16.4
18.0
B2
9.10
15.8
NCEP
9.00
13.00
Summer
CTL
A2
8.34
9.80
14.6
13.76
B2
9.80
13.0
Table 4.17: Frequency of critical CPs in spring and autumn over a long-term time period [%].
CP11
CP05
NCEP
8.30
14.00
Spring
CTL
A2
9.00
8.30
14.2
16.5
B2
8.8
15.1
NCEP
8.16
15.00
Autumn
CTL
A2
10.7
10.0
15.3
16.0
B2
10.4
16.7
Table 4.18: Mean persistence of critical CPs in winter and summer a over long-term time period [day].
CP11
CP05
NCEP
1.75
1.96
Winter
CTL
A2
1.56
1.44
1.84
1.95
B2
1.37
1.91
NCEP
1.40
1.85
Summer
CTL
A2
1.31
1.43
1.73
1.76
B2
1.44
1.63
Table 4.19: Mean persistence of critical CPs in spring and autumn over a long-term time period [day].
CP11
CP05
NCEP
1.56
1.81
Spring
CTL
A2
1.42
1.37
1.90
1.87
B2
1.37
1.92
NCEP
1.54
1.79
Autumn
CTL
A2
1.45
1.45
1.89
1.86
B2
1.38
1.83
Table 4.20: Maximum persistence of critical CP in winter and summer over a long-term time period
[day].
CP11
CP05
NCEP
7
9
Winter
CTL
A2
5
6
9
16
B2
5
11
NCEP
5
11
Summer
CTL
A2
4
4
7
7
B2
4
6
Table 4.21: Maximum persistence of critical CP in spring and autumn over a long-term time period
[day].
CP11
CP05
NCEP
7
12
Spring
CTL
A2
9
5
8
8
B2
5
8
68
NCEP
9
7
Autumn
CTL
A2
5
4
9
7
B2
4
8
The differences change from season to season and most of them vary in the range of ±10%,
except for CP11 in the autumn. As to the persistency analysis, the opposite trend is identified.
The difference is about 6% in terms of the mean persistency of dry and wet CPs, however, the
difference in maximum persistency is quite significant.
Apart from CPs, the moisture flux is another important predictor in rainfall generation. As
presented in Figures 3.15 to 3.18, the differences between the NCEP moisture flux and the
ECHAM4 moisture flux can be identified in different seasons. In winter, similar to that in
autumn, the moisture flux is generally underestimated by the ECHAM4 above central Europe.
However, in autumn, the underestimated moisture flux center is more shifted in the southwestern direction. In spring and summer, the opposite situation is noticed. The moisture flux
derived from the ECHAM4 control runs is generally overestimated by 4-8 g/kg*m/s in those
regions above the central Europe.
Monthly averaged precipitation [mm]
120
100
80
60
40
Obs.(1961-1978;1994-2000)
Simulated(1961-1978;1994-2000)
20
ECHAM4-A2
ECHAM4-B2
0
1
2
3
4
5
6
7
8
9
10
11
12
Month
Figure 4.20: Annual monthly precipitation at Esslingen under the impact of climate change.
Reflected in data from individual local stations, for instance at Esslingen, the climate change
shows significant impact namely in winter and autumn up to the year 2030. As shown in Figure
4.20, both A2 and B2 scenarios indicate a similar trend that there can be a great increase of
monthly precipitation in the autumn and winter, whereas there is decrease during the summer.
69
4.2 Application in the Chirchik-Ahangran River Basin
4.2.1 Study area
Description of the river basin
The Chirchik - Ahangaran basin, as shown in Figure 4.21, is located in the north-eastern part
of the Republic of Uzbekistan in central Asia, between the Syrdarya River and the western
Tien Shan Mountains. The whole river basin stretches out within the area of three republics,
Kazakhstan, Kyrgyzstan, and Uzbekistan, but mainly located in the Republic of Uzbekistan.
Figure 4.21: River network and gauge stations within the Chirchik River Basin.
The river basin can be viewed as two parts: the upper Chirchik and the lower Chirchik. The
upper Chirchik lies in the north-eastern mountainous area with natural hydrological conditions,
whereas the lower Chirchik in the south-western part is characterized by flat plains and many
artificial hydraulic structures for agriculture purposes.
The whole basin is located in a continental, sub-tropical climate zone, where the cyclone
and anticyclones formed above the continents at higher latitude regions are the major driving
forces for the synoptic climate. Five exemplary stations are chosen to demonstrate the local
meteorological condition in terms of precipitation and average temperature. These five stations
are Oygaing, Pskem, Tashkent, Dukant and Angren. Oygaing and Pskem are located in northeastern mountainous areas and the others are located in the south-western plain area.
As seen in Figure 4.22, the peak rainfall generally occurs in the early spring, while the
amounts of rainfall during the summer months are quite small. Under serious conditions,
the rainfall amount is close to zero. Local precipitation is distributed quite unevenly. More
70
Figure 4.22: Monthly rainfall amounts observed at the stations of Oygaing, Pskem, Tashkent, Dukant
and Angren, distributed from north to south.
precipitation occurs in the northern and western parts of the region due to a westerly wind
conveying more moisture flux.
Similar to the other regions in the subtropical climate zones in the northern hemisphere,
the temperature in the Chirchik-Ahangaran basin changes distinctly from season to season,
see Figure 4.23. Summer is the hottest season of the whole year, especially for the plain; the
temperature is normally hotter in the plain than in the mountainous areas. On the plain, the
average temperature is more than 25 ◦ C and the maximum temperature can reach 40 ◦ C. In
winter, the areas on the plain are warmer than in the mountains. The average temperature
can be as low as −10 ◦ C in the mountains compared with 2 ◦ C on the plain.
Data availability
There are several ground-based meteorological stations located in the study area, however, only
a few of them at daily temporal resolution are accessible to us. Most of the meteorological
stations have records from the 1950’s to the year 1991 and from the year 2000 to present. The
length of the observations is quite limited and even within the observation period there are
many missing values.
The limited observation records were collected from different data resources. The time slices
and temporal resolution are summarized in Table 4.23 to 4.24:
As was done with the Neckar River Basin, large-scale meteorological parameters are derived from NCEP re-analysis archives. MSLP serves as a predictor for the classification of
71
30
Oygaing
Pskem
25
Monthly average temperature [°C]
Tashkent
Dukant
20
Angren
15
10
5
0
1
2
3
4
5
6
7
8
9
10
11
12
-5
-10
-15
Month
Figure 4.23: Monthly average temperature observed at the stations of Oygaing, Pskem, Tashkent,
Dukant and Angren, distributed from North to South.
Table 4.22: Meteorological data provided by Hydromet in Uzbekistan (1980-2003).
Station ID
Prec.
Tmax/Tmin
Pressure
Humidity
Wind
Temporal resolution
Angren
+
+
+
+
+
Monthly (1980-2003)
Dukant
+
+
+
+
+
Monthly (1980-2003)
Oygaing
+
+
+
+
+
Monthly (1980-2003)
Pskem
+
+
+
+
+
Monthly (1980-2003)
Tashkent
+
+
+
+
+
Monthly (1980-2003)
72
Table 4.23: Meteorological data obtained from Global Daily Climatology Network (KNMI).
Station ID
Prec.
Tmax/Tmin
Completeness
Temporal resolution
Tashkent
+
+
good
Daily (1891-1991)
Dukant
+
-
poor
Daily (1959-1991)
Oygaing
+
-
poor
Daily (1962-1991)
Pskem
+
-
fair
Daily (1936-1991)
Kamchik
+
-
poor
Daily (2000-2004)
Kizil’cha
+
-
poor
Daily (1958-1991)
Charvak
+
-
fair
Daily (1936-1991)
Kauncy
+
-
poor
Daily (1959-1991)
Paca-ata (Kyrgyzstan)
+
-
fair
Daily (1914-1991)
Urtatoky (Kyrgyzstan)
+
-
fair
Daily (1959-1987)
Table 4.24: Meteorological data obtained from Russian’s weather server.
Station ID
Prec.
Tmax/Tmin
Temporal resolution
Angren
+
+
Daily (2000-2004)
Dukant
+
+
Daily (2000-2004)
Oygaing
+
+
Daily (2000-2004)
Pskem
+
+
Daily (2000-2004)
Tashkent
+
+
Daily (2000-2004)
Bekabad
+
+
Daily (2000-2004)
Chimgan
+
+
Daily (2000-2004)
Kamchik
+
+
Daily (2000-2004)
73
precipitation circulation patterns above the central Asia region. The product of extracted
geotropic wind and specific humidity is applied as a potential predictor to enhance the model’s
performance.
4.2.2 Identification of circulation patterns
From a statistical point of view, time series of observations should be as long as possible in order
to capture all of the local meteorological phenomena. Constrained by the data availability, the
station Tashkent is the only station that contains the long-term continuous measurements in
terms of both precipitation and temperature. Its daily precipitation data is hence used as the
local variables for optimizing precipitation circulation patterns (CPs).
The classified circulation patterns consists of a total of 12 types, some of which dominate
the specific climate conditions. The anomaly pressure maps of individual CPs are presented in
Figures 4.24 and 4.25. The behavior of local rainfall events in relation to the governing CPs is
identified using the index “Wetness”. Similar to the analysis done for the Neckar CPs, several
statistical indices are defined and calculated to compare the contribution of the CPs to the
rainfall in each season. The results, together with the wetness index Iw , calculated for each
season are presented in Tables 4.26 to 4.29.
The anomaly pressure maps of different circulation patterns are generated and the mechanisms behind them are studied. Of the 12 circulation patterns, CP08 and CP11 can be
recognized as wet CPs no matter whether in the winter or summer, whereas CP02, CP03 and
CP10 are quite dry. Under the impact of CP08 and CP11, the low pressure zones presides
cover the most part of Kyrgyzstan and Tadzhikistan and the western range of the Tiangshan
Mountains, and therefore cause a high amount of rainfall. Both CPs occur with relatively
low frequencies, nevertheless, they contribute to the larger rainfall events, especially in the
extreme cases. In contrast to “wet CPs”, the anomaly maps of CP02 and CP10 indicate the
characteristics of an anticyclone. They occur frequently, but their contribution to the rainfall
processes is very limited due to the high pressure zone dominating regions.
Different from the application of CPs for the Neckar River Basin, the classified CPs are
required to be regrouped to deal with the frequently occurring dry spells during June and
July. Several classified circulation patterns are seldom observed in the time period over the
study area; this makes it difficult to obtain enough original data and to further identify the
reliable statistical relationship between CPs and precipitation for a single CP. The contribution
of a single CP to rainfall events is chosen as a criterion to reclassify the CPs. Thereafter,
the variability of precipitation conditioned to each group of CPs is captured by distribution
functions, and daily precipitation is generated stochastically, together with consideration of the
spatial correlation amongst the different stations and auto-correlation at each single station.
74
Figure 4.24: Anomaly pressure maps of circulation patterns classified for the Chirchik River basin:
CP01-CP06.
75
Figure 4.25: Anomaly pressure maps of circulation patterns classified for the Chirchik River basin:
CP07-CP12.
76
Table 4.25: Statistical analysis of the impact of individual CPs on local rainfall events in spring
[Chirchik River Basin].
CP
CP-Frequency [%]
Mean[%]
90[%]
Iw [-]
Iw,extrem [-]
CP01
5.1
3.0
3.5
0.59
0.69
CP02
13.5
5.1
3.5
0.38
0.26
CP03
4.4
2.0
0.3
0.45
0.07
CP04
12.6
11.6
6.7
0.53
0.53
CP05
5.3
4.2
3.7
0.79
0.70
CP06
4.0
8.2
7.8
2.05
1.95
CP07
3.8
4.8
5.3
1.26
1.39
CP08
5.9
14.1
23.2
2.39
3.93
CP09
10.7
9.4
8.8
0.88
0.82
CP10
8.6
5.2
3.9
0.60
0.45
CP11
6.9
17.3
28.9
2.51
4.19
CP12
7.5
7.0
2.3
0.93
0.31
Table 4.26: Statistical analysis of the impact of individual CPs on local rainfall events in summer
CP
CP-Frequency [%]
Mean[%]
90[%]
Iw [-]
Iw,extrem [-]
CP01
7.4
5.9
5.9
0.80
0.80
CP02
13.4
1.8
0.0
0.13
0.00
CP03
5.9
6.4
7.4
1.08
1.25
CP04
13.1
11.9
7.6
0.91
0.58
CP05
7.8
10.7
5.6
1.37
0.72
CP06
3.3
4.3
4.5
1.30
1.36
CP07
4.2
6.8
8.3
1.62
1.98
CP08
3.5
18.5
48.0
5.29
13.7
CP09
12.6
6.7
1.1
0.53
0.09
CP10
8.1
5.2
2.8
0.64
0.35
CP11
3.9
9.7
4.5
2.49
1.15
CP12
7.3
4.8
2.5
0.66
0.34
77
Table 4.27: Statistical analysis of the impact of individual CPs on local rainfall events in autumn
CP
CP-Frequency [%]
Mean[%]
90[%]
Iw [-]
Iw,extrem [-]
CP01
5.2
4.5
3.9
0.87
0.75
CP02
15.9
3.1
1.0
0.19
0.06
CP03
5.0
0.9
1.6
0.18
0.32
CP04
13.3
14.5
7.0
1.09
0.53
CP05
5.9
3.4
1.4
0.58
0.24
CP06
3.1
7.7
12.3
2.48
3.97
CP07
3.2
2.4
5.5
0.75
1.72
CP08
4.4
12.2
20.5
2.77
4.66
CP09
10.2
7.4
1.4
0.73
0.14
CP10
7.5
2.3
0.0
0.30
0.00
CP11
5.8
22.7
33.9
3.91
5.84
CP12
8.5
7.4
3.3
0.87
0.39
Table 4.28: Statistical analysis of the impact of individual CPs on local rainfall events in winter
CP
CP-Frequency [%]
Mean[%]
90[%]
Iw [-]
Iw,extrem [-]
CP01
3.6
4.3
1.4
1.19
0.39
CP02
14.8
3.1
0.4
0.21
0.03
CP03
4.4
2.9
2.3
0.66
0.52
CP04
14.6
14.8
19.6
1.01
1.34
CP05
7.1
3.2
0.8
0.45
0.13
CP06
4.3
10.5
11.1
2.44
2.58
CP07
4.0
4.4
3.3
1.10
0.83
CP08
3.4
6.3
11.0
1.85
3.24
CP09
9.0
6.4
2.6
0.71
0.29
CP10
8.3
5.9
2.5
0.71
0.30
CP11
8.4
21.0
32.2
2.50
3.83
CP12
7.6
6.7
5.7
0.88
0.75
78
4.2.3 Identification of atmospheric moisture flux on rainfall
Again, the daily moisture flux is considered as a potential predictor that has been proved to
have a dominant impact on the rainfall process in the Neckar River Basin.
Specific for the Chirchik River Basin, the moisture flux (MF) may be conveyed by wind
from the Atlantic Ocean from the west, the Barents Sea from north and the Arabian Sea from
the south. MF-related variables at the pressure levels 700 and 850 are studied. It turns out
that the westerly MF at 700 hpa also plays an important role for the local rainfall events, as
compared with other working forces. The results are summarized in Table 4.30.
Table 4.29: Correlation coefficients between moisture flux and rainfall events in winter [Chirchik River
Basin].
Zonal
Meridional
Zonal
Meridional
(700hpa)
(700hpa)
(850hpa)
(850hpa)
Charvak
0.48
0.35
0.42
0.25
Pskem
0.53
0.39
0.43
0.26
Tashkent
0.36
0.27
0.30
0.21
Dukant
0.44
0.31
0.40
0.25
Kizil’cha
0.47
0.31
0.41
0.23
Tuaybuguz
0.36
0.31
0.35
0.26
U st0 E
0.31
0.19
0.25
0.17
P .ters
4.2.4 Determination of rainfall probability
Logistic regression is applied to explain the rainfall probability of the different circulation
patterns. Figure 4.26 presents the evolution of precipitation probabilities with the aid of a
daily moisture flux under the impact of a wet CP, CP11 and a dry CP, CP02.
The same phenomenon as that for the Neckar River basin is observed. Both CPs and the
daily moisture flux are quite dominant for determining the rainfall probability: the larger
the moisture flux, the higher the probability of rainfall; the wetter the CP, the higher the
probability the day is likely to be wet. According to the CP that occurred on the studied
day, the corresponding probability of the day being wet can be completely different due to the
impact of the CP and of the moisture contained in the air.
In Figure 4.27, the observed and estimated rainfall probabilities are presented, together
with a confidence level of 95%. It shows the ability of using logistic regression to reproduce the
probabilities. Whether the difference between the estimated and observed values is statistically
79
1
0.9
Probability of precipitation [-]
0.8
CP11
0.7
0.6
CP02
0.5
0.4
0.3
0.2
All CP
0.1
0
-0.06
-0.04
-0.02
0
0.02
0.04
0.06
0.08
0.1
Moisture flux [g.m/kg.s]
Probability
Figure 4.26: Rainfall probability for the station Tashkent conditioned to CPs and MF.
Figure 4.27: Rainfall probabilities calculated from the observations and logistic regression for CP11
(diamonds: modeled rainfall probability; squares: observed rainfall probability; dashes:
confidence level of 95 %).
80
significant must still be analyzed. The same procedures and confidence level as described in
Chapter 4.1.4 are applied.
It can be noticed, that the confidence intervals constructed around the observed frequencies
is quite narrow except the extremely high moisture flux. The calculated probabilities of rainfall
using logistic regression are consist with the frequencies calculated from the observations. They
all fall in the intervals bounded by a confidence level of 95%. This statistical test indicates that
the difference between the estimated values and observed values is not statistically significant
at the 5% level. The resultant logistic regression is statistically acceptable to represent rainfall
probability.
Five stations containing relatively long observation time series are selected for the precipitation
downscaling. These five stations are Pskem, Charvak, Tashkent, Olgaing and Dukant, located
in the upper chirchik, lower chirchik and in the mountains area respectively. Due to a limitation
of data availability, daily time series measured at these stations from the year 1960 to 1976 are
used for the model’s calibration and the monthly rainfall amount for the other years provided
by the Hydromet in Uzbekistan are used for the validation.
Two models incorporated with moisture flux are implemented here, one is presented with a
skewed normal distribution and the other is presented with an exponential distribution.
5.0
Monthly precipitation [mm/day]
Observed
4.5
Normal + MF
4.0
Exponential + MF
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
Figure 4.28: Annual cycle of monthly precipitation derived from observation and simulation out of 2
model settings during calibration [Station: Charvak].
81
4.5
Observed
4.0
Normal + MF
Exponential + MF
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
model settings during calibration [Station: Pskem].
4.0
Observed
Normal + MF
3.5
Exponential + MF
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
model settings during calibration [Station: Olgaing].
82
3.0
Observed
Normal + MF
2.5
Exponential + MF
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
model settings during calibration [Station: Tashkent].
5.0
Observation
4.5
Exponential + MF
4.0
Normal + MF
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
model settings during calibration [Station: Dukant].
83
The output of both model set-ups was successful in capturing the monthly precipitation
amount over a long period of time. All the simulations are able to reproduce the occurrence of
peak rainfalls in the early spring, mostly in March and April, which is differentiated between
the plain and mountainous areas from station to station. The model setup with an exponential
distribution shows a better fit than that with the skewed normal distribution. There is however, still the bias between monthly precipitation derived from observation and simulations,
especially at the beginning of the year.
As well as the long-term mean being quite important, the model’s performance under extreme conditions is also of great interest. Therefore, the model’s capability of representing
inter-annual variability is also under evaluation using precipitation-related indices, as listed in
Tables 4.31 and 4.32.
Winter
Bias
CP
Pav
90N
P90
Correlation
Bias
Correlation
Aver
Max
Aver
Aver
Max
Aver
0.24
0.45
0.17
0.18
0.47
0.15
CP +
MF1
0.41
0.53
0.32
0.14
0.60
0.31
CP +
MF2
0.35
0.75
0.48
0.13
0.60
0.35
CP
90T
Summer
0.03
0.32
0.02
0.05
0.30
0.04
MF1
0.04
0.38
0.09
0.05
0.37
0.06
CP + MF2
0.03
0.37
0.07
0.05
0.37
0.07
CP
0.32
0.36
0.12
0.20
0.32
0.05
CP + MF1
0.42
0.44
0.17
0.16
0.45
0.11
CP + MF2
0.28
0.50
0.21
0.20
0.42
0.15
CP
CP +
2.19
0.34
0.02
2.95
0.48
-0.01
CP +
MF1
2.48
0.40
0.12
3.08
0.34
-0.07
CP +
MF2
2.86
0.52
0.13
3.22
0.59
0.15
Table 4.30: Precipitation related diagnostic analysis in winter and summer.[1 Skewed normal distribution with moisture flux;
2
Exponential distribution with moisture flux]
The models perform well with respect to average precipitation in most seasons even in the
summer. The average correlation between simulated and observed precipitation reaches the
highest value of 0.53 in the spring and the lowest value of 0.35 in the summer. For the other
indices, the average correlation is not as high as Pav, but still reaches an acceptable level for
extreme value analysis. However, the model is quite weak in representing the percentage of
total rainfall of events whose amount is higher than the long-term 90th percentile.
Generally speaking, the model is able to describe inter-annual variability of precipitation at
84
Spring
Bias
CP
Pav
90T
90N
Correlation
Bias
Correlation
Aver
Max
Aver
Aver
Max
Aver
0.21
0.44
0.17
0.16
0.48
0.12
CP +
MF1
0.20
0.63
0.41
0.15
0.64
0.29
CP +
MF2
0.31
0.72
0.53
0.14
0.65
0.43
CP
0.03
0.32
0.03
0.06
0.38
0.06
CP + MF1
0.03
0.46
0.12
0.06
0.34
0.05
CP + MF2
0.03
0.37
0.08
0.05
0.35
0.04
CP
0.32
0.38
0.05
0.22
0.40
0.06
CP + MF1
0.33
0.49
0.22
0.21
0.45
0.15
MF2
0.24
0.54
0.25
0.21
0.50
0.21
CP +
CP
P90
Autumn
1.31
0.45
0.09
2.76
0.47
-0.03
CP +
MF1
1.39
0.45
0.17
1.80
0.48
0.08
CP +
MF2
2.33
0.45
0.17
2.60
0.62
0.12
Table 4.31: Precipitation related diagnostic analysis in spring and autumn.[1 Skewed normal distribution with moisture flux;
2
Exponential distribution with moisture flux]
a seasonal scale. All indices achieve the highest correlation in spring, even for extreme indices,
followed by the winter, autumn and summer. Compared with the skewed normal distribution,
the setting with an exponential distribution is better, especially under extremes. Therefore,
the further downscaling will adopt an exponential distribution to describe precipitation time
series.
To study climate condition under the impact of climate change, the large-scale parameters derived from the A2 and B2 scenarios provided by global circulation models (GCMs), ECHAM4,
are downscaled for the target region for the first 30 years of the current century, from the year
2000 to 2030. The model’s output from the control run is used to evaluate the predictor used
for the downscaling process, and its output conditioned to the A2 and B2 scenarios are used
for the downscaling of daily precipitation.
The circulation patterns for precipitation and temperature for the time period up to the
year 2030 are derived from mean sea level pressure from the ECHAM4 output. The mean
seasonal frequency and mean persistence of specific precipitation CPs are compared between
NCEP derived CPs and ECHAM4 derived CPs, see Tables 4.33 to 4.38.
In addition, the uncertainty of the moisture flux derived from the global model is also under
85
Table 4.32: Frequency of wet CPs in winter and summer [%].
CP08
CP02
NCEP
3.49
14.5
Winter
CTL
A2
4.06
5.66
15.8
14.8
B2
5.70
15.5
NCEP
3.81
13.70
Summer
CTL
A2
3.99
7.12
14.3
9.44
B2
7.40
10.1
Table 4.33: Frequency of wet CPs in spring and autumn [%].
CP08
CP02
NCEP
5.77
13.90
Spring
CTL
A2
4.31
5.47
15.0
17.2
B2
6.16
17.7
NCEP
4.30
16.20
Autumn
CTL
A2
3.80
6.06
16.30
13.7
B2
6.31
13.9
Table 4.34: Mean persistence of wet CPs in winter and summer [day].
CP08
CP02
NCEP
1.09
1.72
Winter
CTL
A2
1.35
1.31
2.18
2.02
B2
1.14
1.95
NCEP
1.30
2.05
Summer
CTL
A2
1.18
1.42
1.88
1.74
B2
1.46
1.69
Table 4.35: Mean persistence of wet CPs in spring and autumn [day].
CP08
CP02
NCEP
1.24
2.02
Spring
CTL
A2
1.12
1.27
1.86
2.09
B2
1.23
2.16
NCEP
1.22
2.34
Autumn
CTL
A2
1.33
1.23
1.95
1.94
B2
1.20
1.88
Table 4.36: Maximum persistence of wet CP in winter and summer [day].
CP08
CP02
NCEP
2
7
Winter
CTL
A2
8
5
10
7
B2
3
10
NCEP
3
6
Summer
CTL
A2
4
6
9
10
B2
6
8
Table 4.37: Maximum persistence of wet CP in spring and autumn [day].
CP08
CP02
NCEP
4
7
Spring
CTL
A2
4
4
8
11
B2
4
13
86
NCEP
3
12
Autumn
CTL
A2
4
4
7
9
B2
3
7
investigation. The modeled moisture flux from the control run of the GCM is slightly underestimated compared with that from assimilation model of NCEP. Therefore, it can be expected
that the generated scenarios may carry the model’s uncertainty and cause an underestimation
of the future moisture flux that may lead to the estimation of fewer future precipitations.
Of all the seasons, spring and summer are of most interest. In spring, both of the frequencies
of wet and dry CPs derived from scenarios are higher than those derived from a control run,
the same trend as that of the mean and maximum persistence. In summer, the wet CP is
inclined to occur more frequently together with a relatively longer persistence and the dry CP
with less frequency and shorter persistence. This indicates that there may be a wetter climate
condition in the summer in the future.
Zoomed in on the individual stations, the impacts on the local precipitation are presented
in the Figure 4.33 to 4.37
4.5
Observed
Exponential + MF
A2
B2
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
Figure 4.33: Precipitation between observed and simulated of current and future climate based on
ECHAM4 scenarios A2 and B2 [Station: Olygaing].
Conditioned to A2 and B2 ensembles generated by ECHAM4, it is found that it is likely to
have less precipitation in spring and summer than in the other seasons. That is, the available
water resources will be reduced as a result of a lower input. In contrast, due to an increase of
temperature in the future, there may be more water created from snow-melt available at the
beginning of the year. Unfortunately, the summer will be even warmer than it presently is,
and a little bit more rainfall will be expected.
87
3.0
Observed
Exponential + MF
2.5
A2
B2
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ECHAM4 scenarios A2 and B2 [Station: Tashkent].
5.0
Observation
4.5
Exponential + MF
A2
4.0
B2
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ECHAM4 scenarios A2 and B2 [Station: Dukant].
88
5.0
Observed
Exponential + MF
A2
B2
4.5
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ECHAM4 scenarios A2 and B2 [Station: Pskem].
5.0
Observed
Exponential + MF
A2
B2
4.5
4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
1
2
3
4
5
6
7
8
9
10
11
12
Month
ECHAM4 scenarios A2 and B2 [Station: Charvak].
89
5 Development of a multiple-site weather
generator
In the region of high latitude zones such as 30 ◦ N - 60 ◦ N in the northern hemisphere, the impact
of the Coriolis force is so strong that surface air does not move directly from the equator to
the poles, but deflects to the right in the northern hemisphere and to the left in the southern
hemisphere.
The higher the latitude, the stronger the Coriolis force. The air is swirled until it forms
distinct high and low pressure zones. This phenomenon provides the possibility to apply a
circulation pattern-based downscaling procedure as described in Chapter 3. However, in such
regions near to the equator, like the Ouémé basin in western Africa, the Coriolis force is close
to zero. The distinguished high and low pressure system does not exist any more.
A new model must be therefore developed to reproduce the daily precipitation for the study
area.
5.1 Introduction
The new model is developed based on the same methodology as that for the normal downscaling
method used in combinations with CPs. Here, no CPs is used. The parameters of the model are
estimated using MLE described in Chapter 3.3.4. In climate impact study, model’s parameters
are varied according to the relative changes between GCM’s control runs and scenario runs.
5.2 Application of a weather generator in Ouémé Basin in western
Africa
5.2.1 Study area
Description of river basin
The Ouémé River is the largest river within the Republic of Benin in western Africa, it provides
a water source for agriculture and domestic purposes. The upper Ouémé covers an area near
90
to the southern Sahel and the lower Ouémé covers an area near to the Gulf of Guinea. The
entire basin is approximately 45, 000 km2 and extends out over almost the entire country.
The local climate is characterized by its distinct dry and rainy seasons. In general, the rainy
season starts in April and finishes in the end of October, and it contributes the majority of
the annual rainfall amount. According to the particular geophysical location of an individual
precipitation station, the temporal distribution of rainfall over a year can be completely different. In Figure 5.1, three representative stations located in the Upper, Middle and Lower
catchments are chosen to reflect the local annual rainfall variabilities.
Figure 5.1: Representative temporal distribution of annual precipitation in the Ouémé basin.
In the Upper Ouémé, near to the southern Sahel, the local rainfall presents an unimodal
property such as in Parakou. The monthly precipitation is quite limited at the beginning of
the year. It starts to increase and reaches its annual peak in August. The rainfall events lasts
for 6 to 7 months, in the rest of the year it is almost completely dry. In the Middle Ouémé,
the monthly precipitation during the rainy season is distributed quite evenly and there is no
particular month that was extreme large rainfalls. In the Lower Ouémé, two peaks can be
clearly observed. One normally occurs in the middle of the big rainy season and the other is
in the middle of the small rainy season.
The average temperature in the Ouémé River Basin is between 24 ◦ C and 31 ◦ C throughout
the whole year. The difference between the annual maximum and the minimum daily maximum
temperature is quite small, approximately 5 ◦ C. The highest temperature occurs in the dry
season and the temperature in the rainy season is relatively low.
91
Data availability
Observation records were provided by Agence pour la Sécurité de la Navigation Aérienne en
Afrique et á Madagascar (ASCENA). There are 133 rainfall stations and 122 temperature
stations distributed over the whole river basin. However, only a few of these stations contain
properly-measured records over the past 20 years or longer. Due to data limitation, seven rainfall stations covering a time period from the year 1980 to 2003 were applied to the downscaling
model. These seven stations are Kandi, Natitingou and Parakou in the Upper Ouémé; Save in
the Middle Ouémé; and Ketou, Bouicon and Lonkly in the Lower Ouémé near to the Golf of
Guinee.
The rainfall records are split into two parts. The data collected from the year 1980 to
the year 1995 is used for model’s training and data collected from 1996 to 2003 is used for
validation.
5.2.2 Multi-site weather generator
General introduction
Weather generators have been developed to meet the requirement for water engineering management, ecosystem, climate change impact studies and others. The models are mainly used to
fill in missing values or produce infinitely-long synthetic weather series by maintaining the key
properties of the observed meteorological variables. These characteristics include probability,
daily mean and variance of precipitation events.
As mentioned in the previous chapters, precipitation is characterized by its unique attributes
of being a continuous and discrete variable. The rainy day and non-rainy day always occur
consecutively. Accordingly, most weather generators need to handle both precipitation occurrence and precipitation intensity separately and in an appropriate way. Whether the model
is able to represent the persistence of a rainy or dry day, day-to-day dependence and rainfall
amount is a key aspect for the model’s evaluation.
In the aspect of precipitation occurrence studies, the most well-known approach is the application of a first-order Markov chain model. This model assumes the probability of a day being
wet is strongly dependent on the weather situation of the day before. The model’s assumption
were studied by Gabriel and Neumann in 1962. The long-term relative frequency of precipitation days is calculated with Equation 2.5 and the 1-day lag autocorrelation is calculated with
Equation 2.6. There is also another approach to simulate the occurrence of precipitation using
an empirical distribution of the length of series of wet or dry days. LAR-WG is a weather
generator developed based on this underlying concept. Once the weather state of the studied
day is defined, the rainfall intensity can be generated using the aforementioned distributions.
92
The flowchart of these two weather generators are presented in Figure 5.2.
(a)
(Begin Next Day)
Generate
uniform
random
number, u
f(u)
Generate today‘s
Non-ppt.
variables
u
Generate
ppt. = 0
Pc = P01
Dry-day non-ppt.
parameters:
µk, 0; σk, 0
Generate a nonZero ppt.
amount
Pc = P11
Wet-day non-ppt.
parameters:
µk , 1; σk, 1
No
u ≤ Pc ?
Yes
f(x)
x
Precipitation Submodel
(b)
Non-precipitation Submodel
(Begin Next Day)
L=0?
Yes
p(L)
No
L = L-1
L
No
Is this a
wet spell?
Generate a new
spell length, L, of
opposite type
Generate today‘s
Non-ppt.
variables
Dry-day non-ppt.
parameters:
µk, 0; σk, 0
Generate
ppt. = 0
Yes
f(x)
Generate a nonZero ppt.
amount
Wet-day non-ppt.
parameters:
µk , 1; σk, 1
x
Precipitation Submodel
Non-precipitation Submodel
Figure 5.2: Flowcharts for daily weather generation using the WGEN framework and (a) Markov chain
and (b) spell-length models for the precipitation component (Wilks and Wilby, 1999).
Normal distribution based weather generator
In this section, a weather generator that is capable of simultaneously handling the precipitation
occurrence and precipitation intensity is introduced. This model is set up with a normal
distribution to simultaneously reproduce rainfall occurrence and amounts.
As mentioned in Chapter 3.3.2, the Box-cox transformation is always required to correct the
skewness of strongly skewed precipitation time series into a symmetrical normal distribution.
For each station, two parameters of normal distribution, µ and σ are calibrated by time series of
observation records. Their temporal variations are represented using the Fourier series shown
in Equation 5.1 and 5.2. The definitions of the variables are the same as those in Equation
93
5.1.
K
a0 (i, u) X
µ(t , u) =
+
2
∗
(5.1)
k=1
K
a0 (i, u) X
+
σ(t , u) =
2
∗
(5.2)
k=1
Given the specific values of specific µ and σ, the weather state of a specific day being wet
and rainfall amounts can be determined. The spatial covariance is calculated by the method
described in Chapter 3.3.3.
Downscaling for climate scenarios
To get a projection of climate scenarios and their impacts on the local events, the weather
generator has been applied as one important model.
The relationship of daily precipitation-related parameters such as daily precipitation amount
and its rainfall probability between the GCM control runs and scenarios reflects how the future
climate will vary from the present one. Such a relationship is then applied to the observations
to project the image of precipitation in the future.
5.2.3 Evaluation of the model’s performance
The performance of the annual cycle is one of the indicators to evaluate a model’s performance.
As seen in Table 5.1, the annual precipitation in the Ouémé river basin is averaged around
1000 mm per year, while the variability from year to year increases from the northern to the
southern stations. Our model is able to well simulate annual total precipitation for all of
the 7 stations, but is weaker at representing inter-annual variability. The monthly totals at
each station are well represented by the annual cycle, but there is an underestimation of peak
precipitation in the rainy seasons. This weakness is particularly dominant in the southern part
of the river basin.
In order to compare the model’s performance with observations, diagnostics have been applied. These diagnostic indices include average precipitation [Pav], 90th percentile of rainy
day’s amounts [P90], consecutive wet days [CWD], mean wet-day persistence [Pww], mean
dry-day persistence [Pdd], mean wet spell [Lw], mean dry spell [Ld] and maximum dry spell
[Ldm]. These indices are recommended by the EU-funded STARDEX project. 3 stations
located in the Upper Ouémé, Middle Ouémé and Lower Ouémé respectively are selected to
compare different rainfall behaviors.
Table 5.2 shows that the model’s output generally underestimates mean precipitation for
all of the 3 stations, while the simulated 90th percentile of precipitation is not far away from
94
Table 5.1: Average and variance of annual precipitation for the years from 1980 to 1995.
Station
Annual precipitation
Standard deviation
Observed
Simulated
Observed
Simulated
Kandi
900.8
896.3
135.9
195.4
Natitingou
1134.8
1086.7
152.2
93.4
Parakou
1148.8
1093.8
264.3
112.6
Save
1015.4
931.0
193.7
131.8
Ketou
1031.5
1055.8
201.1
126.9
Bohicon
1039.0
1021.3
211.7
169.5
Lonkly
1046.8
1020.8
307.9
156.2
Table 5.2: Extreme indices derived from different model’s settings [Wet seasons].
Indices
Pav
P90
CWD
Pww
Pdd
Lw
Ld
Ldm
Unit
mm
mm
day
day
day
day
Parakou
(upper Ouémé)
Observed Simulated
4.91
4.86
34.1
36.9
5.3
5.1
0.38
0.36
0.69
0.72
1.63
1.59
3.05
3.51
14.7
14.67
Save
(middle Ouémé)
Observed Simulated
4.41
3.87
32.4
31.2
4.95
4.6
0.36
0.34
0.72
0.74
1.56
1.53
3.50
3.83
14.55
15.08
95
Boihcon
(Lower Ouémé)
Observed Simulated
4.26
4.04
35.0
34.0
4.75
4.42
0.32
0.32
0.72
0.74
1.50
1.48
3.70
3.82
17.5
14.38
that derived from observations. The conditional probability of Pww and Pdd give comparable
results.
To obtain the image of climate change on the future climate conditions in the Ouémé basin, two
different scenarios, A2 and B2 generated from the ECHAM4 model, are selected. There are 3
grid-cells covering the regions inside Benin. Grid-cell 1 covers the southern part of Niger and a
small part of northern Benin; grid-cell 2 covers most of the region in northern Benin and gridcell 3 covers the region in southern Benin. The precipitation-related and temperature-related
parameters of these 3 grid-boxes, derived from the control run and corresponding scenarios,
are calculated and compared to determine the trend of climate changes in the coming 30
years. These precipitation-related parameters include the amount of monthly precipitation,
the standard deviation of the monthly precipitation and the probability of precipitation for
each month. The temperature-related parameters consist of monthly maximum temperatures
and monthly minimum temperatures.
Since the study area is in the middle and lower parts of the Ouémé basin, the behaviors of
grid-cell 2 and grid-cell 3 are of interest. In the following sections, variables derived from these
2 grid-cells are used. Their corresponding results are indicated as the combination of scenario
information and grid information. For instance, scenario A2-2 indicates the result derived from
grid-cell 2 conditioned to the A2 scenario. The real values of these parameters are presented
in Tables 5.3 to 5.8. The ratios between meteorological parameters derived from the control
run and the scenarios are calculated and further applied for impact studies.
Table 5.3: Daily precipitation (mm) for each month derived from the control run (1960-1990).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
CTL-2
0.00
0.17
1.09
3.46
6.71
8.00
7.98
8.14
6.83
3.92
0.51
0.02
CTL-3
0.15
1.65
3.83
5.6
9.13
9.64
7.72
5.96
6.53
5.44
1.53
0.34
As an integral response to the key properties of precipitation, the annual cycles of several
stations conditioned to A2 and B2 scenarios are generated. For those stations located in the
northern part, both A2 and B2 scenarios show the increase in the amount of precipitation
in rainy seasons, especially in August. Scenario A2 even suggests there will be more rainfall
than scenario B2. For those stations located in the southern part of the river basin, scenarios
show the reduction of precipitation in rainy seasons. No significant difference can be identified
between the A2 and B2 scenarios (Figure 5.5 to 5.9).
96
Table 5.4: Daily precipitation (mm) for each month derived from A2 scenarios generated by ECHAM4
(2000-2030).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
A2-2
0.00
0.12
1.29
3.54
7.45
8.26
8.59
8.69
8.03
3.98
0.49
0.01
A2-3
0.1
1.55
3.77
5.7
9.85
9.11
7.51
5.48
6.50
5.76
1.60
0.09
Table 5.5: Daily precipitation (mm) for each month derived from B2 scenarios generated by ECHAM4
(2000-2030).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
B2-2
0.00
0.06
0.85
3.83
6.83
8.18
8.39
8.31
7.98
3.95
0.39
0.01
B2-3
0.20
1.56
3.49
5.88
9.61
9.17
7.19
5.75
6.50
6.09
1.24
0.15
Table 5.6: Standard deviation of daily precipitation for each month derived from the control run
generated by ECHAM4 (1960-1990).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
CTL-2
0.00
0.44
0.99
1.57
2.08
1.66
1.31
1.36
1.41
1.33
0.85
0.06
CTL-3
0.38
1.16
1.10
1.96
2.04
2.25
1.64
1.53
1.57
1.33
1.10
0.53
Table 5.7: Standard deviation of daily precipitation for each month derived from A2 scenarios generated by ECHAM4 (2000-2030).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
A2-2
0.02
0.44
1.37
1.10
1.87
2.65
1.50
1.26
1.36
1.60
0.63
0.04
A2-3
0.20
1.08
1.20
1.92
2.13
2.82
1.55
1.63
1.67
1.66
0.95
0.17
Table 5.8: Standard deviation of daily precipitation for each month derived from B2 scenarios generated by ECHAM4 (2000-2030).
Jan
Feb
Mar
Apr
May
June
July
Aug
Sept
Oct
Nov
Dec
B2-2
0.02
0.21
0.94
1.27
2.23
1.86
1.33
1.23
1.31
0.26
0.66
0.06
B2-3
0.31
1.53
1.21
1.70
2.37
2.18
2.10
1.61
1.42
1.55
0.90
0.24
97
1.60
Ratio between scenarios to control run [-]
1.40
1.20
1.00
1
2
3
4
5
6
7
8
9
10
11
12
0.80
0.60
0.40
0.20
SA2/CTL-2
SB2/CTL-2
0.00
Month
Ratio between scenarios and control run [-]
1.60
1.40
1.20
1.00
1
2
3
4
5
6
7
8
9
10
11
12
0.80
0.60
0.40
0.20
SA2/CTL-3
SB2/CTL-3
0.00
Month
Figure 5.3: The ratios between monthly precipitations derived from scenarios and those from the
control run.
98
Ratio between scenarios and control run [-]
1.80
1.60
1.40
1.20
1.00
1
2
3
4
5
6
7
8
9
10
11
12
0.80
0.60
0.40
0.20
SA2/CTL-2
SB2/CTL-2
0.00
Month
Ratios between scenarios and control run [-]
1.60
1.40
1.20
1.00
1
2
3
4
5
6
7
8
9
10
11
12
0.80
0.60
0.40
0.20
SA2/CTL-3
SB2/CTL-3
0.00
Month
Figure 5.4: The ratios between the standard deviation of monthly precipitations derived from scenarios
and those from the control run.
99
Figure 5.5: The comparison between monthly precipitation derived from observation, simulation and
scenarios at station Kandi.
scenarios at station Natitingou.
100
scenarios at station Parakou.
scenarios at station Save.
101
scenarios at station Lonkly.
102
6 Development of a multivariate downscaling
model using copulas
In most applied statistical fields, a multivariate analysis (MA) is always required and is used as
a valuable tool to achieve several goals: data reduction, dependence analysis, sorting, grouping
and prediction, etc. The methods pertaining to multivariate analysis have been widely applied
in many aspects of scientific and social study fields such as in biology, medicine and health,
business and economics, psychology and so on. In the field of natural science like meteorology
and hydrology, multivariate analysis is also of great importance.
In this Chapter, Copula is to be introduced as a tool to describe the dependence between
daily precipitation and moisture flux. The aim of model development was to represent different
dependence structures depending on different magnitude of precipitation and moisture flux.
Thus, the developed model was expected to improve the reproduction of extreme rainfall events.
6.1 Introduction
Atmospheric variables are normally vector observations. They can be simultaneously measured observations of different variables at one location, or an atmospheric field characterized
by measurements at different grid points. Apart from that, the collected data may contain
redundant information that is normally required to be removed to simplify the structure of
the studied phenomenon. In hydrology, interdependence in general exists amongst several
hydrology-related variables. For example, the routing of river flow is determined by its upstream tributaries; the local rainfall events are the results of large scale atmospheric motions.
Both examples are of typically multivariate analysis studies.
The aim of multivariate analysis is to represent the dependence identified from the observations. Therefore, the appropriate joint distribution and marginal distributions of the studied
variables must be carefully selected in the conventional multivariate analysis process. The
most commonly used is probably the multivariate normal distribution whose individual univariate is normally distributed. The joint distribution has 2n +
n(n−1)
2
parameters: the mean
and standard deviation for each variable (2n) and correlation between each pair of variables
n(n−1)
.
2
The mean and standard deviation are calculated directly from a batch of samples and
103
correlations are estimated using Pearson correlations. The normal joint distribution is easy
to be implemented, however, it has the obvious limitations: (1) not all the variables can be
characterized by the normal distribution and therefore the transformation is always required;
(2) transformed variable normally lose tail information contained in the extreme events.
Apart from the multivariate normal distribution, the multivariate gamma type distribution,
multivariate exponential distribution, and multivariate poisson distribution are also quite often
used. They also contain the same limitation that each variate must follow the same marginal
distribution in order to implement the joint distribution.
Copula, which is free of aforementioned restrictions, is a modern tool to describe the dependence amongst the variables. The concept of copula is not new, its first implementation
can be traced back to 1959. Copula has been widely applied in the field of economics due to
its capability of describing the dependence in the risks. Recently, it is also used in the field
of hydrology. Favre (Favre et al., 2004) applied it to solve two aspects of hydrologic problem.
One is used to estimate the flooding risk induced by two upstream flow regimes; the other is
carried out for flooding frequency analysis in terms of the flow and volume. In a recent work
(Bárdossy, 2006), the capability of copulas for geostatistical interpolation was described. Here,
the application of copula to generate discrete-continuous rainfall data and its performance in
representing the extreme events is of great concern.
6.2 Basics of copula
Copula is a relatively new word, which means “a link, a bond and a tie”. From the statistical
point of view, copula is a function that couples one-dimensional uniform distribution functions
to a multivariate joint distribution. In brief, it is a collection of multivariate distributions
whose marginal distribution functions are uniformed on the space (0,1) as shown in Equation
6.1.
C : [0, 1]n −→ [0, 1]
(6.1)
Let Fj (j) be marginal distributions of j uni-variate; F (F1 , F2 , . . . , Fj ) be a multivariate
distribution for j uni-variate. When all the uni-variate are uniformed on the space (0, 1), the
copula-based joint distribution is expressed as in Equation 6.2, where C is a copula:
F (x1 , x2 , . . . , xn ) = C(F1 (x1 ), F2 (x2 ), . . . , Fn (xn ))
(6.2)
Copula contains several properties that are derived from its (0,1) working spaces. Here, bivariate copula, the simplest form of copulas, is used as an example to present the copula properties
in Equations 6.3 to 6.6, u and v are two random variables.
0 ≤ C (u, v) ≤ 1
(6.3)
104
C (u, 0) = 0 = C (0, v)
(6.4)
C (u, 1) = u and C (1, v) = v
(6.5)
For every u1 , u2 , v1 , v2 , u1 ≤ u2 and v1 ≤ v2 ,
C (u2 , v2 ) − C (u1 , v2 ) − C (u2 , v1 ) + C (u1 , v1 ) ≥ 0
(6.6)
When n variables are considered, the probability function of copula can be extended to n
P
k
dimensions. See Equation 6.7, where i = n−1
k=0 jk 2 .
n −1
2X
Pn
(−1)
i=1 ji
C(u1 + j1 ∆1 , . . . , un + jn ∆n ≥ 0
(6.7)
j=0
As with classic distributions, the copula density can be derived from its copula probability
distribution when the involved marginal distributions are continuous. In Equations 6.8 and
6.9, the copula density and its corresponding conditional copula are presented.
∂ n C(u1 , . . . , un )
c(u1 , . . . , un ) =
∂u1 . . . ∂un
C(u1 |U2 = u2 , . . . , Un = un ) =
∂ n−1 C(u1 , . . . , un )
∂u2 . . . un
(6.8)
(6.9)
Copulas contain the following advantages over the other MA approaches: 1) the marginal
distributions are uniformed in the range (0,1). It makes the correspondent multivariate distribution invariant to the transformation of any marginal distribution. 2) the copula is capable
of describing dependence structures amongst different quantile of the studied variables.
Several parametric families of copulas have already been developed. They are one-parameter
families such as Plackett copula, Frank copula, Gumbel copula, etc and two-parameter families.
Two-parameter copulas are normally used to capture more than one type of the dependence.
With different combination of the two parameters, the resultant copula is able to explain the
different type of the dependence structures. The detailed explanation of copula properties can
be found in Nelsen or Joe’s works (Nelsen, 1999; Joe, 1997).
In the following sections, two types of copulas are applied to describe the continuous and
discrete properties of rainfall time series. The Neckar River Basin is used to demonstrate the
model’s performances.
6.3 Application of copula
6.3.1 Empirical copula
In this thesis work, the dependence of daily precipitation on moisture flux (MF), given a
particular circulation pattern, is studied. The circulation patterns are prepared using the
method described in Chapter 3.1.
105
Empirical copulas are obtained from the observations. There are two possibilities to explore
the dependence between rainfall and moisture flux (MF).
1. To investigate the dependence of precipitation occurrence and MF, and the dependence
between precipitation amounts and MF when precipitation occurs.
2. To investigate the relationship between precipitation and MF simultaneously.
Here, the second possibility is considered.
Let Z1 (1), . . . , Z1 (T ) be the precipitation on days from 1 to T, and Z2 (1), . . . , Z2 (T ) be the
corresponding moisture flux. The ranks of precipitation are R1 (1), . . . , R1 (T ), and the ranks
of moisture flux are R2 (1), . . . , R2 (T ). The empirical copulas is then described with Equation
6.10 (Deheuvels, 1979).
T
1 X R1 (t)
R2 (t)
C (u, v) =
1(
≤ u,
≤ v)
N
N
N
∗
(6.10)
t=1
The density of this copula is calculated using local smoothing, and Figure 6.1 shows the
copula density calculated between the precipitation and MF. Note that the intermittent property of rainfall does not allow a unique characterization of the copula for the dry days. For
dry days, only the conditional marginal of moisture flux can be identified. As seen from the
Figure, a very strong asymmetrical distribution with respect to the minor diagonal can be
noticed. The dependence in the upper right corner differs quite a lot from that in the rest
of the spaces, particularly, the region in the lower left corner. This implies that the moisture
flux and precipitation are strongly dependent on each other, when both of them are in the
range of the higher rank. However, when their ranks are lower, no dominant dependence can
be determined.
The impact of circulation patterns on the dependence structures between precipitation and
moisture flux were also studied. The results are prepared as density maps and can be visualized
in Figures 6.2 and 6.3. In the figures, the x-axis stands for the percentile of the precipitation
amount conditioned on individual CP, while the y-axis stands for the percentile of the moisture
flux under impact of the same CP. The magnitude of density is differentiated in colors. The
darker the red, the higher the density is. Each density map is separated into two part and each
of them shows the interdependence structure between these two variables under the different
weather state. The shaded part of the figure shows the dependence under the dry conditions,
and the other part of the figure shows the dependence under rainy conditions. The intersect
stands for the rainfall probability under the impact of a specific CP.
As seen in the figures, several properties can be identified:
- dependences between precipitation amounts and moisture flux are differentiated from
one CP to the others.
106
1
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
Percentile of precipitation
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Percentile of moisture flux
Figure 6.1: Relationship between percentile of daily precipitation and the moisture flux
107
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
Dry
0
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0.2
0.3
0.4
0.1
Dry
0
0.5
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0.2
0.3
0.4
0.1
Dry
0
0.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
Figure 6.2: Empirical interdependence between the uniformed moisture flux and precipitation [CP01CP06]
108
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
Dry
0
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0
0.1
0.2
0.3
0.4
0
0.1
0.2
0.3
0.4
0.1
Dry
0
0.5
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
Dry
0
0.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
Figure 6.3: Empirical dependence between the uniformed moisture flux and precipitation [CP07CP12].
109
- These dependences are non-Gaussian distributed, different for the upper tail and lower
tail.
For the dry CPs such as CP05, the strongest dependence exists in the range of higher rank
of precipitation and moisture flux, which shows the similarity to the dependence when no CP
is considered. For the wet CPs, for example, CP11, two regions with stronger dependences can
be identified. These two regions are located at the both end of tails. One occurs in the upper
tails when the moisture flux is higher than 90%, the other in the lower tails when the moisture
flux is below 5%. This proves the significance of the CPs, which is important to determine the
dependence between precipitation and the moisture flux.
6.3.2 Theoretical copula
To present the aforementioned relationship between precipitation and the moisture flux, an
appropriate copula needs to be selected. Two copulas were applied. One is Gumbel copula
and the other is χ2 copula derived from normal copula.
Gumbel copula
Gumbel copula is one type of one-parameter Archimedean copulas. It contains one parameter,
δ, larger or equal to 1. The distribution function of a bivariate Gumbel copula is expressed as
in Equation 6.11:
1/δ δ
δ
C(u, v; δ) = exp − u
e + ve
(6.11)
The density is calculated with Equation 6.12:
c(u, v; δ) = C(u, v; δ)(uv)−1
h
i
(ũṽ)δ−1
δ
δ 1/δ
(ũ
+
ṽ
)
+
δ
−
1
(ũδ + ṽ δ )2−1/δ
(6.12)
Where, ũ and ṽ are the logarithms of uniformed univariate u and v respectively. According to
the value of the parameter δ, the Gumbel copula is able to show the upper tail dependence at
different magnitudes. The larger the δ is, the stronger the dependence is in the upper tail.
One example is given in Figure 6.4. As shown in the figure, the dependence structure
described by the Gumble copula can be seen with two strong dependence regions. The major
one appears in the upper right corners and the minor one in the lower left corners. Furthermore,
as δ increases, the dependence become less along the diagonal and those in the upper and
lower tails are further concentrated. The generated density maps based on the Gumbel copula
show the similarity to those empirical density maps derived from the observations as shown in
Chapter 6.3.1, especially for the wet CPs. Therefore, the Gumbel copula is considered as one
of the candidates to present the joint distribution of precipitation and the moisture flux.
110
Figure 6.4: Contour maps of Gumbel copula with different values of β (left: β=2; right: β=6)
χ2 copula
χ2 copula is a non-Gaussian distribution copula, which is able to describe the dependence
amid uni-variate that follow the χ2 distribution. As a widely applied theoretical probability
distribution, χ2 distribution is used to describe the random variables that are independent and
normally distributed with expectation of 0 and standard deviation of 1. The summed squared
of such random variables follow the χ2 distribution. Its expression is shown as in Equation
6.13:
Xj = Yj2 , j = 1, 2, 3 ...n
(6.13)
The details of constructing a χ2 copula can be found in Bárdossy’s work in 2006. Here,
only a brief is given. Let Y be an n-dimensional normally distributed random variables with
mT = (m1 , m2 , ,̇m) and correlation matrix Γ. Its marginal distribution and density function
are derived from the normal copula and are obtained using Equations 6.14 and 6.15. φ is the
distribution function of normal distribution. Its n-dimensional multivariate distribution can
be further extended and as well as the density function.
G(t) = P (X 2 ≤ t)
√
√
= P (− t ≤ X ≤ t)
√
√
= −φ( t) − φ(− t)
√
√ −2 xyr+x+y
2r xy
exp
)
1
+
exp
2
2(r −1)
r 2 −1
g2 (x, y) = K2
√
4π xy
(6.14)
(6.15)
χ2 copula contain two parameters, mean m and variance ρ. According to the different values
of m and ρ, the copula can present a variety of extreme value dependence.
111
m = 0 ρ = 0.75
Figure 6.5: Dependence structure described by the χ2 copula
112
m=1
Figure 6.5 shows a typical dependence structure described by the χ2 copula. m is a parameter
that controls the dependence structures. If m = 0, the generated copula shows a strong
asymmetrical structure and the upper quantile of the distribution is heavily dependent. As
the value of m increases, the joint distribution tends to be more and more symmetrical. Once
m → ∞, the copula is converged to be a normal copula. ρ is a parameter reflecting the
correlation of the underlying normal variables Y as in Equation 6.13. As expected, the higher
the value of ρ, the stronger the dependence it indicates. Compared with the Gumbel copula,
χ2 copula has more freedom to represent different dependence structures identified from the
observations. Therefore, χ2 copula is taken as another candidate into consideration.
6.3.3 Parameter estimation and rainfall generation
Parameter estimation
In the application of the Gumbel copula, there is one distribution-related parameter. The
maximum likelihood estimation (MLE) is used to get the optimal value for the parameter.
The expression for the application of MLE is presented with Equation 6.16. Φ and ϕ indicate
the cumulative distribution function (CDF) and density function (PDF) of the Gumbel copula
respectively.
L(.) =
X
Z(t,u)≤0
logφ(δ) +
X
logϕ(δ)
(6.16)
Z(t,u)0
When applying the χ2 copula, two distribution-related parameters must be determined. The
first one is m, which governs the shape of the dependence structure. With the different value of
m, the generated dependence shows different structures, either asymmetrical or symmetrical
and to which extent. Therefore, m is more important compared with another parameter
ρ. One can estimate appropriate m and ρ via the Maximum likelihood estimation (MLE). Its
expression is shown with Equation 6.17, where θ stand for the cumulative distribution function
(CDF) and ψ for the density distribution function (PDF) of χ2 copula.
L(.) =
X
Z(t,u)≤0
logθ(m, Γ) +
X
logψ(m, Γ)
(6.17)
Z(t,u)0
The skewed normal distribution and the exponential distribution are used as a marginal
distribution for the daily precipitation. The parameters of each distribution and the parameter
related to the rainfall probability are obtained using the same methods described in Chapter
3.3.4.
113
Figure 6.6: Conditional probability of precipitation with given moisture flux at different quantiles
Rainfall generation
The daily precipitation is generated with the help of the conditional probability of the copula
models. Its general form is shown as in Equations 6.18 and 6.19. u indicates the percentile
of precipitation and v indicates the percentile of the moisture flux. Using the conditional
probability, the conditional distribution with given quantile of variate, for example, moisture
flux, can be differentiated (See Figure 6.6).
C(U < u|V = v) =
c(u|v) =
∂C(u, v)
/fv (v)
∂v
(6.18)
∂ 2 C(u, v)
/fv (v) = c(u, v)/fv (v)
∂u∂v
(6.19)
The generation of daily precipitation follows four steps: 1) acquire the circulation pattern and
the moisture flux on a day t; 2) formulate the conditional probability with the copula parameter
δ, or m and ρ; 3) get the percentile of precipitation using the conditional probability; 4) get the
real value of precipitation using the marginal distribution such as a skewed normal distribution
or an exponential distribution or others.
114
6.3.4 Model performance
Generals
The daily records of precipitation in the Neckar River Basin are used for the model’s evaluation.
Records from 1960 to 1979 and from 1994 to 1999 are used for the model’s training and rest
of the records for the model’s application. Four models are implemented and corresponding
descriptions are summarized in Table 6.1. Models’ performances can be evaluated through the
graphical comparisons such as the density maps or the distribution of the generated rainfall
events, particularly in extreme events.
Table 6.1: Description of the copula-based models.
Models
Multivariate distribution
Marginal distribution
A
Gumbel copula
B
Gumbel copula
C
χ2
D
χ2 copula
copula
CP-dependent copulas
As shown in Figures 6.2 and 6.3, the dependence between daily precipitation and the moisture
flux (MF) vary according to a particular CP. The scatter plots constructed with given moisture flux and artificial time series simulated by the copulas are compared to that constructed
with observations. The comparisons are conducted from CP to CP. It is expected that the
dependence field identified from the observations can be reflected by the model’s simulation
under the impact of same moisture flux and circulation patterns.
In Figure 6.7, the copula fields based on the Gumbel copula influenced by two identified
critical CPs are presented. The results show that the Gumbel copula well represent the major dependence between precipitation and the moisture flux under the impact of completely
different CPs.
Figures 6.8 and 6.9 present the dependence influenced by a dry CP, CP05, and a wet CP,
CP11. The first one of each figure stands for the relationship between the moisture flux
and the observed precipitation, the rest of the figure stand for the relationship between the the
moisture flux and simulated precipitation using the different m values. Generally speaking, the
χ2 copula is still able to represent the dependence between these two variables identified from
the observations. When the m is smaller, near to zero, the dependence structure generated with
the simulated precipitation time series is quite comparable to that based on the observations.
115
CP11
CP05
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
Dry
0.1
0.1
0
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.1
0.2
0.3
0.4
Dry
0.3
0.3
0.2
0.2
0.1
0.1
0
0.4
0.5
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
Percentile of Moisture flux
Figure 6.7: Dependence derived from the observation (left) and simulation with model A and B (right)
116
1
1
Observation
0.9
m = 0.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
1
1
m = 0.5
0.9
m = 1.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0
1
0.1
0.2
0.3
1
1
m = 1.5
0.9
m = 2.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0
1
1
0.1
0.2
0.3
1
m = 2.5
0.9
m = 3.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
Figure 6.8: Dependence structure of precipitation and the moisture flux influenced by CP05
117
1
1
Observation
0.9
m = 0.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
0.4
0.5
0.6
0.7
0.8
0.9
1
1
m = 0.5
0.9
m = 1.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
0
0.1
0.2
0.3
1
m = 1.5
0.9
m = 2.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
0
0.1
0.2
0.3
1
m = 2.5
0.9
m = 3.0
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
Figure 6.9: Dependence structure of daily precipitation and the moisture flux driven by CP11
118
CP11
CP05
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
Dry
0.1
0.1
0
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
1
1
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
0.5
0.5
0.4
0.1
0.2
0.3
0.4
Dry
0.3
0.3
0.2
0.2
0.1
0.1
0
0.4
0.5
0.6
0.7
0.8
0.9
1
0.6
0.7
0.8
0.9
1
Dry
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
10
9.5
9
8.5
8
7.5
7
6.5
6
5.5
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
0
-0.5
Percentile of Moisture flux
Figure 6.10: Dependence derived from the observation (left) and simulation with model C and D(right)
119
Rainfall distributions
As discussed in Chapter 4.1.5, the presented model has been enhanced to reproduce the extreme
events; however, there are still fewer larger rainfall events that can not be reproduced using
the new CP- and regression-based rainfall generator. Apart from that, the copulas contain the
property of representing different dependence in one joint distribution and they are expected
to represent the extreme events better than the normal classical joint distributions. Therefore,
whether the copula-based downscaling model is able to enhance its performance in terms of the
frequency of extreme events is considered as a criterion to evaluate the model’s performances.
1000
Observation
Skewed normal m = 0.0
Exponential m = 0.0
Exponential m = 1.0
Exponential m = 2.0
Exponential m = 3.0
900
No. of precipitation events
800
700
600
500
400
300
200
100
0
0
0~5
5~10
10~15
15~20
20~25
25~30
30~35
35~40
40~45
45~50
50~55
Precipitation amount [mm]
Figure 6.11: Distribution of precipitation based on a variety of m values under the impact of CP05
at Station FELDBERG/SCHW. (WST)
In Figures 6.11 and 6.12, the importance of selecting an appropriate marginal distribution
can be noticed. The distributions of the generated precipitation can be quite different despite
the same joint distribution is used. The exponential distribution turns out to better represent
precipitation distribution in comparison to the skewed normal distribution. In addition, m
shows its significance in adjusting the distributions. Those values of m close to zero can be
considered as proper values for precipitation-moisture flux dependence.
Histograms are prepared for the observations, the simulated precipitation with the CP-based
rainfall generator, the CP- and regression-based rainfall generator, the Gumbel copula based,
and the χ2 copula based rainfall generator. Their performances are shown in Figures 6.13 to
6.14.
It is clear that the number of extreme rainfall events generated by the copula-based rainfall
120
250
Observation
Exponential m = 0.0
Exponential m = 1.0
Exponential m = 2.0
Exponential m = 3.0
200
150
100
50
0
0
0~5
5~10
10~15
15~20
20~25
25~30
30~35
35~40
40~45
45~50
50~55
55~60
>60
Precipitation amount [mm]
Figure 6.12: Distribution of precipitation based on a variety of value m under impact of CP11 at
Station FELDBERG/SCHW. (WST)
5000
100
Observation
Observation
Circulation pattern based
CP+ Regression
CP+ Regression
Gumbel_normal
Gumbel_normal
Gumbel_exp
Chi-squared_normal m=1.5
Gumbel_exp
Chi-squared_exp
m=1.0
Chi-squared_normal
m=1.5
Chi-squared_exp m=1.0
90
4500
80
4000
3500
3000
2500
70
60
50
40
30
20
2000
10
0
1500
30~35
35~40
40~45
45~50
50~55
55~60
>60
Precipitation amounts
1000
500
0
0
0~5
5~10 10~15 15~20 20~25 25~30 30~35 35~40 40~45 45~50 50~55 55~60 >60
Figure 6.13: Distribution of rainfall amounts [mm] amongst different models at Station FELDBERG/SCHW. (WST) [Calibration]
121
80
3500
Observation
CP+ Regression
Gumbel_normal
Gumbel_exp
Chi-squared_normal m=1.5
Chi-squared_exp m=1.0
70
60
3000
2500
2000
50
40
30
20
1500
10
0
1000
30~35
35~40
40~45
45~50
50~55
55~60
>60
500
0
0
0~5
5~10
10~15 15~20 20~25 25~30 30~35 35~40 40~45 45~50 50~55 55~60
>60
Precipitation amount
Figure 6.14: Distribution of rainfall amounts [mm] amongst different models at Station FELDBERG/SCHW. (WST) [Validation]
generators has been improved compared to those regression-based models.
Up to now, a new copula-based downscaling model is developed. It has been successfully
applied to the Neckar River Basin. Its performance was mainly evaluated through the representation of the dependence between precipitation and the moisture flux, and the distribution
of rainfall amount at local station. Its reproduction of extreme events is of great concern. Copulas have been proved to be an efficient tool to study the dependence between precipitation
and moisture flux. Till present stage, two copulas, Gumbel copula and χ2 copula, have been
investigated. Both copulas are asymmetrical to the minor diagonal, but symmetrical to major
diagonal copulas. However, in the reality, the dependence between precipitation and moisture
flux shows asymmetrical property to the major diagonal as well.
The application of copulas to rainfall downscaling can be further explored.
122
7.1 Conclusion
7.1.1 CP- and regression-based downscaling model
The thesis work started from the exploration of potential predictors to develop a more robust
and reliable statistical downscaling. It aims to represent the synoptic climate properties and
predict the plausible scenarios induced by climate change. The main focus is on the daily precipitation, an important input to most of the water-related models, which contains continuous
and discrete properties. It was expected that the developed model should be able to describe
temporal and spatial behavior of local precipitation in general, and reproduce extreme climate
conditions as well.
The model was developed and run using observations in Germany, and later the methodology
was transferred to the contrasting climate zones and applied to two river basins in different
regions, Central Asia and West Africa. According to the synoptic climate situations in these
regions, the developed model was adjusted to generate the reasonable daily time series of
precipitation. At the end of the thesis, a new CP-based downscaling model, set up based on
the concept of copulas, was explored and applied to the Neckar River Basin in Germany.
As a prior to CP-based downscaling process, the classification scheme and consistence of the
stochastic classification process is so dominant that an appropriate objective function needs
to be selected to well present the variability of downscaled object (Chapter 3.1). It can be
foreseen that any synoptic climatic patterns are obtained in case the sensitive predictor and
proper objective function are defined. To classify the precipitation-related CPs, the observed
daily precipitation and/or resultant discharge are the suitable predictors for the optimization
procedure. In Chapter 4.1.2, the classification scheme is proved to be sensitive to the defined
objective function rather than the sets of random numbers. It ensures the stability of fuzzy-rule
based classification.
Circulation patterns are useful to capture the large-scale influence forcing in the study
area. However, they are unable to capture the continuity of the natural system, and as a
result, the generated time series of precipitation is performed poorly in representing the interannual variability. To improve these shortcomings, a continuous predictor, the moisture flux, is
123
introduced and used to enhance the downscaling model. The new model is named the CP- and
regression-based downscaling model. In Chapter 3.3, the impact of the moisture flux on the
local rainfall probability and rainfall amounts were investigated. The results highlight that:
- Circulation patterns are able to capture the representative synoptic climate.
- Moisture flux plays an important role in local rainfall events, it is strongly influenced by
the relation to the local geography and orography.
- For the regions located at high latitudes in the northern hemisphere, the westerly moisture flux is quite dominant compared to other influencing forces.
- Rainfall amount as well as rainfall probability are impacted by the classified circulation
patterns and the moisture flux.
- Logistic regression is useful to describe the precipitation occurrence. It is able to fit regression parameters to non-linear equations for the rainfall probability using the moisture
flux as a predictor.
The CP- and regression-based model has been successfully applied to the Neckar River Basin
in Germany, western Europe and the Chirchik River basin in Uzbekistan, central Asia (Chapter
4). Although the climate conditions and data availability of those regions are completely
different, the model, developed in this thesis, is still able to reproduce daily rainfall as well as
extreme events. The model’s performance was evaluated by a diagnostic analysis, which shows
the improvement in extreme indices for evaluating the inter-annual variability. Amongst the
various model-setups, the rainfall generators with skewed normal distributions and exponential
distributions are proved to be reliable in producing reasonable rainfall time series. Furthermore,
models are in general powerful in representing the winter rainfall events; weaker in representing
transition seasons, spring and autumn; and even weaker in representing the rainfall events in
summer.
The model has been improved in the capability of reproducing the extreme events, however,
the differences between observation and the model’s simulation still remain. The occurrence of
large rainfall events has remained underestimated. Therefore, copulas are studied instead of the
CP- and regression-based downscaling model (Chapter 6). Different from the regression-based
model, the copula-based model is able to represent the different dependence structure between
the different quantiles of the variables. With this, the selection of any appropriate marginal
distribution becomes possible. In this thesis work, the Gumbel copula and the χ2 copula
were used to present the joint distribution between daily moisture flux and daily precipitation
under the control of circulation patterns. The skewed normal distribution and the exponential
124
distribution are selected as a marginal distribution to reproduce daily precipitation time series.
The results can be summarized as follows:
- Interdependencies between precipitation and the moisture flux are differentiated in the
quantiles.
- The higher the quantile of the moisture flux, the more likely it is to have a higher quantile
of precipitation on the same day.
- The χ2 copula is able to represent the joint distribution between daily precipitation and
the moisture flux better than using the Gumbel copula.
- The exponential distribution shows better capability to reproduce the large rainfall
events.
7.1.2 Weather generator
The CP-based downscaling model is suitable for those regions located in the higher latitudes,
where the Coriolis force is stronger in forming anticyclones and cyclones. By distinguishing the
location of high and low pressure zones, the synoptic climate can be differentiated. Hence, the
same methodology does not work properly in those regions where the Coriolis force is weaker,
such as in the Ouémé River Basin in western Africa, near to the equator. To downscale daily
precipitation, a weather generator was developed (Chapter 5). The model is a stochastic
statistical downscaling model using the skewed normal distribution to generate daily rainfall
time series. The model is able to simultaneously capture the annual variability of the rainfall
at specific locations over the whole basin.
7.2 Further development
As mentioned, the model’s performance has been enhanced quite a lot with the coupling of the
moisture flux. The model’s performance varies strongly depending on the seasons. The model
generally performs better in the winter, while quite weaker in the summer. This is mainly
caused by the different mechanisms governing the synoptic climate. In winter, long lasting
rainfall is often caused by the large-scale west cyclonic circulation (Caspary, 1996), which can
be captured by the classified circulation patterns. In summer, the rainfall is normally the result
of local convective motion and therefore, the rainfall event is limited to local events, which are
not representative of the large-scale CPs.
As one of the influences of the moisture flux, wind speed is a variable that is highly dependent
on model resolution (Rockel and Woth, 2007; Beniston et al., 2007). Its attribute has been
125
explored in the EU-funded PRUDENCE project. Together with the development of regional
RCMs, the generated wind fields may contain more detailed information pertaining to the local
topography and a more distinct link between precipitation and the moisture flux can possibly
be identified. In addition, the vertical variation of the moisture flux should be explored for
the improvement of the representation of local summer rainfall events. Last but not the least,
high-resolution observations such as hourly precipitation can be used for the enhancement of
CP classification.
In Chapter 6, copulas have been proved to be an efficient tool in studying the dependence
between precipitation and the moisture flux. Until now, the Gumbel copula and the χ2 copula
have been investigated. Other copulas can be investigated as well, for instance, the Metaelliptical copulas. The Metaelliptical copulas is derived from the elliptical distribution, which
is also an extension of multivariate normal distribution. Through proper selection of the parameters, different type of copulas can be derived based on the metaelliptical copulas, e.g.,
Normal copula, Student copula, Cauchy copula and so on. It provides the extra flexibilities
to model dependence amongst variables, in particular, it is useful in tail dependence analysis.
Other marginal distributions in addition to skewed normal and exponential distribution can
be applied to well reproduce the distribution of precipitation amount.
Last but not the least, the spatial covariance should also be considered and properly studied
in order to downscale the multi-site precipitation time series simultaneously.
126
Bibliography
Abramowitz, M. & Stegun, I. (1962). Handbook of mathematical functions. Dover.
Bárdossy, A. (2006). Copula-based geostatistical models for groundwater quality parameters.
Water Resources Research, 42:W11416.
Bárdossy, A. & Fulya, F. (2005). Identification of flood producing atmospheric circulation
patterns. Journal of hydrology, 313:48–57.
Bárdossy, A. & Plate, E. (1992). Space - time model for daily rainfall using atmospheric
circulation patterns. Water Resources Research, 28:1247–1259.
Bárdossy, A., Stehlı́k, J., & Caspary, H. (2002). Automated objective classification of daily
circulation patterns for precipitation and temperature downscaling based on optimized fuzzy
rules. Climate Research, 23:11–22.
Beniston, M., Stephenson, D., & Christensen, O. (2007). Future extreme events in european
climate: an exploration of regional climate model projections. Climate Change, 81:71–95.
Carter, T., Parry, M., & Harasawa, H. (1994). The ipcc technical guidelines for assessing
climate change impacts and adaptations. In: IPCC Special Report 1994.
Caspary, H. (1996). Recent winter floods in germany caused by changes in the atmospheric
circulation across europe. Physics and Chemistry of the Earth, 20:459–462.
Conway, D., Wilby, R., & Jones, P. (1996). Precipitation and air flow indices over the british
isles. Climate Research, 7:169–183.
Cubasch, U., von Storch, H., Waszkewitz, J., & Zorita, E. (1996). Estimates of climate change
in southern europe derived from dynamical climate model output. Climate Research, 7:129–
149.
Deheuvels, P. (1979). La fonction de dépendance empirique et ses propriétés: Un test non
paramétrique d’indépendance. Bull. cl. Sci.Acad.R.Belg., 65(6):274–292.
127
Bibliography
Duband, D. (1980). Dynamic selection of analogue flow patterns to produce quantitative
precipitation forecasts. In: Symposium on Probabilistic and Statistical Methods in Weather
Forecasting.
Favre, A., Adlouni, S., Perreault, L., Thiemonge, N., & Bobee, B. (2004). Multivariate hydrology frequency analysis using copulas. Water Resources Research, 40:W01101.
Giorgi, F. & Mearns, L. (1991). Approaches to regional climate change simulation: A review.
Rev. of Geophys., 29:191–216.
Gunst, R. (1995). Estimating spatial correlations from spatial, temporal, meteorological data.
Climate, 8:2454–2470.
Hack, J. (1994). Parameterization of moist convection in the national center for atmospheric
research community climate model (ccm2). Journal of geophysical research, 99:5551–5568.
Hay, L., McCabe, G., Wolock, D., & Ayers, M. (1991). Simulation of precipitation by weather
type analysis. Water Resource Research, 27:493–501.
Hess, P. & Brezowsky, H. (1969). Katalog der groesswetterlagen europas. DWD, 15.
Hewitson, B. & Crane, R. (1996). Climate downscaling: techniques and application. Climate
Research, 7:85–95.
Heyen, H., Zorita, E., & von Storch, H. (1996). Statistical downscaling of monthly mean north
atlantic air-pressure to sea level anomalies in the baltic sea. Tellus, 48A:312–323.
Hostetler, S. (1994). Hydrologic and atmospheric models: the (continuing) problem of discordant scales. Climatic Change, 27:345–350.
IPCC (2001). Climate Change 2001. Cambridge University Press.
IPCC (2007). Climate Change: 2007. Cambridge University Press.
Joe, H. (1997). Multivariate Models and Dependence Concepts. CHAPMAN & HALL/CRC.
Johnson, S. (1967). Hierarchical clustering schemes. Psychometrika, 32:141–154.
Journel, A. (1983). Non-parametric estimation of spatial distributions. Math Geology, 15
(3):445–468.
Katz, R. (1977). Precipitation as a chain-dependent process. Journal of Applied Meteorology,
16:671–676.
128
Bibliography
Kim, J., Chang, J., Baker, N., Wilks, D., & Gates, W. (1984). The statistical problem of
climate inversion: Determination of the relationship between local and large-scale climate.
Monthly Weather Review, 112:2069–2077.
Kysel, J. & Huth, R. (2003). Recent changes in atmospheric circulation over europe detected
by objective and subjective methods. Amer. Meteor. Soc., page 31.
Lahiri, K. & Moore, G. (1991). Leading Economic Indicators: New Approaches and Forecasting
Records. Cambridge University Press. New York, NY.
Lamb, H. (1972). British isles weather types and a register of the daily sequence of circulation
patterns 1861-1971. Geophys. Memoir., 116:85.
Longley, R. (1953). The length of dry and wet periods. Quarterly Journal of the Royal
Meterological Society, 79:520–527.
Lorenz, E. (1969). The predictability of a flow which possesses many scales of motion. Tellus,
21:289–307.
MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability
Berkeley, pages 281–297.
Matalas, N. (1967). Mathematical assessment of synthetic hydrology. Water Resourc. Res,
3(4):937–945.
Nelsen, R. (1999). An introduction to copulas (Lecture notes in statistics). Springer.
Newnham, E. (1916). The persistence of wet and dry weather. Quarterly Journal of the Royal
Meteorological Society, 42:153–162.
Obled, C., Bontron, G., & Garcon, R. (2002). Quantitative precipitation forecasts: A statistical
adaption of model outputs through an analogues sorting approach. Atmos. Res, 63:303–324.
Peixoto, J. & Kettani, M. (1973). The control of the water cycle. Sci. American, 228:46–61.
Racsko, P., Szeidl, L., & Semenov, M. (1991). A serial approach to local stochastic weather
models. Ecological Modelling, 57:27–41.
Richardson, C. (1981). Stochastic simulation of daily precipitation, temperature, and solar
radiation. Water Resources Research, 17:182–190.
Risbey, J. & Stone, P. (1996). A case study of the adequacy of gcm simulations for input to
regional climate change assessments. Journal of climate, 9:1441–1466.
129
Bibliography
Rockel, B. & Woth, K. (2007). Extremes of near-surface wind speed over europe and their
future changes as estimated from an ensemble of rcm simulations. Climate Change, 81:267–
280.
Roeckner, E. (1996). The atmospheric general circulation model echam-4: Model description
and simulation of present-day climate. Max-PlanckInstitut fur Meteorologie, 218:90pp.
Rummukainen, M. (1997). Methods for statistical downscaling of gcm simulations. RMK, 80.
Schubert, S. & Henderson-Sellers, A. (1997). A statistical model to downscale local daily
temperature extremes from synoptic-scale atmospheric circulation patterns in the australian
region. Climate Dynamics, 13:223–234.
Schüpp, M. (1968). Kalender der wetter- und witterungslagen von 1955 bis 1967 im zentralen
alpengebiet. Veroeffentlichung der SMA,Zuerich, 11.
Semenov, M. (1997). Use of a stochastic weather generator in the development of climate
change scenarios. Climate Change, 35:397–414.
Stehlik, J. & Bardossy, A. (2002). Multivariate stochastic downscaling model for generating
daily precipitation series based on atmospheric circulation. Journal of Hydrology, 256:120–
141.
Trigo, R. & Palutikof, J. (1999). Simulation of daily temperatures for climate change scenarios
over portugal: a neural network model approach. Climate Research, 13:45–59.
Trigo, R. & Palutikof, J. (2001). Precipitation scenarios over iberia: a comparison between
direct gcm output and different downscaling techniques. Journal of Climate, 14:4422–4446.
Tweles, S. & Wobus, W. (1954). Verification of prognostic charts. bull. Amer. Meteor. Soc.,
35:455–463.
UNESCO (2003). World Water Development Report. The United Nations Educational, Scientific and Cultural Organization (UNESCO) and Berghahn Books.
von Storch, H., Zorita, E., & Cubasch, U. (1993). Downscaling of global climate change
estimates to regional scales: an application to iberian rainfall in wintertime. Journal of
Climate, 6:1161–1171.
Weichert, W. & Büger, G. (1998). Linear versus nonlinear techniques in downscaling. Climate
Research, 10:83–93.
130
Bibliography
Wigley, T., Jones, P., Briffa, K., & Smith, G. (1990). Obtaining sub-grid scale information
from coarse resolution general circulation model output. Journal of Geophysical Research,
95:1443–1453.
Wilby, R. & Wigley, T. (1994). Stochastic weather type simulation for regional climate change
impact assessment. Water Resources Research, 30:3395–3403.
Wilks, D. (1992). Adapting stochastic weather generation algorithms for climate change studies. Climatic Change, 22:67–84.
Wilks, D. (1995). Statistical Methods in the Atmospheric Sciences: An Introduction. Academic
Press.
Wilks, D. & Wilby, R. (1999). The weather generation game: a review of stochastic weather
models. Progress in Physical Geography, 23,3:329–357.
Williams, C. (1952). Sequences of wet and dry days considered in relation to the logarithmic
series. Quarterly Journal of the Royal Meteorological Society, 78:91–96.
Woolhiser, D. & Pegram, G. (1979). Maximum likelihood estimation of fourier coefficient to
describe seasonal variations of parameters in stochastic daily precipitation models. J. Appl.
Meteor., 18:34–42.
Yarnal, B. (1984). A procedure for the classification of synoptic weather maps from gridded
atmospheric pressure data. Comput Geosci, 10:397–410.
Zadeh, L. (1965). Fuzzy sets. Information and control, 8:338–353.
Zorita, E. & von Storch, H. (1999). The analog method as a simple statistical downscaling
technique: comparison with more complicated methods. Journal of Climate, 12:2474–2489.
131
Institut für Wasserbau
Universität Stuttgart
Pfaffenwaldring 61
70569 Stuttgart (Vaihingen)
Telefon (0711) 685 - 64717/64749/64752/64679
Telefax (0711) 685 - 67020 o. 64746 o. 64681
E-Mail: iws@iws.uni-stuttgart.de
http://www.iws.uni-stuttgart.de
Direktoren
Prof. Dr. rer. nat. Dr.-Ing. András Bárdossy
Prof. Dr.-Ing. Rainer Helmig
Prof. Dr.-Ing. Silke Wieprecht
Vorstand (Stand 1.10.2007)
Prof. Dr. rer. nat. Dr.-Ing. A. Bárdossy
Prof. Dr.-Ing. R. Helmig
Prof. Dr.-Ing. S. Wieprecht
Prof. Dr.-Ing. habil. B. Westrich
Jürgen Braun, PhD
Dr.-Ing. H. Class
Dr.-Ing. J. Götzinger (kommissarisch)
Dr.-Ing. S. Hartmann
Dr.-Ing. H.-P. Koschitzky
PD Dr.-Ing. W. Marx
Emeriti
Prof. Dr.-Ing. Dr.-Ing. E.h. Jürgen Giesecke
Prof. Dr.h.c. Dr.-Ing. E.h. Helmut Kobus, PhD
Lehrstuhl für Wasserbau und
Wassermengenwirtschaft
Leiter: Prof. Dr.-Ing. Silke Wieprecht
Stellv.: PD Dr.-Ing. Walter Marx, AOR
Lehrstuhl für Hydrologie und Geohydrologie
Leiter: Prof. Dr. rer. nat. Dr.-Ing. András Bárdossy
Stellv.: Dr.-Ing. Arne Färber
Lehrstuhl für Hydromechanik
und Hydrosystemmodellierung
Leiter: Prof. Dr.-Ing. Rainer Helmig
Stellv.: Dr.-Ing. Holger Class, AOR
VEGAS, Versuchseinrichtung zur
Grundwasser- und Altlastensanierung
Leitung: Jürgen Braun, PhD
Dr.-Ing. Hans-Peter Koschitzky, AD
Versuchsanstalt für Wasserbau
Leiter: apl. Prof. Dr.-Ing. Bernhard Westrich
Verzeichnis der Mitteilungshefte
1
Röhnisch, Arthur: Die Bemühungen um eine Wasserbauliche Versuchsanstalt an
der Technischen Hochschule Stuttgart,
und
Fattah Abouleid, Abdel: Beitrag zur Berechnung einer in lockeren Sand gerammten, zweifach verankerten Spundwand, 1963
2
Marotz, Günter: Beitrag zur Frage der Standfestigkeit von dichten Asphaltbelägen
im Großwasserbau, 1964
3
Gurr, Siegfried: Beitrag zur Berechnung zusammengesetzter ebener Flächentragwerke unter besonderer Berücksichtigung ebener Stauwände, mit Hilfe von
Randwert- und Lastwertmatrizen, 1965
4
Plica, Peter: Ein Beitrag zur Anwendung von Schalenkonstruktionen im Stahlwasserbau, und Petrikat, Kurt: Möglichkeiten und Grenzen des wasserbaulichen Versuchswesens, 1966
2
Institut für Wasserbau * Universität Stuttgart * IWS
5
Plate, Erich: Beitrag zur Bestimmung der Windgeschwindigkeitsverteilung in der
durch eine Wand gestörten bodennahen Luftschicht,
und
Röhnisch, Arthur; Marotz, Günter: Neue Baustoffe und Bauausführungen für den
Schutz der Böschungen und der Sohle von Kanälen, Flüssen und Häfen; Gestehungskosten und jeweilige Vorteile, sowie Unny, T.E.: Schwingungsuntersuchungen am Kegelstrahlschieber, 1967
6
Seiler, Erich: Die Ermittlung des Anlagenwertes der bundeseigenen Binnenschiffahrtsstraßen und Talsperren und des Anteils der Binnenschiffahrt an diesem Wert, 1967
7
Sonderheft anläßlich des 65. Geburtstages von Prof. Arthur Röhnisch mit Beiträgen von Benk, Dieter; Breitling, J.; Gurr, Siegfried; Haberhauer, Robert; Honekamp, Hermann; Kuz, Klaus Dieter; Marotz, Günter; Mayer-Vorfelder, Hans-Jörg;
Miller, Rudolf; Plate, Erich J.; Radomski, Helge; Schwarz, Helmut; Vollmer, Ernst;
Wildenhahn, Eberhard; 1967
8
Jumikis, Alfred: Beitrag zur experimentellen Untersuchung des Wassernachschubs
in einem gefrierenden Boden und die Beurteilung der Ergebnisse, 1968
9
Marotz, Günter: Technische Grundlagen einer Wasserspeicherung im natürlichen
Untergrund, 1968
10
Radomski, Helge: Untersuchungen über den Einfluß der Querschnittsform wellenförmiger Spundwände auf die statischen und rammtechnischen Eigenschaften,
1968
11
Schwarz, Helmut: Die Grenztragfähigkeit des Baugrundes bei Einwirkung vertikal
gezogener Ankerplatten als zweidimensionales Bruchproblem, 1969
12
Erbel, Klaus: Ein Beitrag zur Untersuchung der Metamorphose von Mittelgebirgsschneedecken unter besonderer Berücksichtigung eines Verfahrens zur Bestimmung der thermischen Schneequalität, 1969
13
Westhaus, Karl-Heinz: Der Strukturwandel in der Binnenschiffahrt und sein Einfluß
auf den Ausbau der Binnenschiffskanäle, 1969
14
Mayer-Vorfelder, Hans-Jörg: Ein Beitrag zur Berechnung des Erdwiderstandes unter Ansatz der logarithmischen Spirale als Gleitflächenfunktion, 1970
15
Schulz, Manfred: Berechnung des räumlichen Erddruckes auf die Wandung kreiszylindrischer Körper, 1970
16
Mobasseri, Manoutschehr: Die Rippenstützmauer. Konstruktion und Grenzen ihrer
Standsicherheit, 1970
17
Benk, Dieter: Ein Beitrag zum Betrieb und zur Bemessung von Hochwasserrückhaltebecken, 1970
3
18
Gàl, Attila: Bestimmung der mitschwingenden Wassermasse bei überströmten
Fischbauchklappen mit kreiszylindrischem Staublech, 1971,
19
Kuz, Klaus Dieter: Ein Beitrag zur Frage des Einsetzens von Kavitationserscheinungen in einer Düsenströmung bei Berücksichtigung der im Wasser gelösten Gase, 1971,
20
Schaak, Hartmut: Verteilleitungen von Wasserkraftanlagen, 1971
21
Sonderheft zur Eröffnung der neuen Versuchsanstalt des Instituts für Wasserbau
der Universität Stuttgart mit Beiträgen von Brombach, Hansjörg; Dirksen, Wolfram;
Gàl, Attila; Gerlach, Reinhard; Giesecke, Jürgen; Holthoff, Franz-Josef; Kuz, Klaus
Dieter; Marotz, Günter; Minor, Hans-Erwin; Petrikat, Kurt; Röhnisch, Arthur; Rueff,
Helge; Schwarz, Helmut; Vollmer, Ernst; Wildenhahn, Eberhard; 1972
22
Wang, Chung-su: Ein Beitrag zur Berechnung der Schwingungen an Kegelstrahlschiebern, 1972
23
Mayer-Vorfelder, Hans-Jörg:
Variationsverfahren, 1972
24
Minor, Hans-Erwin: Beitrag zur Bestimmung der Schwingungsanfachungsfunktionen überströmter Stauklappen, 1972,
25
Brombach, Hansjörg: Untersuchung strömungsmechanischer Elemente (Fluidik)
und die Möglichkeit der Anwendung von Wirbelkammerelementen im Wasserbau,
1972,
26
Wildenhahn, Eberhard: Beitrag zur Berechnung von Horizontalfilterbrunnen, 1972
27
Steinlein, Helmut: Die Eliminierung der Schwebstoffe aus Flußwasser zum Zweck
der unterirdischen Wasserspeicherung, gezeigt am Beispiel der Iller, 1972
28
Holthoff, Franz Josef: Die Überwindung großer Hubhöhen in der Binnenschiffahrt
durch Schwimmerhebewerke, 1973
29
Röder, Karl: Einwirkungen aus Baugrundbewegungen auf trog- und kastenförmige
Konstruktionen des Wasser- und Tunnelbaues, 1973
30
Kretschmer, Heinz: Die Bemessung von Bogenstaumauern in Abhängigkeit von
der Talform, 1973
31
Honekamp, Hermann: Beitrag zur Berechnung der Montage von Unterwasserpipelines, 1973
32
Giesecke, Jürgen: Die Wirbelkammertriode als neuartiges Steuerorgan im Wasserbau, und Brombach, Hansjörg: Entwicklung, Bauformen, Wirkungsweise und
Steuereigenschaften von Wirbelkammerverstärkern, 1974
33
Rueff, Helge: Untersuchung der schwingungserregenden Kräfte an zwei hintereinander angeordneten Tiefschützen unter besonderer Berücksichtigung von Kavitation, 1974
Erdwiderstandsbeiwerte
nach
dem
Ohde-
4
34
Röhnisch, Arthur: Einpreßversuche mit Zementmörtel für Spannbeton - Vergleich
der Ergebnisse von Modellversuchen mit Ausführungen in Hüllwellrohren, 1975
35
Sonderheft anläßlich des 65. Geburtstages von Prof. Dr.-Ing. Kurt Petrikat mit Beiträgen von: Brombach, Hansjörg; Erbel, Klaus; Flinspach, Dieter; Fischer jr., Richard; Gàl, Attila; Gerlach, Reinhard; Giesecke, Jürgen; Haberhauer, Robert; Hafner Edzard; Hausenblas, Bernhard; Horlacher, Hans-Burkhard; Hutarew, Andreas;
Knoll, Manfred; Krummet, Ralph; Marotz, Günter; Merkle, Theodor; Miller, Christoph; Minor, Hans-Erwin; Neumayer, Hans; Rao, Syamala; Rath, Paul; Rueff, Helge; Ruppert, Jürgen; Schwarz, Wolfgang; Topal-Gökceli, Mehmet; Vollmer, Ernst;
Wang, Chung-su; Weber, Hans-Georg; 1975
36
Berger, Jochum: Beitrag zur Berechnung des Spannungszustandes in rotationssymmetrisch belasteten Kugelschalen veränderlicher Wandstärke unter Gas- und
Flüssigkeitsdruck durch Integration schwach singulärer Differentialgleichungen,
1975
37
Dirksen, Wolfram: Berechnung instationärer Abflußvorgänge in gestauten Gerinnen mittels Differenzenverfahren und die Anwendung auf Hochwasserrückhaltebecken, 1976
38
Horlacher, Hans-Burkhard: Berechnung instationärer Temperatur- und Wärmespannungsfelder in langen mehrschichtigen Hohlzylindern, 1976
39
Hafner, Edzard: Untersuchung der hydrodynamischen Kräfte auf Baukörper im
Tiefwasserbereich des Meeres, 1977, ISBN 3-921694-39-6
40
Ruppert, Jürgen: Über den Axialwirbelkammerverstärker für den Einsatz im Wasserbau, 1977, ISBN 3-921694-40-X
41
Hutarew, Andreas: Beitrag zur Beeinflußbarkeit des Sauerstoffgehalts in Fließgewässern an Abstürzen und Wehren, 1977, ISBN 3-921694-41-8,
42
Miller, Christoph: Ein Beitrag zur Bestimmung der schwingungserregenden Kräfte
an unterströmten Wehren, 1977, ISBN 3-921694-42-6
43
Schwarz, Wolfgang: Druckstoßberechnung unter Berücksichtigung der Radial- und
Längsverschiebungen der Rohrwandung, 1978, ISBN 3-921694-43-4
44
Kinzelbach, Wolfgang: Numerische Untersuchungen über den optimalen Einsatz
variabler Kühlsysteme einer Kraftwerkskette am Beispiel Oberrhein, 1978,
ISBN 3-921694-44-2
45
Barczewski, Baldur: Neue Meßmethoden für Wasser-Luftgemische und deren Anwendung auf zweiphasige Auftriebsstrahlen, 1979, ISBN 3-921694-45-0
46
Neumayer, Hans: Untersuchung der Strömungsvorgänge in radialen Wirbelkammerverstärkern, 1979, ISBN 3-921694-46-9
47
Elalfy, Youssef-Elhassan: Untersuchung der Strömungsvorgänge in Wirbelkammerdioden und -drosseln, 1979, ISBN 3-921694-47-7
5
48
Brombach, Hansjörg: Automatisierung der Bewirtschaftung von Wasserspeichern,
1981, ISBN 3-921694-48-5
49
Geldner, Peter: Deterministische und stochastische Methoden zur Bestimmung der
Selbstdichtung von Gewässern, 1981, ISBN 3-921694-49-3,
50
Mehlhorn, Hans: Temperaturveränderungen im Grundwasser durch Brauchwassereinleitungen, 1982, ISBN 3-921694-50-7,
51
Hafner, Edzard: Rohrleitungen und Behälter im Meer, 1983, ISBN 3-921694-51-5
52
Rinnert, Bernd: Hydrodynamische Dispersion in porösen Medien: Einfluß von Dichteunterschieden auf die Vertikalvermischung in horizontaler Strömung, 1983, ISBN
3-921694-52-3,
53
Lindner, Wulf: Steuerung von Grundwasserentnahmen unter Einhaltung ökologischer Kriterien, 1983, ISBN 3-921694-53-1,
54
Herr, Michael; Herzer, Jörg; Kinzelbach, Wolfgang; Kobus, Helmut; Rinnert, Bernd:
Methoden zur rechnerischen Erfassung und hydraulischen Sanierung von Grundwasserkontaminationen, 1983, ISBN 3-921694-54-X
55
Schmitt, Paul: Wege zur Automatisierung der Niederschlagsermittlung, 1984, ISBN
3-921694-55-8,
56
Müller, Peter: Transport und selektive Sedimentation von Schwebstoffen bei gestautem Abfluß, 1985, ISBN 3-921694-56-6
57
El-Qawasmeh, Fuad: Möglichkeiten und Grenzen der Tropfbewässerung unter besonderer Berücksichtigung der Verstopfungsanfälligkeit der Tropfelemente, 1985,
ISBN 3-921694-57-4,
58
Kirchenbaur, Klaus: Mikroprozessorgesteuerte Erfassung instationärer Druckfelder
am Beispiel seegangsbelasteter Baukörper, 1985, ISBN 3-921694-58-2
59
Kobus, Helmut (Hrsg.): Modellierung des großräumigen Wärme- und Schadstofftransports im Grundwasser, Tätigkeitsbericht 1984/85 (DFG-Forschergruppe an
den Universitäten Hohenheim, Karlsruhe und Stuttgart), 1985,
ISBN 3-921694-59-0,
60
Spitz, Karlheinz: Dispersion in porösen Medien: Einfluß von Inhomogenitäten und
Dichteunterschieden, 1985, ISBN 3-921694-60-4,
61
Kobus, Helmut: An Introduction to Air-Water Flows in Hydraulics, 1985,
ISBN 3-921694-61-2
62
Kaleris, Vassilios: Erfassung des Austausches von Oberflächen- und Grundwasser
in horizontalebenen Grundwassermodellen, 1986, ISBN 3-921694-62-0
63
Herr, Michael: Grundlagen der hydraulischen Sanierung verunreinigter Porengrundwasserleiter, 1987, ISBN 3-921694-63-9
6
64
Marx, Walter: Berechnung von Temperatur und Spannung in Massenbeton infolge
Hydratation, 1987, ISBN 3-921694-64-7
65
Koschitzky, Hans-Peter: Dimensionierungskonzept für Sohlbelüfter in Schußrinnen
zur Vermeidung von Kavitationsschäden, 1987, ISBN 3-921694-65-5
66
Kobus, Helmut (Hrsg.): Modellierung des großräumigen Wärme- und Schadstofftransports im Grundwasser, Tätigkeitsbericht 1986/87 (DFG-Forschergruppe an
den Universitäten Hohenheim, Karlsruhe und Stuttgart) 1987, ISBN 3-921694-66-3
67
Söll, Thomas: Berechnungsverfahren zur Abschätzung anthropogener Temperaturanomalien im Grundwasser, 1988, ISBN 3-921694-67-1
68
Dittrich, Andreas; Westrich, Bernd: Bodenseeufererosion, Bestandsaufnahme und
Bewertung, 1988, ISBN 3-921694-68-X,
69
Huwe, Bernd; van der Ploeg, Rienk R.: Modelle zur Simulation des Stickstoffhaushaltes von Standorten mit unterschiedlicher landwirtschaftlicher Nutzung, 1988,
ISBN 3-921694-69-8,
70
Stephan, Karl: Integration elliptischer Funktionen, 1988, ISBN 3-921694-70-1
71
Kobus, Helmut; Zilliox, Lothaire (Hrsg.): Nitratbelastung des Grundwassers, Auswirkungen der Landwirtschaft auf die Grundwasser- und Rohwasserbeschaffenheit
und Maßnahmen zum Schutz des Grundwassers. Vorträge des deutsch-französischen Kolloquiums am 6. Oktober 1988, Universitäten Stuttgart und Louis Pasteur Strasbourg (Vorträge in deutsch oder französisch, Kurzfassungen zweisprachig), 1988, ISBN 3-921694-71-X
72
Soyeaux, Renald: Unterströmung von Stauanlagen auf klüftigem Untergrund unter
Berücksichtigung laminarer und turbulenter Fließzustände,1991,
ISBN 3-921694-72-8
73
Kohane, Roberto: Berechnungsmethoden für Hochwasserabfluß in Fließgewässern mit überströmten Vorländern, 1991, ISBN 3-921694-73-6
74
Hassinger, Reinhard: Beitrag zur Hydraulik und Bemessung von Blocksteinrampen
in flexibler Bauweise, 1991, ISBN 3-921694-74-4,
75
Schäfer, Gerhard: Einfluß von Schichtenstrukturen und lokalen Einlagerungen auf
die Längsdispersion in Porengrundwasserleitern, 1991, ISBN 3-921694-75-2
76
Giesecke, Jürgen: Vorträge, Wasserwirtschaft in stark besiedelten Regionen; Umweltforschung mit Schwerpunkt Wasserwirtschaft, 1991, ISBN 3-921694-76-0
77
Huwe, Bernd: Deterministische und stochastische Ansätze zur Modellierung des
Stickstoffhaushalts landwirtschaftlich genutzter Flächen auf unterschiedlichem
Skalenniveau, 1992, ISBN 3-921694-77-9,
78
Rommel, Michael: Verwendung von Kluftdaten zur realitätsnahen Generierung von
Kluftnetzen mit anschließender laminar-turbulenter Strömungsberechnung, 1993,
ISBN 3-92 1694-78-7
7
79
Marschall, Paul: Die Ermittlung lokaler Stofffrachten im Grundwasser mit Hilfe von
Einbohrloch-Meßverfahren, 1993, ISBN 3-921694-79-5,
80
Ptak, Thomas: Stofftransport in heterogenen Porenaquiferen: Felduntersuchungen
und stochastische Modellierung, 1993, ISBN 3-921694-80-9,
81
Haakh, Frieder: Transientes Strömungsverhalten in Wirbelkammern, 1993,
ISBN 3-921694-81-7
82
Kobus, Helmut; Cirpka, Olaf; Barczewski, Baldur; Koschitzky, Hans-Peter: Versucheinrichtung zur Grundwasser und Altlastensanierung VEGAS, Konzeption und
Programmrahmen, 1993, ISBN 3-921694-82-5
83
Zang, Weidong: Optimaler Echtzeit-Betrieb eines Speichers mit aktueller Abflußregenerierung, 1994, ISBN 3-921694-83-3,
84
Franke, Hans-Jörg: Stochastische Modellierung eines flächenhaften Stoffeintrages
und Transports in Grundwasser am Beispiel der Pflanzenschutzmittelproblematik,
1995, ISBN 3-921694-84-1
85
Lang, Ulrich: Simulation regionaler Strömungs- und Transportvorgänge in Karstaquiferen mit Hilfe des Doppelkontinuum-Ansatzes: Methodenentwicklung und Parameteridentifikation, 1995, ISBN 3-921694-85-X,
86
Helmig, Rainer: Einführung in die Numerischen Methoden der Hydromechanik,
1996, ISBN 3-921694-86-8,
87
Cirpka, Olaf: CONTRACT: A Numerical Tool for Contaminant Transport and
Chemical Transformations - Theory and Program Documentation -, 1996,
ISBN 3-921694-87-6
88
Haberlandt, Uwe: Stochastische Synthese und Regionalisierung des Niederschlages für Schmutzfrachtberechnungen, 1996, ISBN 3-921694-88-4
89
Croisé, Jean: Extraktion von flüchtigen Chemikalien aus natürlichen Lockergesteinen mittels erzwungener Luftströmung, 1996, ISBN 3-921694-89-2,
90
Jorde, Klaus: Ökologisch begründete, dynamische Mindestwasserregelungen bei
Ausleitungskraftwerken, 1997, ISBN 3-921694-90-6,
91
Helmig, Rainer: Gekoppelte Strömungs- und Transportprozesse im Untergrund Ein Beitrag zur Hydrosystemmodellierung-, 1998, ISBN 3-921694-91-4
92
Emmert, Martin: Numerische Modellierung nichtisothermer Gas-Wasser Systeme
in porösen Medien, 1997, ISBN 3-921694-92-2
93
Kern, Ulrich: Transport von Schweb- und Schadstoffen in staugeregelten Fließgewässern am Beispiel des Neckars, 1997, ISBN 3-921694-93-0,
94
Förster, Georg: Druckstoßdämpfung durch große Luftblasen in Hochpunkten von
Rohrleitungen 1997, ISBN 3-921694-94-9
8
95
Cirpka, Olaf: Numerische Methoden zur Simulation des reaktiven Mehrkomponententransports im Grundwasser, 1997, ISBN 3-921694-95-7,
96
Färber, Arne: Wärmetransport in der ungesättigten Bodenzone: Entwicklung einer
thermischen In-situ-Sanierungstechnologie, 1997, ISBN 3-921694-96-5
97
Betz, Christoph: Wasserdampfdestillation von Schadstoffen im porösen Medium:
Entwicklung einer thermischen In-situ-Sanierungstechnologie, 1998,
ISBN 3-921694-97-3
98
Xu, Yichun: Numerical Modeling of Suspended Sediment Transport in Rivers,
1998, ISBN 3-921694-98-1,
99
Wüst, Wolfgang: Geochemische Untersuchungen zur Sanierung CKWkontaminierter Aquifere mit Fe(0)-Reaktionswänden, 2000, ISBN 3-933761-02-2
100 Sheta, Hussam: Simulation von Mehrphasenvorgängen in porösen Medien unter
Einbeziehung von Hysterese-Effekten, 2000, ISBN 3-933761-03-4
101 Ayros, Edwin: Regionalisierung extremer Abflüsse auf der Grundlage statistischer
Verfahren, 2000, ISBN 3-933761-04-2,
102 Huber, Ralf: Compositional Multiphase Flow and Transport in Heterogeneous Porous Media, 2000, ISBN 3-933761-05-0
103 Braun, Christopherus: Ein Upscaling-Verfahren für Mehrphasenströmungen in porösen Medien, 2000, ISBN 3-933761-06-9
104 Hofmann, Bernd: Entwicklung eines rechnergestützten Managementsystems zur
Beurteilung von Grundwasserschadensfällen, 2000, ISBN 3-933761-07-7
105 Class, Holger: Theorie und numerische Modellierung nichtisothermer Mehrphasenprozesse in NAPL-kontaminierten porösen Medien, 2001,
ISBN 3-933761-08-5
106 Schmidt, Reinhard: Wasserdampf- und Heißluftinjektion zur thermischen Sanierung kontaminierter Standorte, 2001, ISBN 3-933761-09-3
107 Josef, Reinhold:, Schadstoffextraktion mit hydraulischen Sanierungsverfahren unter Anwendung von grenzflächenaktiven Stoffen, 2001, ISBN 3-933761-10-7
108 Schneider, Matthias: Habitat- und Abflussmodellierung für Fließgewässer mit unscharfen Berechnungsansätzen, 2001, ISBN 3-933761-11-5
109 Rathgeb, Andreas: Hydrodynamische Bemessungsgrundlagen für Lockerdeckwerke an überströmbaren Erddämmen, 2001, ISBN 3-933761-12-3
110 Lang, Stefan: Parallele numerische Simulation instätionärer Probleme mit adaptiven Methoden auf unstrukturierten Gittern, 2001, ISBN 3-933761-13-1
9
111 Appt, Jochen; Stumpp Simone: Die Bodensee-Messkampagne 2001, IWS/CWR
Lake Constance Measurement Program 2001, 2002, ISBN 3-933761-14-X
112 Heimerl, Stephan: Systematische Beurteilung von Wasserkraftprojekten, 2002,
ISBN 3-933761-15-8
113 Iqbal, Amin: On the Management and Salinity Control of Drip Irrigation, 2002, ISBN
3-933761-16-6
114 Silberhorn-Hemminger, Annette: Modellierung von Kluftaquifersystemen: Geostatistische Analyse und deterministisch-stochastische Kluftgenerierung, 2002, ISBN
3-933761-17-4
115 Winkler, Angela: Prozesse des Wärme- und Stofftransports bei der In-situSanierung mit festen Wärmequellen, 2003, ISBN 3-933761-18-2
116 Marx, Walter: Wasserkraft, Bewässerung, Umwelt - Planungs- und Bewertungsschwerpunkte der Wasserbewirtschaftung, 2003, ISBN 3-933761-19-0
117 Hinkelmann, Reinhard: Efficient Numerical Methods and Information-Processing
Techniques in Environment Water, 2003, ISBN 3-933761-20-4
118 Samaniego-Eguiguren, Luis Eduardo: Hydrological Consequences of Land Use /
Land Cover and Climatic Changes in Mesoscale Catchments, 2003,
ISBN 3-933761-21-2
119 Neunhäuserer, Lina: Diskretisierungsansätze zur Modellierung von Strömungsund Transportprozessen in geklüftet-porösen Medien, 2003, ISBN 3-933761-22-0
120 Paul, Maren: Simulation of Two-Phase Flow in Heterogeneous Poros Media with
Adaptive Methods, 2003, ISBN 3-933761-23-9
121 Ehret, Uwe: Rainfall and Flood Nowcasting in Small Catchments using Weather
Radar, 2003, ISBN 3-933761-24-7
122 Haag, Ingo: Der Sauerstoffhaushalt staugeregelter Flüsse am Beispiel des Neckars - Analysen, Experimente, Simulationen -, 2003, ISBN 3-933761-25-5
123 Appt, Jochen: Analysis of Basin-Scale Internal Waves in Upper Lake Constance,
2003, ISBN 3-933761-26-3
124 Hrsg.: Schrenk, Volker; Batereau, Katrin; Barczewski, Baldur; Weber, Karolin und
Koschitzky, Hans-Peter: Symposium Ressource Fläche und VEGAS - Statuskolloquium 2003, 30. September und 1. Oktober 2003, 2003, ISBN 3-933761-27-1
125 Omar Khalil Ouda: Optimisation of Agricultural Water Use: A Decision Support
System for the Gaza Strip, 2003, ISBN 3-933761-28-0
126 Batereau, Katrin: Sensorbasierte Bodenluftmessung zur Vor-Ort-Erkundung von
Schadensherden im Untergrund, 2004, ISBN 3-933761-29-8
10
127 Witt, Oliver: Erosionsstabilität von Gewässersedimenten mit Auswirkung auf den
Stofftransport bei Hochwasser am Beispiel ausgewählter Stauhaltungen des Oberrheins, 2004, ISBN 3-933761-30-1
128 Jakobs, Hartmut: Simulation nicht-isothermer Gas-Wasser-Prozesse in komplexen
Kluft-Matrix-Systemen, 2004, ISBN 3-933761-31-X
129 Li, Chen-Chien: Deterministisch-stochastisches Berechnungskonzept zur Beurteilung der Auswirkungen erosiver Hochwasserereignisse in Flussstauhaltungen,
2004, ISBN 3-933761-32-8
130 Reichenberger, Volker; Helmig, Rainer; Jakobs, Hartmut; Bastian, Peter; Niessner,
Jennifer: Complex Gas-Water Processes in Discrete Fracture-Matrix Systems: Upscaling, Mass-Conservative Discretization and Efficient Multilevel Solution, 2004,
ISBN 3-933761-33-6
131 Hrsg.: Barczewski, Baldur; Koschitzky, Hans-Peter; Weber, Karolin; Wege, Ralf:
VEGAS - Statuskolloquium 2004, Tagungsband zur Veranstaltung am 05. Oktober
2004 an der Universität Stuttgart, Campus Stuttgart-Vaihingen, 2004, ISBN 3933761-34-4
132 Asie, Kemal Jabir: Finite Volume Models for Multiphase Multicomponent Flow
through Porous Media. 2005, ISBN 3-933761-35-2
133 Jacoub, George: Development of a 2-D Numerical Module for Particulate Contaminant Transport in Flood Retention Reservoirs and Impounded Rivers, 2004,
ISBN 3-933761-36-0
134 Nowak, Wolfgang: Geostatistical Methods for the Identification of Flow and Transport Parameters in the Subsurface, 2005, ISBN 3-933761-37-9
135 Süß, Mia: Analysis of the influence of structures and boundaries on flow and
transport processes in fractured porous media, 2005, ISBN 3-933761-38-7
136 Jose, Surabhin Chackiath: Experimental Investigations on Longitudinal Dispersive
Mixing in Heterogeneous Aquifers, 2005, ISBN: 3-933761-39-5
137 Filiz, Fulya: Linking Large-Scale Meteorological Conditions to Floods in Mesoscale
Catchments, 2005, ISBN 3-933761-40-9
138 Qin, Minghao: Wirklichkeitsnahe und recheneffiziente Ermittlung von Temperatur
und Spannungen bei großen RCC-Staumauern, 2005, ISBN 3-933761-41-7
139 Kobayashi, Kenichiro: Optimization Methods for Multiphase Systems in the Subsurface - Application to Methane Migration in Coal Mining Areas, 2005,
ISBN 3-933761-42-5
140 Rahman, Md. Arifur: Experimental Investigations on Transverse Dispersive Mixing
in Heterogeneous Porous Media, 2005, ISBN 3-933761-43-3
11
141 Schrenk, Volker: Ökobilanzen zur Bewertung von Altlastensanierungsmaßnahmen,
2005, ISBN 3-933761-44-1
142 Hundecha, Hirpa Yeshewatesfa: Regionalization of Parameters of a Conceptual
Rainfall-Runoff Model, 2005, ISBN: 3-933761-45-X
143 Wege, Ralf: Untersuchungs- und Überwachungsmethoden für die Beurteilung natürlicher Selbstreinigungsprozesse im Grundwasser, 2005, ISBN 3-933761-46-8
144 Breiting, Thomas: Techniken und Methoden der Hydroinformatik - Modellierung
von komplexen Hydrosystemen im Untergrund, 2006, 3-933761-47-6
145 Hrsg.: Braun, Jürgen; Koschitzky, Hans-Peter; Müller, Martin: Ressource Untergrund: 10 Jahre VEGAS: Forschung und Technologieentwicklung zum Schutz von
Grundwasser und Boden, Tagungsband zur Veranstaltung am 28. und 29. September 2005 an der Universität Stuttgart, Campus Stuttgart-Vaihingen, 2005, ISBN
3-933761-48-4
146 Rojanschi, Vlad: Abflusskonzentration in mesoskaligen Einzugsgebieten unter
Berücksichtigung des Sickerraumes, 2006, ISBN 3-933761-49-2
147 Winkler, Nina Simone: Optimierung der Steuerung von Hochwasserrückhaltebecken-systemen, 2006, ISBN 3-933761-50-6
148 Wolf, Jens: Räumlich differenzierte Modellierung der Grundwasserströmung alluvialer Aquifere für mesoskalige Einzugsgebiete, 2006, ISBN: 3-933761-51-4
149 Kohler, Beate: Externe Effekte der Laufwasserkraftnutzung, 2006,
ISBN 3-933761-52-2
150 Hrsg.: Braun, Jürgen; Koschitzky, Hans-Peter; Stuhrmann, Matthias: VEGASStatuskolloquium 2006, Tagungsband zur Veranstaltung am 28. September 2006
an der Universität Stuttgart, Campus Stuttgart-Vaihingen, 2006,
ISBN 3-933761-53-0
151 Niessner, Jennifer: Multi-Scale Modeling of Multi-Phase - Multi-Component Processes in Heterogeneous Porous Media, 2006, ISBN 3-933761-54-9
152 Fischer, Markus: Beanspruchung eingeerdeter Rohrleitungen infolge Austrocknung
bindiger Böden, 2006, ISBN 3-933761-55-7
153 Schneck, Alexander: Optimierung der Grundwasserbewirtschaftung unter Berücksichtigung der Belange der Wasserversorgung, der Landwirtschaft und des Naturschutzes, 2006, ISBN 3-933761-56-5
154 Das, Tapash: The Impact of Spatial Variability of Precipitation on the Predictive
Uncertainty of Hydrological Models, 2006, ISBN 3-933761-57-3
155 Bielinski, Andreas: Numerical Simulation of CO2 sequestration in geological formations, 2007, ISBN 3-933761-58-1
12
156 Mödinger, Jens: Entwicklung eines Bewertungs- und Entscheidungsunterstützungssystems für eine nachhaltige regionale Grundwasserbewirtschaftung, 2006,
ISBN 3-933761-60-3
157 Manthey, Sabine: Two-phase flow processes with dynamic effects in porous
media - parameter estimation and simulation, 2007, ISBN 3-933761-61-1
158 Pozos Estrada, Oscar: Investigation on the Effects of Entrained Air in Pipelines,
2007, ISBN 3-933761-62-X
159 Ochs, Steffen Oliver: Steam injection into saturated porous media – process
analysis including experimental and numerical investigations, 2007,
ISBN 3-933761-63-8
160 Marx, Andreas: Einsatz gekoppelter Modelle und Wetterradar zur Abschätzung
von Niederschlagsintensitäten und zur Abflussvorhersage, 2007,
ISBN 3-933761-64-6
161 Hartmann, Gabriele Maria: Investigation of Evapotranspiration Concepts in Hydrological Modelling for Climate Change Impact Assessment, 2007,
ISBN 3-933761-65-4
162 Kebede Gurmessa, Tesfaye: Numerical Investigation on Flow and Transport Characteristics to Improve Long-Term Simulation of Reservoir Sedimentation, 2007,
ISBN 3-933761-66-2
163 Trifković, Aleksandar: Multi-objective and Risk-based Modelling Methodology for
Planning, Design and Operation of Water Supply Systems, 2007,
ISBN 3-933761-67-0
164 Götzinger, Jens: Distributed Conceptual Hydrological Modelling - Simulation of
Climate, Land Use Change Impact and Uncertainty Analysis, 2007,
ISBN 3-933761-68-9
165 Hrsg.: Braun, Jürgen; Koschitzky, Hans-Peter; Stuhrmann, Matthias: VEGAS –
Kolloquium 2007, Tagungsband zur Veranstaltung am 26. September 2007 an der
Universität Stuttgart, Campus Stuttgart-Vaihingen, 2007, ISBN 3-933761-69-7
166 Freeman, Beau: Modernization Criteria Assessment for Water Resources Planning; Klamath Irrigation Project, U.S., 2008, ISBN 3-933761-70-0
167 Dreher, Thomas: Selektive Sedimentation von Feinstschwebstoffen in Wechselwirkung mit wandnahen turbulenten Strömungsbedingungen, 2008,
ISBN 3-933761-71-9
168 Yang, Wei: Discrete-continuous Downscaling Model for Generating Daily Precipitation Time Series, 2008, ISBN 3-933761-72-7
Die Mitteilungshefte ab dem Jahr 2005 stehen als pdf-Datei über die Homepage des Instituts: www.iws.uni-stuttgart.de zur Verfügung.

Heft 168 Wei Yang Discrete-Continuous Downscaling Model for

Transcription

Similar documents

Heft 121 Uwe Ehret Rainfall - Institut für Wasser

Statistische Verfahren zur Auswertung von Klimadaten aus Modell

komplette Bachelorarbeit - Hessisches Landesamt für Naturschutz

- Department of Simulation and Graphics

(PDF / 617 kB) - Forschungszentrum Jülich