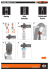δ Optimization of automated gas sample collection and IRMS analysis of

1
2
3
4
Optimization of automated gas sample collection and IRMS
analysis of δ 13C of CO2 in air
Matthias J. Zeeman1 , Roland A. Werner1 , Werner Eugster1 , Rolf T. W. Siegwolf2 , Günther Wehrle2 ,
Joachim Mohn3 , Nina Buchmann1
1 Institute
8
of Plant Sciences, ETH Zurich, Universitaetsstrasse 2, CH–8092 Zurich, Switzerland
of Atmospheric Chemistry, Paul Scherrer Institute, Bachstrasse 1, CH–5232 Villingen, Switzerland
3 Laboratory for Air Pollution & Environmental Technology, Empa, Überlandstrasse 129, CH–8600 Dübendorf,
Switzerland
9
Abstract
5
6
7
10
11
12
13
14
15
16
17
2 Laboratory
The application of 13 C/12 C in ecosystem–scale tracer models for CO2 in air requires accurate measurements of mixing ratios and stable isotope ratios of CO2 . To increase measurement reliability and
data intercomparability as well as to shorten analysis times, we have improved an existing field sampling
setup with portable air sampling units and developed a laboratory setup for analysis of δ 13 C of CO2 in
air by isotope ratio mass spectrometry (IRMS). The changes consist of (a) optimization of sample and
standard gas flow paths, (b) additional software configuration and (c) automation of liquid nitrogen refilling for the cryogenic trap. We achieved a precision better than 0.1‡ and an accuracy of 0.11±0.04‡
for δ 13 C of CO2 in air and unattended operation of measurement sequences up to 12 hours.
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
The interest in the global atmospheric carbon cycle has intensified as a response to reported trends in global climate change. These
trends are primarily related to atmospheric increases in greenhouse gas concentrations. 1 On
the global average, carbon dioxide (CO2 ) plays
the most important role and thus ecosystem oriented research has particularly focused on CO2 .
The potential use of the stable isotope ratios of
CO2 (e.g. 13 C/12 C, 18 O/16 O) in ecosystem–scale
atmosphere–biosphere process studies has often
been highlighted and is believed to be a powerful tool for carbon cycle studies, in particular to
disentangle ecosystem flux components.e.g. 2–7 It is
commonly used to quantify mixing contributions
from sources with differing isotopic compositions. 8,9 However, this requires accurate measurements of both CO2 mixing ratios and isotopic composition in order to be useable in ecosystem–scale
tracer model approaches. 4,10,11 On local (species
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
∗ Correspondence
to ecosystem) scales this can be quite a challenge;
CO2 mixing ratios and isotopic composition in the
air close to the vegetation are known to fluctuate strongly, i.e. on short time scales (seconds to
hours), especially under less turbulent atmospheric
conditions due to accumulation of CO2 . Moreover,
with conventional flask sampling the measurement
strategy is mostly limited to discrete sampling, and
typically these samples need to be transferred to a
distant laboratory for analysis by an Isotope Ratio
Mass Spectrometer, so the insight into ecosystem
processes is hampered by technical and logistical
constraints.
In this paper, we aim to optimize and extensively test air sampling and analysis of stable
carbon and oxygen isotope ratios in atmospheric
CO2 for stable isotope studies at the ecosystem
level. The setup described here has been successfully used for grassland ecosystem studies in
Switzerland and intercomparisons of stable iso-
to: MJ Zeeman, ETH Zurich, Institute of Plant Sciences, Universitaetsstrasse 2, CH–8092 Zurich, Switzerland, Email: matthias.zeeman@ipw.agrl.ethz.ch, Phone: +41 44 632 81 96, Fax: +41 44 632 11 53
1
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
tope ratio instrumentation (e.g. a comparison of
a quantum cascade laser based absorption spectrometer, a field-deployable Fourier transform infrared spectrometer and an Isotope Ratio Mass
Spectrometer).e.g. 12–14 The basic considerations
for the chosen measurement approach haves been
(a) the collection of samples at multiple locations
for (b) sample measurements by laboratory based
high precision Isotope Ratio Mass Spectrometer.
The most important implication of this approach
is that the conditions (e.g. temperature, pressure) might be different between location of sample collection and the laboratory. Thus, gas samples might be contaminated during the storage period between sampling and analysis, which is especially likely if samples are collected at higher
altitudes under reduced ambient pressure. 15–18 For
time series analysis, e.g. to understand diurnal cycles or effects of weather events, samples
or series of samples are repetitively collected at
equally spaced time intervals. If a Keeling plot approach (inverse [CO2 ] related to isotope δ –value)
is used, the accuracy of y–axis intercepts is directly related to the precision and accuracy of the
measurements.cf. 4 Thus, the analysis must be as
accurate and precise as possible, deviations should
be on the order of 0.1‡ for δ 13 C at most.
To achieve our aims, we have substantially
improved existing gas sampling equipment previously described by Theis et al. 19 and developed a
new Isotope Ratio Mass Spectrometer setup, programming and measurement routines for δ 13 C of
CO2 in air. An overview of this improved setup
is shown in Figure 1 for both field and laboratory
setup. An important part of these improvements
was to optimize the automation of the operations
during sampling and isotope ratio analysis to allow
for accurate timings and increased reproducibility.
Thus, our objectives were to 1) apply digital communication protocols between the sampling unit
and the control computer to store status information from the sampling unit in order to eliminated
the potential error of sample misidenfication.cf. 20
2) We wanted to increase precision and reliability
of the IRMS measurements for CO2 in air samples and optimize sample preparation steps. 3) We
wanted to reduce the time required per IRMS analysis of a CO2 in air sample to increase throughput
in the laboratory and reduce storage times of the
samples.
109
Methodology
110
Field setup
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
2
Three devices are used in our field setup (Fig. 1),
consisting of an home-built air inlet selection unit,
followed by an InfraRed Gas Analyzer (IRGA)
for CO2 mixing ratios (model LI-840, LI-COR,
Lincoln, Nebraska, USA) and a sample manifold at the end. This sample manifold is a
modified and improved version of the device
termed Automated Sampler of Air (ASA) by Theis
et al. 19 . It contains 33 glass flasks sample containers connected to three multiport Valco-valves
(EMTMA2ST12MWE, VICI, Schenkon, Switzerland) allowing independent filling of each individual sample container with sample air. We continue to use the abbreviation “ASA” to refer to the
portable air sampling unit described here, because
its key components (the Valvo-valves) and its function as sample manifold have not changed with
respect to the Theis et al. 19 version, despite the
modifications described here.
During field deployment, a single inlet is selected from a series of continuously purged air inlets (Synflex™Type 1300, formerly known as Dekabon™, Gembloux SA/NV, Belgium; ID 4 mm,
≈ 1 L min−1 ). After a particle filter (Gelman,
LI-COR), a T-split diverts the airflow (a) to the
IRGA and a subsequent small pump (DC12/8FK,
Fürgut GmbH, Germany) inside the inlet selection unit, and (b) to an ASA sample inlet. The
flow through the IRGA is kept at a continuous
rate of 0.9 L min−1 (Fig. 1), within the manufacturer supplied specifications for the IRGA. Once
inside the ASA (Fig. 2), the sample air is pushed
by a pump, diverted on activation of a solenoid
valve (EVT307-5D0-02F-Q, SMC, Weisslingen,
Switzerland) through a drying column containing
magnesium perchlorate (Fluka, Switzerland) and
is filtered (SS-4FW-2, Swagelok, USA) before being pushed further through 300 mL glass flasks
(Ernst Keller & Co AG, Basel, Switzerland) or
10 mL stainless steel loops (SL10KSTP, VICI,
Schenkon, Switzerland) connected to the multiport
Valco-valves with ≈ 0.9 L min−1 . At one of the 12
positions of each Valco-valve a short stainless steel
capillary is used as low volume bypass to allow
aligning multiple Valco-valves in series, typically
three or four per ASA. To create an over-pressure
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
of at least 50 kPa in the sample containers, we
changed the original Theis et al. 19 design and the
position of the Teflon membrane pump (N811KDC, KNF, Germany) in combination with a poppet
check valve (SS-6C-MM-1, Swagelok, USA) and
an adjustable flow meter (V-100, Vögtlin, Switzerland) at the exit. By having pressurized sample containers, the chance of contamination during transport and laboratory analysis is minimized.
In the laboratory (Zurich, 400 m above sea level,
a.s.l.), the pressure excess (pressure above ambient) directly after the pump inside the ASA (Fig. 2)
was typically found to be ≈ 90 kPa and ≈ 50 kPa
before the adjustable flow meter. This is sufficient for the collection of samples at alpine locations (e.g. >2000 m a.s.l.), though higher pressures could be reached at the expense of flow rates.
Although multiple ASAs can be used in series
for sampling by using the bypass position of the
solenoid valves, we have chosen a parallel setup
utilizing a flow split with poppet check valves (SS6CA-MM-3, Swagelok, USA) to prevent any backflow from ASAs with inactive pumps or from the
open connections after removal of one ASA. The
position of the IRGA (Fig. 1) parallel to the ASA
has shown no discernible different results. As an
advantage over a sequential setup our parallel version allows to continue the concentration measurements of the sample gas even if the ASAs are disconnected or inactive. The IRGA can alternatively
be positioned directly before the ASA to directly
analyze the gas that subsequently flows through the
sample containers of the ASA.
The inlet selection unit and ASAs are configured and operated by a field computer via RS232 serial communication lines connected to digital controllers (C-Control I STATION 2.0, Conrad Electronics GmbH, Germany), programmed to
operate the rotation valves, solenoid valve, pump,
and digital flow meter, and to provide status information for later use in post-processing of CO2 concentration and stable isotope data. The keypad and
LCD display of the digital controllers are used to
confirm correct operation of the devices before and
during field deployment. The serial communication, data storage and post processing are handled
by scripts written in Perl language.
After having completed an in situ field sampling sequence, the ASAs with up to 33 or 44 gas
sample containers per ASA are transported back to
208
the laboratory for subsequent (same day) isotope
ratio analysis.
209
Laboratory setup
207
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
3
The precise determination of δ 13 C and δ 18 O values in CO2 of large numbers of air samples implies a precise and reproducible sampling technique as well as an automated and easy-to-use
coupling of the sample containers (glass flasks or
steel loops) to the Isotope Ratio Mass Spectrometer (Delta plus XP, Finnigan MAT, Bremen, Germany).
A series of multiposition valves are used for
the flow path of the sample preparation (Fig.
3).
A 6-position dead-end path Valco-valve
(ASD6MWE,VICI, Schenkon, Switzerland) and a
4-port 2-position Valco-valve (AC4UWE, VICI,
Schenkon, Switzerland) allow the alignment of up
to four independent reference air gas bottles (laboratory air gas cylinder with different CO2 mixing ratios and δ -values) or helium, using the same
sample preparation path as the gas sampled with
the ASA allowing referencing according to the
Identical Treatment (IT) principle. 21 A feed capillary delivers pure He to the ASA (Fig. 3, valves
1 and 2), allowing a pressure build-up in the glass
flasks that flushes the sample gas at a rate of about
5 mL min−1 through a water trap (Nafion dryer) to
the cryogenic focus trap where condensable gases
(mainly CO2 and N2 O) are cryogenically trapped.
After diverting the non-condensable gases to a vent
(Fig. 3, valve 4), the cryogenically trapped sample
is thawed and subsequently flushed by He into the
Gas Chromatograph column (Poraplot Q 25 m ×
320 nm i.d., Varian, Walnut Creek, USA, held at
24 ◦ C) to allow separation of CO2 from N2 O and is
subsequently led to the Isotope Ratio Mass Spectrometer for analysis (Fig. 3, valve 5). The trapping efficiency was checked beforehand with an
IRGA (LI-840, LI-COR, Lincoln, Nebraska, USA)
behind the frozen cryogenic trap. In contrast to
Theis et al. 19 , who used a Precon (Finnigan MAT)
hooked up to the Isotope Ratio Mass Spectrometer, we modified the Gasbench II system (Finnigan
MAT) to directly interface with individual ASA
units. This modification of the Gasbench (Fig. 3,
bottom panel) comprises the replacement of the
“Gas Chromatograph”-type split 22 by a ConFloIIIlike split 23 and the replacement of the stainless
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
steel sample loop with a home-built cryogenic focus trap (1/16" stainless steel capillary filled with
Ni-wire) at the 8-port valve inside the Gasbench,
which is configured to operate as 6-port valve (Fig.
3, valve 4). A second 4-port 2-position Valcovalve (AC4UWE, VICI, Schenkon, Switzerland)
inside the sample preparation path (Fig. 3, valve
3) operates as a vent to release the pressure excess inside the sample containers and allows for
high flow purging of the sample preparation path
(10 mL min−1 ) and the Isotope Ratio Mass Spectrometer flow path (17 mL min−1 ) with pure He.
In our system without Precon this would otherwise
not have been possible. Without the posibility to
flush with high flow (50 mL min−1 ) as shown by
Theis et al. 19 , our measurement time would have
been 835 s. With the help of the pressure vent and
related high He flows we are able to reduce the
analysis time per sample to 610 s, a period comparable to Theis et al. 19 .
The cryogenic trap and all valves in the Gasbench, the external referencing unit, the rotary
valve systems of the ASA and an automated liquid
nitrogen refill procedure are computer controlled
by modified Isodat script language (ISL) scripts,
available in the vendor supplied ISODAT NT software package (Ver. 2.0 SP2.63, Finnigan MAT).
To avoid overloading of the cryogenic trap
with sample gas of high CO2 concentration (>
1000 µ mol mol−1 ) and to circumvent a possible
non-linearity of the Gasbench and Isotope Ratio Mass Spectrometer combination with signal
strength a , the signal strength of each sample is adjusted to be close to that of the Isotope Ratio Mass
Spectrometer reference by changing the cryogenic
trapping period depending on the sample concentration. We first tested the relation between the
sample CO2 concentration and the cryogenic trapping period empirically for each of the different
sample container volumes and tube lengths, determined the best fit (Fig. 4) and tested the results
with known dilutions of a CO2 in air mixture of
a known stable isotope composition. Furthermore,
to improve stable conditions for the cryogenic trap,
the liquid nitrogen (LN2 ) level in the Dewar was
kept within the 95–100% range, either by manual
refill or automated refill. To facilitate partly unattended operation (12 hours) and thus a certain level
of autonomy of this setup, we installed a LN2 rea The effect should be < 0.06‡V −1
337
fill system that consists of a balance measuring the
weight loss of the evaporating LN2 from the Dewar
in combination with timing signals received from
the Isotope Ratio Mass Spectrometer (Fig. 5) and
that is supplied by a 30 L LN2 tank (up to 48 hours
operation). Empirically, de-icing of the Dewar is
required every 12 hours.
As a last step, the ISODAT NT software configuration had to be adjusted to our modified setup, in
particular the measurement timing schedule (Fig.
6). First, the sample preparation steps of flushing the capillaries with He and sample gas through
the input lines before the gasbench, which is conventionally done between two measurements using a “pre-script”, is scheduled during and in parallel with the IRMS analysis for the next measurement. A second important modification that helped
to save time was achieved by switching to high He
flow rates while purging the input line capillaries
before and in the Gasbench as described above.
Third, changes to the ISODAT NT software configuration for the Gasbench allowed for variably
timed operations parallel to the measurement of
the reference standards (multitasking) within the
“chromatography” part of the measurement time
schedule. Thus, the cryogenic trapping period
could be varied within the chromatogram sequence
without disturbing other tasks (e.g. the measurement of the reference standards) and was no longer
required to be executed before the chromatogram
(e.g. in a pre-script). The combination of the described modifications allowed to shorten the IRMS
measurement time per sample and increased the
number of samples analyzed per day.
338
Isotope ratio analysis
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
The carbon and oxygen isotopic composition of
the CO2 is expressed as the relative difference of
its isotope abundance ratio relative to that of an international standard. This difference, usually expressed in per mill, is defined as
¸
(13 C/12 C)Sample
− 1 · 103
δ C[‡]V–PDB = 13 12
( C/ C)V–PDB
·
13
·
δ 18 O[‡]V–PDB–CO2 =
(1)
¸
(18 O/16 O)Sample
−
1
· 103
(18 O/16 O)V–PDB–CO2
(2)
for δ 13 C for the reference standards, according to the vendor supplied instruction manual.
4
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
Post-run off-line calculation and drift correction for assigning the final δ 13 C and δ 18 O values on the V-PDB (Vienna PeeDee Belemnite) and
V-PDB-CO2 scaleb were done following the IT
principle as described by Werner and Brand 21 .
The δ 13 C and δ 18 O values of the laboratory air
standards (Zurich CO2 -in-air standards) were determined at the Max-Planck-Institut für Biogeochemie (MPI-BGC, Jena, Germany) according to
Werner et al. 25 . The accurate assignment of the
corresponding δ -values on the V-PDB and the VPDB-CO2 scale was performed in Jena by measuring the Zurich CO2 -in-air standards versus the
“Jena-Reference AirSet” (J-RAS) as standard reference material (SRM).e.g. 24 Any isotope ratio
data presented in this article are reported in [‡]
deviation from V–PDB and V–PDB–CO2 for 13 C
and 18 O, respectively. Typically several measurements of a laboratory reference standard are placed
at the beginning and at the end of each measurement series, for post-calculation of corrections.
Quality control (QC) standards are used to evaluate this correction procedure.
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
Results and discussion
After ensuring linearity, we tested the effects of the
variable cryogenic trapping period of our ASA–
Gasbench–Isotope Ratio Mass Spectrometer setup
on δ 13 C measurements for a range of CO2 concentrations and for different sample containers used
(glass or metal). Furthermore, we tested the performance (precision, accuracy) of the δ 13 C measurements for typical use of the described ASA–
Gasbench–Isotope Ratio Mass Spectrometer setup.
Linearity tests with gases of different CO2 in
air or He mixing ratios have shown a strong relationship between the IRMS peak amplitude and
the offset between the δ 13 C (or δ 18 O) of CO2 in
a sample and its δ 13 C (or δ 18 O) reference value
(Fig. 7). For δ 13 C, this offset increases strongly
with lower relative peak amplitude. We suppose
the origin of this effect is the signal to noise ratio
of the analysis. Thus, to ensure measurement intercomparability, it is required to correct for this effect, e.g. by optimizing the peak amplitudes of the
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
b The
samples to a limited range close to the amplitudes
of the Isotope Ratio Mass Spectrometer reference
gas. This optimization in effect means that the
cryogenic trap should freeze the same amount of
CO2 for each sample, independent of sample container and capillary volumes. Due to differences
in pressure build-up as function of container volume, the relationships between CO2 concentration
of the sample and the trapping period required for
a peak amplitude close to the reference have to be
determined empirically (cf. Fig. 4, Table 1) and
were thus tested by analyzing a broad range of dilutions of a CO2 in air mixture with CO2 free air
(Fig. 8, top panel). The resulting relative amplitudes for this range of diluted samples (Fig. 8, bottom panel) are between 85 and 125%, well within
the typical variability of peak amplitudes (cf. Fig.
7), reflecting the quality of the chosen fit function
and the inaccuracy caused by the low time resolution of the variable trapping period (Fig. 4).
This last aspect is mostly defined by the 1 s time
resolution of the Isotope Ratio Mass Spectrometer chromatogram procedure, for which the inaccuracy increases at higher CO2 concentrations. For
example, CO2 delivered by steel capillary for the
concentration range [355,390] µ mol mol−1 and
[1365,1502] µ mol mol−1 are represented by a 34 s
and 20 s trapping period, respectively. If very
high concentrations (> 5000 µ mol mol−1 ) are expected, the relative peak amplitude of the samples
could be allowed to be > 100%. However, a new
empirical relation would need to be determined
for lower flow rates of sample through the cryogenic trap or the Isotope Ratio Mass Spectrometer
software for the variable trapping period (see Appendix) would need to be changed to use a time
resolution shorter than 1 s. In any case, application of the empirical relations of trapping period
and sample concentration requires not only that the
concentration needs to be known prior to IRMS
analysis, but also that the CO2 concentration data
from the IRGA (Fig. 1) needs to be collected and
processed prior to the laboratory analysis.
Since we modified the Isotope Ratio Mass
Spectrometer setup substantially, we tested the performance (i.e. precision and accuracy) by mea-
virtual non-existing standard V-PDB is defined by adopting a δ 13 C value of +1.95 ‡ and a δ 18 O value of –2.2 ‡ for
NBS 19 exactly. Via assigning these δ -values the hypothetical mineral V-PDB or rather the CO2 produced from it would be the
standard for δ 13 C and δ 18 O values. The term V-PDB-CO2 refers to the oxygen isotopic composition of the CO2 evolved from
the mineral by reaction with water-free H3 PO4 at 298 K. For details, see e.g. Ghosh et al. 24
5
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
suring δ 13 C (and δ 18 O) of a laboratory reference
standard and QC standards that passed through the
sample flow path (Fig. 9) or were sampled by
the ASA beforehand (Fig. 10). The overall precision of δ 13 C measurements was determined to
be <0.08‡ (σ ) for samples with standards stored
in glass flasks inside an ASA (N=33), <0.11‡
(σ ) for samples with standards stored in stainless
steel loops inside an ASA (N=44) and <0.06‡
(σ ) for directly supplied standards (N=5), over the
course of several measurement campaigns between
February 2006 and March 2008. The decrease in
precision with increasing sample numbers (N=5,33
or 44) suggests that reference standards must be included in the sample sequence more frequently to
correct for possible drift effects. The slight difference between the QC standard I and II (Fig. 9) can
be explained by methods to determine the respective reference value. For the QC standard I the reference value was determined by the ETH IsoLab
based on an average difference (N=5) to the laboratory reference standard. For the second QC standard on the other hand, the reference value was determined by an internationally acknowledged laboratory against several international standards with
high precision. In general, based on periodic measurements of standards (mostly QC Standard I) using the ASAs, the overall accuracy was determined
to be 0.11±0.04‡ (σ ), reflecting measurements
with the ASA–Isotope Ratio Mass Spectrometer
setup during one year, i.e. March 2007 to March
2008. For δ 13 C, we did not find an effect of the
surface properties (e.g. volume, surface:volume,
surface material) of the stainless steel loop versus the glass flask sample containers on the precision and accuracy of stored samples. However,
for δ 18 O, the used stainless steel loop containers appeared inadequate and would require extensive pre-treatment, such as the removal of residual water from the surfaces that can otherwise exchange oxygen atoms in an equilibrium reaction
with CO2 and thus potentially change the stable
isotope composition of the sample. A treatment
with long periods of dry air flushing in combination with heating, as suggested by Gemery et al. 16 ,
makes steel loops far less practical for δ 18 O measurements than their counterpart, i.e. glass flask
as sample containers. We evaluated the reliability
of the filling procedure of the ASAs and the influence of transport of samples from the field to the
504
laboratory by filling the same ASA in the field and
sebsequently in the laboratory with the same standard gas. The resulting δ 13 C and δ 18 O measurements showed no significant difference (∆δ 13 C=0.04‡, ∆δ 18 O=0.05‡, N=5) between the respective filling locations (Sophia Etzold, Institute of
Plant Sciences, ETH Zurich, Switzerland, unpublished data).
For studies using the Keeling plot approach,
e.g. to determine the signature of the respiration
source via a statistical regression approach, the
optimization of peak amplitudes provides a clear
and essential improvement for intercomparability
of δ 13 C measurements. 8 Small (systematic) errors
in δ 13 C values would lead to much larger uncertainty in the determination of the respiration signature (the intercept of the Keeling plot regression line). 4,11 Our results show that the system described here not only can provide precision of at
least 0.1‡ with an accuracy of 0.11±0.04‡ (σ )
for δ 13 C, but also allows unattended operation in
the field and retain a measurement time per sample of 610 s. This clearly fullfills the quality criteria necessary to perform gradient measurements of
stable isotope ratios of CO2 in air for the study of
atmosphere–biosphere interactions.
505
Acknowledgments
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
515
Peter Plüss (ETH) and Patrick Flütsch (ETH) are
kindly acknowledged for their extensive technical support. We would like to thank Matthias
Saurer (PSI), Willi A. Brand (MPI-BGC), Michael
Rothe (MPI-BGC) and Sophia Etzold (ETH) for
their advice and helpful discussions. Our work has
also benefited from discussions with Peter Weigel
and Andreas Hilkert (Thermo Fischer). This work
has been supported by the Swiss National Science
Foundation (SNF), grant 200021-105949.
516
References
506
507
508
509
510
511
512
513
514
517
518
519
520
521
522
6
1. IPCC. Climate Change 2007: The Physical
Science Basis. Contribution of Working Group
I Contribution to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press
2007. ISBN 0521705967.
523
524
2. Yakir D, Wang XF. Nature 1996; 380: 515–
517.
564
565
566
525
526
3. Bowling DR, Tans PP, Monson RK. Global
Change Biology 2001; 7: 127–145.
567
568
527
528
529
530
531
4. Pataki DE, Ehleringer JR, Flanagan LB,
Yakir D, Bowling DR, Still CJ, Buchmann
N, Kaplan JO, Berry JA.
Global Biogeochem. Cycles 2003; 17: 1022. DOI:
10.1029/2001GB001850.
569
570
571
572
573
532
533
534
535
536
5. Ogee J, Peylin P, Ciais P, Bariac T, Brunet
Y, Berbigier P, Roche C, Richard P, Bardoux G, Bonnefond JM.
Global Biogeochem. Cycles 2003; 17: 1070. DOI:
10.1029/2002GB001995.
574
575
576
577
578
537
538
6. Knohl A, Buchmann N. Global Biogeochem.
Cycles 2005; 19: GB4008.
579
580
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
7. Bowling DR, Pataki DE, Randerson JT. New
Phytologist 2008; 178: 24–40.
DOI:
10.1111/j.1469-8137.2007.02342.x.
581
8. Keeling CD. Geochim. Cosmochim. Acta
1958; 13: 322–334.
584
9. Keeling CD. Geochim. Cosmochim. Acta
1961; 24: 277–298.
586
10. Ogee J, Peylin P, Cuntz M, Bariac T, Brunet
Y, Berbigier P, Richard P, Ciais P. Global Biogeochem. Cycles 2004; 18: GB2019. DOI:
10.1029/2003GB002166.
588
11. Zobitz JM, Keener JP, Schnyder H, Bowling
DR. Agric. For. Meteorol. 2006; 136: 56–75.
12. Tuzson B, Zeeman MJ, Zahniser MS,
Emmenegger L.
Infrared Physics &
Technology 2008; 51 : 198–206. DOI:
10.1016/j.infrared.2007.05.006.
582
583
585
587
589
590
591
592
593
594
595
596
597
598
556
557
558
559
560
561
562
563
13. Mohn J, Zeeman MJ, Werner RA, Eugster W,
Emmenegger L. Isot. Environ. Health Stud.
2008; (in press).
14. Tuzson B, Mohn J, Zeeman MJ, Werner RA,
Eugster W, Zahniser MS, Nelson DD, McManus JB, Emmenegger L. Applied Physics B.
Lasers and Optics 2008; 92 : 451–458. DOI:
10.1007/s00340-008-3085-4.
7
15. Rothe M, Jordan A, Brand WA. In: World
Meteorological Organization Global Watch
World Meteorological Organization, 2005;
161: 64–70.
16. Gemery PA, Trolier M, White JWC. J. Geophys. Res.-Atmospheres 1996; 101: 14415–
14420.
17. Sturm P, Leuenberger M, Sirignano C, Neubert REM, Meijer HAJ, Langenfelds R, Brand
WA, Tohjima Y. Journal Of Geophysical
Research-Atmospheres 2004; 109: D04309.
18. Knohl A, Werner RA, Geilmann H, Brand
WA. Rapid Communications In Mass Spectrometrys 2004; 18: 1663–1665.
DOI:
10.1002/rcm.1528.
19. Theis DE, Saurer M, Blum H, Frossard
E, Siegwolf RTW. Rapid Commun. Mass
Spectrom. 2004; 18: 2106–2112.
DOI:
10.1002/rcm.1596.
20. Clark MJR, Whitfield PH. Water Resources
Bulletin 1994; 30: 1063–1079.
21. Werner RA, Brand WA. Rapid Commun.
Mass Spectrom. 2001; 15: 501–519. DOI:
10.1002/rcm.258.
22. Merritt DA, Brand WA, Hayes JM. Org.
Geochem. 1994; 21: 573–583.
DOI:
doi:10.1016/0146-6380(94)90003-5.
23. Werner RA, Bruch BA, Brand WA. Rapid
Commun. Mass Spectrom. 1999; 13: 1237–
1241.
24. Ghosh P, Patecki M, Rothe M, Brand WA.
Rapid Commun. Mass Spectrom. 2005; 19:
1097–1119.
25. Werner RA, Rothe M, Brand WA. Rapid Commun. Mass Spectrom. 2001; 15: 2152–2167.
599
Appendix
669
vice. The execution of the script code (or Actionscript device) within the acquisition method was
scheduled each second during a specific time window as shown in Figure 6. Contrary to the ISL
delay command for delayed operations, the proposed solution does not interfere with the timing
of other tasks during the acquisition and proved
to be a reliable and effective way of performing
time variable tasks parallel to tasks with fixed timing during the IRMS chromatogram part of a measurement. Figure 4 shows different regression fits.
Based on this, we have used different fitting functions for different concentration ranges, or applied
a look-up-table approach using if statements. We
were not able to program the power function fits
(y = a · xb ) with decimal values of “b” in the ISL
script, and have relied on Taylor or logarithmic
functions instead.
670
FIGURE CAPTIONS
652
653
600
601
602
The ISL script code used for multitasking the concentration dependend activation of the cryogenic
trap is described in the following example.
603
1
604
2
605
3
606
4
607
5
608
6
609
7
610
8
611
9
612
10
613
11
614
12
615
13
616
14
617
618
15
619
16
620
17
621
622
18
623
624
19
625
20
626
21
627
22
628
23
629
24
630
25
631
632
633
634
635
636
637
638
639
640
641
1
643
2
644
3
655
656
657
658
include " lib \ s t d i s l . i s l ";
include " lib \ Instrument . i s l ";
i n c l u d e " l i b \ GasBench_lib . i s l " ;
f u n c t i o n T r a p T i m e rF u n ( number A)
{
number B = ( −10.393 * l o g (A) ) −96;
r e t u r n B;
}
main ( )
{
number nA = _GetSequenceNumber ( "
Concentration " ,60) ;
number nB = c a l l T r a p T i m e r F u n ( nA ) ;
number nC = 150 − nB ;
number nD = _ R e f G e t P r o f i l e N u m b e r ( " ASA
" ," Start " ,0) ;
number nE = a b s ( _ G e t T i c k C o u n t ( ) − nD )
;
659
660
661
662
663
664
665
666
667
668
671
672
i f ( nE > ( nC * 1 0 0 0 ) )
{
_ S e t ( " Gas Bench / V a l c o " ,LOAD) ;
_ U s e r I n f o ( " CryoTrap a c t i v e ! " , 0 , 0 ) ;
}
}
The sample concentration is read from the sequence table and converted to a trapping period via
an empirically fitted function (code line 14–15) as
shown in Figure 4, from which a target start time
in seconds is calculated (16). The elapsed time is
calculated (17–18) and compared to the target start
time in order to decide if the trap should be set to
an activated state or not (20–24). For correct calculation of the elapsed time, the start time of the
chromatogram process was stored from the internal millisecond counter with the command code
642
645
s c r i p t TrapTimer
654
numbers nF = ( _ G e t T i c k C o u n t ( ) ) ;
_ R e g S e t P r o f i l e N u m b e r ( "ASA" , " S t a r t " ,
nF ) ;
c a l l Startchromatogram () ;
673
674
675
676
677
678
679
680
681
682
683
684
685
686
687
688
689
690
691
692
646
647
648
649
650
651
within the Acquisition ISL script used for this
method. Please note that the included lines (1–2)
are added just before the chromatogram is started
(3). For effective use of the script in the ISODAT
NT acquisition software, it was incorporated into
the Gasbench configuration as an ActionScript de-
693
694
695
696
697
8
Figure 1: Overview of improved setup, from sampling air in the field (top) to measurement by Isotope Ratio Mass Spectrometer (bottom). Communication connections and sample gas flow paths
are indicated by broken lines and thick lines, respectively. After field operation, the ASA is transported to the lab and interfaced with the Isotope
Ratio Mass Spectrometer.
Figure 2: Flow diagram of the ASA showing the
difference between field (top) and laboratory (bottom) operation. The ASA is shown in field sampling mode: the flow is diverted by the solenoid
valve, the air sample is dried, filtered and pushed
through the Valvo-valve (shown here in bypass
loop position). During sampling, an adjustable
flow regulator (set to ≈ 0.9 L min−1 ) and a poppet check valve (one-way, opening at >7 kPa) help
create a pressure excess in the glass flask or stainless steel loop sample containers. Per ASA, three
or four Valvo-valves with sample containers are
connected in series, adding up to a maximum total
of 33 or 44 samples per unit. Two manual threeway valves are used to switch between field and
laboratory setup.
Figure 3: Flow diagram of the laboratory setup.
Shown here is the situation for flow of He (valve 1)
with sample air from the ASA (2) to the Gasbench
698
699
700
701
702
703
704
705
706
707
708
709
710
711
(3) and subsequent cryogenic focus trap (4), while
at the same time the Gas Chromatograph and the
inlet of the Isotope Ratio Mass Spectrometer are
flushed with He (4 and 5). See text for details.
Figure 4: Empirical relations between sample CO2
concentration and trapping periods required for
peak amplitudes that are equal to the Isotope Ratio Mass Spectrometer reference gas, for samples
delivered to the Isotope Ratio Mass Spectrometer from three different types of containers (glass
flasks, steel loops, steel capillary). For glass flask
sample containers, two fit functions are shown. For
fit parameters and further details, see Table 1 and
Appendix.
738
739
740
741
742
743
744
745
746
747
748
749
750
712
713
714
715
716
717
718
719
720
721
722
723
724
725
726
727
728
729
730
731
732
733
734
Figure 5: Decision diagram for the automated liquid nitrogen (LN2 ) refilling system used for the
cryogenic trap. Activation of the solenoid valve for
LN2 flow into the Dewar depends on fulfillment of
the conditions for the weight of the cryogenic trap
Dewar (A), the temperature of the balance (B) and
a signal from the Isotope Ratio Mass Spectrometer
during a specific period of the IRMS measurement
protocol (C) and a waiting period after filling.
Figure 6: The timeline of the Isotope Ratio Mass
Spectrometer measurement protocol implemented
in the ISODAT NT software. The flow path of the
input line and Gasbench is flushed with sample air
(S) and the cryogenic trap is lowered into liquid
nitrogen before sample air is let into the trap to be
frozen (FS) for a period that is variable and derived
from the sample CO2 mixing ratio. After the trap
is raised to thaw, the cryogenically focused content
is carried by He through the Gas Chromatograph to
the Isotope Ratio Mass Spectrometer for analysis.
Meanwhile, the sample inlet tubes are flushed with
pure He (He) or the next sample (Snext ) with higher
flow rate (+).
751
752
753
754
755
756
757
758
759
760
761
762
763
764
765
766
767
768
769
770
771
772
735
736
737
δ 13 C
Figure 7: Linearity performance of
analysis
using the modified Gasbench, expressed as the deviation from the δ 13 C reference value against the
773
774
775
9
relative peak amplitude (A) in the chromatogram.
See text for details.
Figure 8: Application of concentration-dependent
variable cryogenic trapping periods in the Gasbench for measurements of δ 13 C. In the top panel,
the deviation from the δ 13 C reference value is
shown for different dilutions of a CO2 in air mixture with a constant δ 13 C value. In the bottom
panel, the deviation from the δ 13 C reference value
is shown for the corresponding relative peak amplitude in the chromatogram. The SD for the δ 13 C
measurements is 0.04‡ (N=13).
Figure 9: Deviation between measured δ 13 C
(δSample ) and reference δ 13 C (δRef ) for a laboratory
reference standard and two quality control (QC)
standards that were directly suplied through steel
capillaries, at different dates. The deviations of QC
standard I (top) and QC standard II (bottom) are on
average –0.02±0.04‡ and 0.06±0.05‡, respectively. The maximum observed SD for each fivesample series of reference standard and QC standards (I and II) is 0.05.
Figure 10: The deviation between measured δ 13 C
(δSample ) and reference δ 13 C (δRef ) for a laboratory
reference standard and a quality control (QC) standard that was sampled beforehand in glass flasks
(3 min of ≈ 1 L min−1 flushing into an ASA).
The maximum observed SD for each five-sample
series of reference standard is 0.05 and 0.07 for
δ 13 C and δ 18 O, respectively. For QC standard I,
the average deviations from their reference value
are 0.08±0.04‡ and –0.19±0.05‡ for δ 13 C and
δ 18 O, respectively. The QC standard I is the same
as shown in the top panel of Figure 9.
Table 1: Fit parameters for the relationships between sample CO2 concentrations and trapping periods for different types of sample containers. See
text and Figure 4 for details.
776
FIGURES AND TABLES
create a pressure excess in the glass flask or stainless steel loop sample containers. Per ASA, three
or four Valvo-valves with sample containers are
connected in series, adding up to a maximum total
of 33 or 44 samples per unit. Two manual threeway valves are used to switch between field and
laboratory setup.
Field setup
Air inlet
selection
unit
Pump
COMcontroller
0.9 L min
Particle
filter
-1
sample
Sample
sample
manifold
manifold
manifold
(ASA)
0.9 L min-1
Gas
analyzer
COMcontroller
Field PC
Transport to the lab
Lab setup
Hesample
& Ref.
manifold
valve
COMcontroller
Gasbench
Sample
sample
sample
manifold
manifold
manifold
(ASA)
COMcontroller
Cryogenic
focus trap
LN2 dewar
COMcontroller
777
Reference and sample preparation
Mass
Spectrometer
He
COMcontroller
He
Vent
Vent
4
5
He
(Dilution off)
Cryogenic
focus trap
Split
Mass
Spectrometer
Figure 3: Flow diagram of the laboratory setup.
Shown here is the situation for flow of He (valve 1)
with sample air from the ASA (2) to the Gasbench
(3) and subsequent cryogenic focus trap (4), while
at the same time the Gas Chromatograph and the
inlet of the Isotope Ratio Mass Spectrometer are
flushed with He (4 and 5). See text for details.
Adjustable
flow meter
Poppet
check
valve
100
●
●
Digital
flow
meter
Entrapment period [s]
Field
Gas
Chromatograph
Water trap
779
Lab
Particle
filter
12-pos. Valco-valve
with 11 sample volumes
He, high flow
He
Pump
Drying
column
Water trap
A
3
He
+
Sample
Sample
manifold
(ASA)
Gasbench II, modified
Out
Solenoid valve
He
Lab PC
A
Vent
2
1
Ref 1
Figure 1: Overview of improved setup, from sampling air in the field (top) to measurement by Isotope Ratio Mass Spectrometer (bottom). Communication connections and sample gas flow paths
are indicated by broken lines and thick lines, respectively. After field operation, the ASA is transported to the lab and interfaced with the Isotope
Ratio Mass Spectrometer.
Sample in
Ref 2
Ref 3
●
80
●
60
●
Glass flasks (ASA); y = a1·x1+a2·x2+a3·x3+b
Glass flasks (ASA), alt. fit; y = a·xb
Steel loops (ASA); y = a·ln(x)+b
Steel capillary (Ref. inlet); y = a·ln(x)+b
●
●
●
40
●
● ●
●
●
●
●
●
40
●
●
20
20
0
300
778
Sample + He
to GasBenchMass Spectrometer
780
80
60
●
●
0
He in
100
500
700
900
1100
1300
1500
CO2 concentration [µ
µmol mol−1]
Figure 4: Empirical relations between sample CO2
concentration and trapping periods required for
peak amplitudes that are equal to the Isotope Ratio Mass Spectrometer reference gas, for samples
delivered to the Isotope Ratio Mass Spectrometer from three different types of containers (glass
flasks, steel loops, steel capillary). For glass flask
sample containers, two fit functions are shown. For
fit parameters and further details, see Table 1 and
Appendix.
Figure 2: Flow diagram of the ASA showing the
difference between field (top) and laboratory (bottom) operation. The ASA is shown in field sampling mode: the flow is diverted by the solenoid
valve, the air sample is dried, filtered and pushed
through the Valvo-valve (shown here in bypass
loop position). During sampling, an adjustable
flow regulator (set to ≈ 0.9 L min−1 ) and a poppet check valve (one-way, opening at >7 kPa) help
10
Dewar for the
cryogenic trap
A) Balance
781
m < "tare"
B) Temperature
of the balance
T > -20°C
C) IRMS
Signal during
acquisition
Solenoid
COMController valve
LN2
Figure 5: Decision diagram for the automated liquid nitrogen (LN2 ) refilling system used for the
cryogenic trap. Activation of the solenoid valve for
LN2 flow into the Dewar depends on fulfillment of
the conditions for the weight of the cryogenic trap
Dewar (A), the temperature of the balance (B) and
a signal from the Isotope Ratio Mass Spectrometer
during a specific period of the IRMS measurement
protocol (C) and a waiting period after filling.
782
Figure 6: The timeline of the Isotope Ratio Mass
Spectrometer measurement protocol implemented
in the ISODAT NT software. The flow path of the
input line and Gasbench is flushed with sample air
(S) and the cryogenic trap is lowered into liquid
nitrogen before sample air is let into the trap to be
frozen (FS) for a period that is variable and derived
from the sample CO2 mixing ratio. After the trap
is raised to thaw, the cryogenically focused content
is carried by He through the Gas Chromatograph to
the Isotope Ratio Mass Spectrometer for analysis.
Meanwhile, the sample inlet tubes are flushed with
pure He (He) or the next sample (Snext ) with higher
flow rate (+).
11
(ASample / ARef) × 100 [%]
0
50
100
200
400
02:00
O
0.4
δSample − δRef [‰]
0.2
0.2
●
●●
●●
●
●
●
●● ● ● ●
●
●
●
● ●
●
● ● ●
●
●● ●
●
●●
●●
● CO2 in air (400 µmol mol−1)
●
● ●
●●
CO2 in He (4000 µmol mol−1)
0.0
−0.2
−0.4
13
0.4
C
0.2
0.0
δSample − δRef [‰]
18
0.4
0.0
−0.2
−0.4
−1
●
●
●●●
● ●
● ●●●●
●● ●● ●
●
●● ●●
●●●●
● ●●
●● ●
● ●
● ●●●
● CO2 in air (400 µmol mol )
CO2 in He (4000 µmol mol−1)
0.4
0.2
0.2
−0.2
●●●
●●
0
50
200
Figure 7: Linearity performance of δ 13 C analysis
using the modified Gasbench, expressed as the deviation from the δ 13 C reference value against the
relative peak amplitude (A) in the chromatogram.
See text for details.
C
●●
●
●●
δSample − δRef [‰]
−1
CO2 concentration [µ
µmol mol ]
900
1200
1500
1800
δSample − δRef [‰]
13
C
0.2
0.0
−0.2
C
0.2
786
0.0
0
50
100
150
200
(ASample / ARef) *100 [%]
Figure 8: Application of concentration-dependent
variable cryogenic trapping periods in the Gasbench for measurements of δ 13 C. In the top panel,
the deviation from the δ 13 C reference value is
shown for different dilutions of a CO2 in air mixture with a constant δ 13 C value. In the bottom
panel, the deviation from the δ 13 C reference value
is shown for the corresponding relative peak amplitude in the chromatogram. The SD for the δ 13 C
measurements is 0.04‡ (N=13).
●
●●●●
00:00
●●●●
●
●
●●●
●
●●●
●●
Reference standard
04:00
−0.2
0.2
0.0
−0.2
08:00
18:00
20:00
22:00
00:00
C
0.4
0.2
●
●
●
●●●
●
●● ●●●●●●●● ●●●●● ●●●●● ●●●●●
●
0.0
−0.2
−0.4
0.4
0.2
0.0
−0.2
2008−03−12
● QC standard I
Reference standard
18
● QC standard I
Reference standard
O
−0.4
0.4
0.2
0.0
●
●● ●●
●
●
●
● ●
● ●● ●●●●● ●● ●●●●●● ● ●●● ●●
●
−0.2
2008−03−12
−0.4
18:00
20:00
22:00
00:00
Time of day [h]
Figure 10: The deviation between measured δ 13 C
(δSample ) and reference δ 13 C (δRef ) for a laboratory
reference standard and a quality control (QC) standard that was sampled beforehand in glass flasks
(3 min of ≈ 1 L min−1 flushing into an ASA).
The maximum observed SD for each five-sample
series of reference standard is 0.05 and 0.07 for
δ 13 C and δ 18 O, respectively. For QC standard I,
the average deviations from their reference value
are 0.08±0.04‡ and –0.19±0.05‡ for δ 13 C and
δ 18 O, respectively. The QC standard I is the same
as shown in the top panel of Figure 9.
−0.2
2007−07−18
●
●●●●
● QC standard II
20:00
16:00
0.0
Reference standard
13
0.0
−0.4
13
0.2
0.2
−0.2
−0.2
2007−07−18
−0.2
784
0.2
0.0
●●●
● ●
●●
●●●
●●●●
●
2008−03−13
16:00
600
● QC standard I
Time of day [h]
0.4
300
0.0
Figure 9: Deviation between measured δ 13 C
(δSample ) and reference δ 13 C (δRef ) for a laboratory
reference standard and two quality control (QC)
standards that were directly suplied through steel
capillaries, at different dates. The deviations of QC
standard I (top) and QC standard II (bottom) are on
average –0.02±0.04‡ and 0.06±0.05‡, respectively. The maximum observed SD for each fivesample series of reference standard and QC standards (I and II) is 0.05.
400
(ASample / ARef) × 100 [%]
0
●●●●●
13
785
100
●
●
●●●
2008−02−26
−0.2
783
18:00
0.2
●●●●
●
16:00
0.0
−0.2
14:00
C
0.0
0.2
10:00
13
0.0
−0.2
06:00
787
12
Table 1: Fit parameters for the relationships between sample CO2 concentrations and trapping periods for
different types of sample containers. See text and Figure 4 for details.
Fit function
Fit parameters
1
2
3
Glass flasks (in ASA) y = a1 · x + a2 · x + a3 · x + b a1 = −3.71 · 10−1 , a2 = 3.536 · 10−4 ,
a3 = −1.215 · 10−7 , b = 174
a = −15.37, b = 144
Steel loops (in ASA) y = a · ln(x) + b
Steel capillary (Ref. & QC standards) y = a · ln(x) + b
a = −10.39, b = 96
13