Domestic Road Infrastructure and International
Transcription
Domestic Road Infrastructure and International
Domestic Road Infrastructure and International Trade:
Evidence from Turkey
A. Kerem Co¸sar
Banu Demir
University of Chicago
Booth School of Business
Bilkent University
Department of Economics
January 2015
Abstract
Drawing on the large-scale public investment in roads undertaken in Turkey
during the 2000s, this paper contributes to our understanding of how internal
transportation infrastructure affects regional access to international markets.
Using data on international trade of Turkish provinces and the change in the
capacity of the roads connecting them to the international gateways of the
country, we estimate distance elasticity of trade associated with roads of varying
capacity in a gravity setting. Two key results emerge. First, the cost of an
average shipment over a high-capacity expressway is 65 to 75 percent lower
than it is over single-lane roads. Second, the reduction in transportation costs
is greater the more time-sensitive an industry is. To the extent that efficient
logistics enable countries to take part in global supply chains and exploit
their comparative advantages, our findings have important developmental
implications.
JEL Codes: F14, R11, R41.
Keywords: international trade, market access, transportation infrastructure,
time-sensitive industries.
Correspondence: kerem.cosar@chicagobooth.edu, banup@bilkent.edu.tr.
1
Introduction
Poor domestic transportation infrastructure in developing countries is often cited as an
important impediment for accessing international markets. Yet, evidence on how a major
improvement in the transport network of a country affects the volume and composition of
its international trade is scarce. We fill this gap by estimating the impact of a recent largescale public investment in Turkey aimed at improving the quality of the road network. Our
main finding is that, by reducing the distance elasticity of shipping costs, high-capacity
expressways improved the foreign market access of regions remote from the ports.
A typical international shipment involves both domestic and international transportation
with a possible transhipment across different modes at a harbor, an airport, or a border crossing. Quantitative models of international trade rarely distinguish these separate segments.
Bilateral distances used in the estimation of gravity equation are typically the distances
between the main cities of countries. While measures taking into account internal distances
are available (Redding and Venables 2004), they do not explicitly control for the quality
of transportation infrastructure which is clearly important in determining domestic freight
costs besides distance.
Intuition and evidence suggest that the domestic component may account for a nonnegligible part of the overall cost of shipping goods across borders. Decomposing the ad valorem
tax equivalent of trade costs between industrialized countries, Anderson and van Wincoop
(2004) estimate that domestic distribution costs are more than twice as high as international transportation costs (55 versus 21 percent, respectively). Rousslang and To (1993)
document that domestic freight costs on US imports are in the same order of magnitude as
international freight costs. Using data on the cost of shipping a standard container from
Baltimore to 64 destination cities around the world, Limao and Venables (2001) find that
the per unit distance cost in the overland segment of the journey is significantly higher than
in the sea leg. Moreover, these costs critically depend on the quality of the transportation infrastructure. Atkin and Donaldson (2014) estimate that intranational trade costs in
1
Ethiopia and Nigeria are 4 to 5 times larger than the estimates obtained for the United
States. Consistent with this evidence, recent policy initiatives emphasize that an inadequate
transportation infrastructure and inefficient logistics sector can severely impede developing
countries’ competitiveness (WTO 2004; WB 2009; ADBI 2009). For instance, the World
Bank cites trade facilitation, which incorporates domestic transportation, as its “largest and
most rapidly increasing trade-related work” as of 2013. Thus, quantifying the effect of internal transportation costs on international trade and understanding its channels are important
for assessing trade-related benefits of transportation infrastructure investments.
Between 2003 and 2012, Turkey increased the share of four-lane expressways in its interprovincial road stock from 11 to 35 percent. The expansion of existing two-lane roads into
divided four-lane expressways significantly improved the quality and capacity of roads while
the total length remained essentially unchanged. Important for our study, these investments
affected regions differently depending on where they were made, improving the connectivity
of some regions to the international trade gateways of the country more than others. Exploiting this variation, we estimate that the investment under study significantly reduced
transport costs, and thus increased regional exports and imports. Our results suggest three
key drivers behind this effect: an increase in the number of countries traded, average volume of trade per country, and the number of industries traded. These results are robust
to alternative specifications and instrumenting the change in route-specific road capacity
with the initial capacity. Next, we show that transportation-intensive industries displayed
higher export growth in regions with above-average improvements in connectivity. This constitutes a plausible channel for the aggregate response of regional exports and strengthens
our identification.
Recent work highlights the prevalence and importance of the issues that we explore. As
noted above, Atkin and Donaldson (2014) estimate large internal trade costs in Ethiopia and
Nigeria. Co¸sar and Fajgelbaum (2014) develop a model in which these costs lead to regional
specialization in export-oriented industries close to ports, and verify this prediction in China.
2
Allen and Arkolakis (2014) incorporate realistic topographical features of geography into
a spatial model of trade and estimate the rate of return to the US Interstate Highway
System. Focusing on historical episodes, Donaldson (2012) and Donaldson and Hornbeck
(2013) analyze the welfare gains from railroads in India and the United States, respectively.
We complement these studies by providing evidence on how a large-scale, capacity-enhancing
public investment on transportation infrastructure in a developing country affects the volume
and composition of its regions’ international trade.
Our paper also contributes to a strand of literature that focuses on estimating the effect
of transport infrastructure on trade and sectoral productivity. Using cross-country data,
Limao and Venables (2001) and Yeaple and Golub (2007) find that infrastructure is an important determinant of trade costs, bilateral trade volumes, and comparative advantage.1
Volpe Martincus and Blyde (2013) use the 2010 Chilean earthquake as a natural experiment
to estimate the response of firm-level exports to the resulting geographical variation in access
to ports. Volpe Martincus, Carballo, and Cusolito (2013) use historical routes in Peru to
instrument for the location of new roads and find a sizeable impact on firm-level exports. A
recent report by IADB (2013) explores the importance of domestic transportation infrastructure for regional exports in a number of Latin American countries. We complement these
studies by proposing an alternative measure of road quality and an identification strategy
for estimating its effect on trade. We also explore the importance of alternative channels
through which transportation infrastructure could exert its effects. To the extent that reducing internal transport costs helps developing countries participate in global supply chains
in transportation-intensive industries, our results have important implications for industrial
and commercial policies.
The next section introduces the background and the data. The results are presented in
section 3.
1
Besides the length of roads, paved roads, and railways per sq km of country area, the infrastructure index
used by Limao and Venables (2001) contains telephone main lines per person as well, making it impossible
to tease out the isolated effect of the transportation infrastructure. In contrast, Yeaple and Golub (2007)
investigate roads, telecom, and power infrastructure separately and find roads to have the biggest effect.
3
2
Data and Preliminary Analysis
2.1
Background
Turkey is an upper-middle-income country with a large population (77 million as of 2013)
and a diversified economy. The country is the world’s 17th-largest economy, 22th-largest
exporter and 13th-largest importer of merchandise goods by value (World Trade Report
2014, excluding intra-EU28 trade). It has been in a customs union for manufactured goods
with the European Union since 1996, which accounts for more than half of the country’s
trade. Turkey is the fifth-largest exporter to the European Union and its seventh-largest
importer.
Administratively, the country is divided into 81 contiguous provinces (il in Turkish) of
varying geographic and economic size.2 Each province is further composed of districts (il¸ce).
Some of these districts jointly form the provincial center (il merkezi ), which is typically
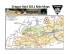
the largest concentration of urban population in a province. Figure 1 outlines provincial
boundaries and centers (see the notes to the figure).
Road transport is the primary mode of freight transport in Turkey. It accounts for about
90 percent of domestic freight (by tonne-km) and passenger traffic.3 While the interprovincial
road network has been extensive and paved, its capacity was considered quite inadequate
until recently. In order to relieve the congestion and reduce the high rate of road accidents,
the authorities launched a large-scale public investment in 2002 in order to expand existing
single carriageways (i.e., two-lane undivided roads) into dual carriageways (i.e., divided fourlane expressways). The investment was centrally planned and financed from the central
government’s budget with no direct involvement of local administrations.
As a result, the length of dual carriageways increased by more than threefold during the
2003-2012 period, while total road stock remained essentially unchanged (figure 2). This
2
Provinces correspond to the NUTS 3 (Nomenclature of Territorial Units for Statistics) level in the
Eurostat classification of regions.
3
See page 7 in GDH (2012). Data on modal shares by value are not available.
4
capacity-expansion feature of the investment distinguishes the episode under study from
the construction of new roads or the pavement of existing dirt roads, settings on which the
related literature typically focuses (IADB, 2013).
External evidence confirms that the upgrades improved road transport quality in Turkey.
Since 2007, the World Bank has been conducting a worldwide survey among logistics professionals every two years. The results are aggregated into the Logistics Performance Index
(LPI), which ranges between 0 and 5; a higher LPI value indicates a more developed transportation sector as perceived by industry experts. In 2007, Turkey’s score was 2.94, lower
than the OECD average of 3.61. In 2012, Turkey’s LPI value of 3.62 almost caught up with
the OECD average of 3.68. Broken down into its components, the LPI covers the following
six areas: customs, infrastructure, international shipments, logistics competence, tracking
and tracing, and timeliness. In 2007, Turkey ranked 39th among 150 countries for the quality of trade- and transport-related infrastructure, and 52th for the timeliness of domestic
shipments in reaching the destination. In 2012, Turkey scored higher on both indices; the
country moved up 14 places in the infrastructure ranking, and 25 places in the timeliness
ranking. Furthermore, according to the Global Competitiveness Report (World Economic
Forum) rankings based on the quality of road infrastructure, Turkey moved up 10 places to
43th among 148 countries between 2006-2012.4
We finish this subsection by noting that the objectives of the investment program alleviate
concerns related to the selection of provinces for foreign trade-related outcomes. Policy documents explicitly state that the goal was “to ensure the integrity of the national network and
address capacity constraints that lead to road traffic accidents.”(GDH 2014). The long-term
goal is to improve connections between all provincial centers to form a comprehensive grid
network spanning the country, rather than boosting exports from particular regions. Against
4
The ranking is constructed based on a survey question that asks respondents to rate the quality of roads
in their countries from 1 (“extremely underdeveloped”) to 7 (“extensive and efficient—among the best in
the world”). Turkey improved its score from 3.72 in 2006-2007 to 4.87 in 2012-2013. Demir (2011) also uses
quality indices published by the World Economic Forum and reports that the elasticity of Turkey’s trade
with respect to the quality of its overall transport infrastructure is around unity.
5
this backdrop, we will further address endogeneity concerns in our empirical investigation.
2.2
Data
Data on province-level manufacturing exports and imports for the 2003-2012 period are
provided by the Turkish Statistical Institute (TUIK). An important aspect of these flows
for our purposes is the gateway g through which trade occurs. 20 out of 81 provinces are
gateway provinces, hosting either a seaport or a border crossing (See figure 1, top panel).
We observe annual trade flows between each province-gateway pair: tradefpgt denotes export
or import flow f = {exp, imp} of province p through gateway g at year t, denominated in
current year USD.
Trade flows are further disaggregated by partner country and 24 manufacturing industries
(in 2 digit ISIC Rev.3 classification). For confidentiality reasons, TUIK does not disclose
the data at the province-gateway-country-industry (pgci) level since individual firms may
be detected at this level of detail. We thus work with trade data at the province-gateway
(pg), province-gateway-country (pgc) and province-gateway-industry (pgi) levels, depending
on the specification.
Data on the stock and composition of roads at the province level are provided by the Turkish General Directorate of Highways. To be precise, our data inform us about the total length
of intercity roads (roadStockpt ) and expressways (expresswaypt ) within provincial boundaries at each year between 2003-2012. By definition, expresswaypt ≤ roadStockpt , which
holds with strict inequality for all province-year observations. Figure 2 plots countrywide
total length of roads and expressways over time, showing that while the road stock remained
more or less stable after 2002, an increasing fraction of it was upgraded to expressways.
Several remarks are in order. The road data is available at a level of aggregation that
does not inform us about particular segments between nodes. Neither do we have geographical information about the network. Figure 3 helps to illustrate this. The three tiles here
represent three provinces, their centers and boundaries. At any given year, the network is
6
composed of single carriage roads (red lines) and expressways (black lines). We only know
the total length of these roads within provincial boundaries, rather than whether there is
an expressway connecting the centers (P1 , P2 , G). Since trade data come at the same level
of aggregation, with exporters/importers spread within provinces’ boundaries, the lack of
geographical detail on roads does not strike us as critical.
For our empirical analysis, however, we need a measure of provincial access to gateways.
We obtained shortest road distances distpg and the associated routes Jpg between provincial
centers from Google Maps. Jpg is the set of provinces one has to traverse on the shortest
distance route between p and g, including the origin and the destination. In figure 3, JP1 ,G =
(P1 , P2 , G) and distP1 ,G is the length of the road connecting P1 and G through P2 .
In order to visualize the road network and its upgrading, we use map data provided
by user-supplied online sources plotted at the bottom two panels of figure 1, which visibly
showcase the extensive and geographically comprehensive nature of road upgrades.5 We now
describe and analyze the basic features of our data.
2.3
Preliminary Analysis
Table 1 summarizes key descriptive statistics from our data. Regardless of the unit of observation (province-gateway, province-gateway-country, or province-gateway-industry), exports
and imports both increased substantially between 2003 and 2012. Data also show a striking
increase in the share of expressways in total road stock within provincial boundaries: its
mean increased by more than three-fold in 10 years from 9 percent in 2003 to 31 percent in
2012.
The third panel of table 1 shows the extensive margins of the observed trade increase.
Average number of gateways per province increased from 7.5 in 2003 to 12.2 in 2012 for
5
We cross-checked these maps against lower resolution maps published by the General Directorate of
Highways (available from authors upon request) and found discrepancies only in a few segments. We did
not use it in our analysis because it is not official data, the discrepancies were more prevalent in the remote
eastern provinces which benefited most from the investment, and the resolution proved to be inadequate for
analysis on standard GIS packages.
7
export flows, and from 7.2 to 9.2 for import flows. Similarly, the average number of foreign
countries per province increased from 92.7 in 2003 to 105.6 for exports, and from 55.1 to 73.2
for imports. The average number of 2-digit ISIC industries per province increased by about
2.5 for both exports and imports over the same period. These patterns suggest that the
expansion of road capacity between 2003-2012 may have affected regional trade on intensive
as well as on extensive margins.
Since our empirical analysis will exploit province-gateway flows, it is important to note
that it is not just the nearest gateway that matters for a province’s foreign trade. Ports and
border crossings are specialized in industries and trade partners: an overwhelming majority
of trade in a certain industry with a certain country goes through a single port. This
specialization is consistent with both geography—the border crossing to Syria is irrelevant
for trade with Germany—and logistics technology—there are strong increasing returns at
ports due to containerization and industry-specific port equipment. The bottom panel of
table 1 reports high gateway concentration measures for industry- and country-level flows
to and from provinces. With this in mind, it is important to consider all existing or newly
formed pg links during our data period.
As a first pass at the data, we plot the period change in province-level trade between
2003 and 2012 against a proxy that captures the road quality improvement of a province in
accessing foreign markets over the same period. We construct the proxy as follows. For each
pg pair, we calculate the expressway road share on the shortest distance route Jpg :6
∑
erspgt = ∑
j∈Jpg
j∈Jpg
expresswayjt
roadStockj,2003
.
We then aggregate erspgt at the province level, using the 2003-2012 average share of each
gateway in that province’s total trade flows, πpg . The period road quality improvement in
6
We fix the denominator, the length of total road stock, in the initial year. Additions to the road network
are quantitatively small over this time period (see figure 2), and more importantly, all upgrades were done
on single carriageways that were in operation as of 2003. To be conceptually consistent with this, we fix the
initial stock. The results are robust to using yearly values for the denominator, which shows slight variation.
8
accessing foreign markets is given by
∑
πpg · (erspg,2012 − erspg,2003 ).
g
Figure 4 shows a positive relationship between this variable and the change in province-level
trade over the 2003-2012 period; that is, provinces that experienced a greater improvement
in their connectivity to the country’s international gateways posted a higher increase in their
trade flows between 2003 and 2012. The slope of the regression line plotted in the figure is
4.2 with a p-value of 0.06.
Before moving on to the main empirical analysis, we note that for the purpose of estimating the transport-cost reducing impact of expressways, it would have been ideal to also have
data on domestic trade between cities. Such information, however, is typically not available
for developing countries. Observing the domestic components of export/import shipments
thus provides us with limited but useful information to estimate how such flows are generally
affected by transport infrastructure. With 20 gateway provinces as “origins” of imports to
81 provinces and as “destinations” of exports from provinces, our data can be fit with a
simple gravity model. Table 2 reports the results of a gravity equation estimated from our
data. Using and province- and gateway-flow fixed effects (in a way that is reminiscent of
exporter and importer fixed effects in international gravity estimations), we estimate the
distance elasticity of flows separately at the beginning (2003/04) and at the end (2011/12)
of the period under consideration. Excluding own-shipments for p = g with dist = 0, i.e.
exports and imports of gateway provinces through their own ports, there are 3, 200 possible
flows in our data (= 81 × 20 × 2 − 20 × 2). The OLS estimates in the first two columns
use positive flows only. The much higher number of observations in the 2011/12 sample is a
manifestation of the extensive margin increase documented in table 1.
Given the pervasiveness of zero flows and the well-known problems associated with using
OLS to estimate gravity models (Santos-Silva and Tenreyro, 2006; Head and Mayer, 2013a),
9
we also use a Poisson pseudo-maximum likelihood (PPML) estimator in third and fourth
columns.7 Consistent with the well-documented pattern in the literature, our PPML estimates of distance elasticity are smaller in absolute value than the respective OLS estimates.
The estimates fall in the acceptable range of distance elasticities reported by Head and Mayer
(2013b). Comparing the estimates for 2003/04 and 2011/12, we see that the elasticity estimated for the latter period is smaller in absolute value: a one percent increase in distance
decreases trade by 1.4 percent in in the beginning of the period while it decreases trade by
1.2 percent at the end of the period, implying a reduction in distance elasticity of about 14
percent. We now move on to our main empirical analysis.
3
Empirical Analysis
To derive our estimating equation, we specify bilateral trade flows between province p and
gateway g in a general gravity setting:
f
f
−θ
tradefpgt = ωpt
· ωgt
· T Cpgt
,
(1)
f
where ωpt
captures time-varying province-level variables that affect its exports/imports, and
f
ωgt
captures time-varying factors that affect international demand and supply through gate g
(such as income in destination countries that can be reached through g). T Cpgt is the cost of
transportation and θ > 0 denotes the elasticity of trade flows with respect to transportation
costs.
The cost of transportation at time t is a function of the distance and the quality of roads
connecting the pg pair:
τe ·erspgt +τs ·(1−erspgt )
T Cpgt = distpg
,
(2)
where τe , τs are distance elasticities associated with new expressways and old single7
Number of observations in these columns falls short of 3,200 because the PPML routine drops exporters
(importer) with no positive trade flows with any partner in the presence of exporter (importer) fixed effects.
10
carriageway roads, respectively. The route-specific expressway road share (erspgt ) defined
above is the weight of τe in the average distance elasticity. We can rearrange (2) to obtain
T Cpgt = distτpg(1−erspgt ) · distτpge ,
(3)
where τ = τs − τe . Time-variation in T C is driven by changes in ers over time, captured
by the first term in (3). To gauge the long-term effect of increasing erspgt on trade flows,
we substitute T Cpgt from (3) into (1), take the natural logarithm and calculate the longdifference as
∆ ln(tradefpg ) = ∆ ln(ωpf ) + ∆ ln(ωgf ) − θτ · [∆(1 − erspg )] · ln [distpg ] ,
(4)
where ∆x denotes the difference between 2003 and 2012 of a variable. Note that the timeinvariant term distτpge in (3) drops when we take long-differences. Rearranging and relabeling
terms, we write (4) as
∆ ln(tradefpg ) = ∆ ln(ωpf ) + ∆ ln(ωgf ) + β · [∆(erspg − 1)] · ln [distpg ] ,
(5)
where β = θτ . Since expressway road share increased in all routes, ∆(erspg − 1) > 0. To
reflect this improvement, we denote
∆RCpg = ∆(erspg − 1) · ln [distpg ] ,
as the change in road capacity. Our data allow us to calculate ∆RCpg for all pg pairs. Note
that if transport costs on expressways are less distance elastic than on single carriageways
roads, i.e., if τs > τe , an increase in road capacity RC through higher ers will reduce
transport cost T C and increase trade in (1). We are now ready to test this relationship.
11
3.1
Road Capacity and Trade
The estimating equation follows from (5):
∆ ln(tradefpg ) = δpf + δgf + β · ∆RCpg + ϵpg ,
(6)
where (δpf , δgf ) are gateway- and province-flow fixed effects. As in the gravity literature, the
parameter of interest τ cannot be separately identified from the elasticity θ of trade flows to
trade costs. In what follows, we present β coefficients estimated from various specifications
of (6) and use θ = 4 based on Simonovska and Waugh (2013) to back out τ = β/θ.
Table 3 presents the first set of results. The OLS estimate of β = 0.629 is significant
at the 5% level. The implied τ = 0.16 is consistent with the drop in distance elasticity
over this time period presented in table 2. To give a sense of magnitudes, suppose that the
PPML estimate from 2003-2004 (column 3 of table 2) is equal to τs = 1.384, as expressway
road share was rather low at the beginning of our sample. With τ = τs − τe = 0.16, this
implies τe = τs − 0.16 = 1.224. We use these elasticities in the transport cost function 2 to
calculate the cost of shipping over the mean pg distance of 820 km in our data when the
road covering that distance is single carriageway versus expressway. We find that the cost of
an average-distance shipment drops by 65% if the complete route is upgraded from a single
carriageway. This is a significant drop in transport costs.8
In the next column, we rely on the instrumental variables approach to address potential
omitted variable bias. We documented that the primary motivation behind the investment
program was to relieve congestion and reduce the high rate of road accidents. This partly
alleviates endogeneity concerns. Also, first-differencing implicitly controls for any timeinvarying pg level factors that might be correlated with the error term. Still, under a less
likely scenario, policy-makers could decide to favor some routes over others, for instance
because there already existed strong exporters located in p trying to reach a particular
8
In the TC function, we set dist = 820. Initially the share of expressways is zero, ers = 0, and the
corresponding value of T C is distτs = 10, 782.5; and for ers = 1, it is distτe = 3, 685.6.
12
gateway g. To address such concerns, we estimate an IV model, using the initial share of
expressways along pg routes as an instrument. In doing so, we follow the literature estimating
the impact of trade liberalization using as instrument initial tariff levels, (e.g. Goldberg and
Pavcnik 2005; Amiti and Konings 2007; Topalova 2010). Initial road capacity is a valid and
informative instrument for the change in road capacity over the period under consideration
because of the following. First, the large-scale public investment program in Turkey aimed
at upgrading into expressways all the roads connecting the country to international markets
and those connecting provincial centers.9 Since our measure of road capacity relies on the
idea that road infrastructure is shared, we should expect the final share of expressways
along different routes to converge to a given target, controlling for the initial conditions in
the province and gateway. This has two implications. First the dispersion in the share of
expressways across pg routes decreased over the 2003-2012 period: the coefficient of variation
fell from 0.35 in 2003 to 0.16 in 2012. Second, given that all routes converged to a target level
over 2003-2012, the initial share of expressways becomes a good predictor of its change over
this period. This is illustrated in figure 5: higher initial shares of expressways are associated
with smaller changes over the 2003-2012 period. The regression line has a slope of -0.6 that
is significant at the one percent level.
We estimate a two-stage least squares model, instrumenting the period change in road
capacity along a pg route with the initial share of expressways along the route. In the first
stage, we estimate the following:
∆RCpg = γp + γg + α1 ln distpg + α2 ers2003
+ ηpg .
pg
(7)
It is worth noting that the equation above is not estimated in differences, thus, unlike
equation (6), ln distpg does not drop out. First-stage results are presented in column 3 of
¨
˙
˙
˙ ¸ IM
˙
See the bottom bullet point in page 55 of the policy document “TURK
IYE
ULAS¸IM VE ILET
IS
˙
˙
STRATEJISI-HEDEF 2023” published by the Ministry of Transport, Maritime and Communications of
the Republic of Turkey, available at http://www.izmiriplanliyorum.org/static/upload/file/
turkiye_2023_ulasim_ve_iletisim_stratejisi.pdf.
9
13
table 3. Consistent with the pattern in figure 5, the period change in road capacity and the
initial share of expressways are negatively related. Results also show that bilaterally more
distant pg pairs benefited more from the capacity expansion over the 2003-2012 period.
Column 2 of the same table presents the estimation results from the second-stage. The
estimated coefficient on ∆RCpg is still significant at the 5% level and larger in magnitude:
the implied size of τ from IV is 0.21, which compares to its OLS estimate of 0.16. A backof-the-envelope calculation similar to the one done for the OLS estimate of τ implies that
transforming all single carriage roads into expressways reduces the cost of shipping over the
mean pg distance in our data by 75%.
The results so far are based on observations with positive trade flows at both the beginning
and end of our data period. There are only 1,015 such observations out of all 3,200 possible
pgf triplets, excluding p = g pairs. In table 1, we documented the extensive margins of the
trade increase as well as the gateway specialization in trade partners. The foreign trade of
many provinces increased during this time period due to the initiation of new trade flows
with partner countries through new gateways. To check whether road capacity improvements
can explain such new links, we estimate a linear probability model in which we replace the
dependent variable in equation (6) with a binary variable N ewpg that takes the value one if a
new province-gateway trade link has started, i.e., tradefpg turns from zero in 2003 to positive
in 2012, and zero otherwise. Columns 4 and 5 present the results.10 According to our IV
estimate (column 5), a one percent increase in road capacity increases the probability that a
new trade link is established by 0.37. Give the specialization of parts as documented in table
1, a new trade link between a pg pair implies that province p can export to new destinations
and/or export in new industries. Later we will investigate the importance of these extensive
margins in more detail.
Given the importance of enhancements in road capacity in establishing new trade links,
10
Probit and IVProbit estimates are qualitatively and quantitatively similar to LPM and IVLPM estimates. The reason we report the latter is that linear models provide a more flexible approach in the presence
of many fixed effects. Probit and IVProbit results are available from the authors.
14
one may ask whether the elasticity of trade flows estimated from the intensive margin is
subject to any selection bias. In other words, we should check whether the previously
estimated coefficient on ∆RCpg is subject to selection bias arising from the fact that it
is based on a sample of pg pairs that have always traded with each other over the 20032012 period. To answer this question, we follow the approach suggested by Mulligan and
Rubinstein (2008). Firstly, we estimate the probability that we observe positive trade for
a pg pair in both 2003 and 2012, and obtain predicted selection probabilities. Next, we
estimate equation (6) on subsamples determined by the predicted selection probabilities,
i.e. subsamples of pg pairs with the predicted probabilities above the 20th, 30th, and 40th
percentiles of the selection probability distribution. If our estimate of the intensive margin
elasticity of trade flows with respect to road capacity is not subject to serious selection
bias, then the estimates of the intensive margin elasticity we obtain for different subsamples
should be close to the one we obtain for the whole sample. First column of table 4 shows that,
after controlling for importer and exporter fixed effects, the probability of observing positive
trade for a pg pair in both years decreases with the bilateral distance between them but it
is not significantly associated with road expansion over the 2003-2012 period. Columns 3 to
5 show the results obtained from the estimation of equation (6) on subsamples of pg pairs
with the predicted probabilities above the 20th, 30th, and 40th percentiles. The estimates of
the intensive margin elasticity of trade flows with respect to road capacity are very similar
to the one obtained on the whole sample (column 2). The coefficient estimates in columns
3-5 are not statistically different from the one presented in column 1. So, we conclude that
our estimate of the intensive margin elasticity of trade flows with respect to road capacity
is not subject to serious selection bias.
Our results so far imply that expanding road capacity reduces distance elasticity of trade,
increasing the volume of existing trade flows and establishing new trade links. We now
look into other margins of the observed trade expansion at the pg-level, namely the country
(trade partner) and industry dimensions of our data. We decompose pg-level trade into the
15
number of countries or industries traded, and the average volume of trade per pgc or pgi.
We estimate equation (6) for both margins. Panels A and B of table 5 present intensive and
extensive margin decompositions for countries and industries, respectively. A higher than
average improvement in province-gateway road connectivity increases the number of both
countries and industries with positive flows at those pairs at the extensive margin (columns
3 and 4 in both panels). In the intensive margin, pgc-level effects are significant (columns
1 and 2 in panel A) and consistent with our baseline results. At the industry dimension,
however, the intensive margin is insignificant despite having the right sign. To sum up, our
results point to three mechanisms as relevant drivers behind the pattern we observe at the
pg-level. The expansion of road capacity, which reduced distance elasticity of trade, led to
an increase in the number of countries traded, average volume of trade per country, and the
number of industries traded. In the following subsection, we will investigate the importance
of the industry margin in more detail as this margin is highly relevant for shaping regional
comparative advantage.
3.2
Road Capacity and Transportation Intensive Industries
Having documented the trade-enhancing effect of expressway construction, we now explore
a potential channel through which this increase may have materialized. One would expect
improved road capacity to have a bigger impact on trade the more transportation-intensive
an industry is. This may be due to two industry characteristics: sensitivity to the length
and precision of delivery times, and the heaviness of an industry’s output.
For some agricultural goods, time-sensitivity may arise simply due to perishability. The
literature recognizes other causes as well: for intermediate goods that are part of international supply chains, timeliness and predictability of delivery times are crucial. Industries
with volatile demand for customized products display high demand for fast and frequent
shipments of small volumes (Evans and Harrigan 2005). Time-in-transit also constitutes a
direct inventory-holding cost itself. Using data on US imports disaggregated by mode of
16
transportation, Hummels and Schaur (2013) exploit the variation in the premium paid for
air shipping and in time lags for ocean transit to identify the consumer’s valuation of time.
They estimate an ad valorem tariff of 0.6-2.3 percent for each day in transit.
In our setting, one of the components of the domestic LPI (described in section 2) is
“export lead time,” which measures the time it takes to transport goods from the point of
origin to ports. The LPI data show that the median export lead time in Turkey decreased
from 2.5 days in 2007 to 2 days in 2012, marking an improvement relative to the best
performer (Singapore). Considering time as a trade cost, such evidence further motivates us
to test the hypothesis that capacity-enhancing investment in road infrastructure in Turkey
contributed to increased regional foreign trade during the 2003-2012 period.
Heaviness is another determinant of how transportation intensive an industry is. Duranton, Morrow, and Turner (2013) estimate the effect of the US highway system on the
value and composition of trade between US cities, and find that cities with more highways
specialize in sectors producing heavy goods.
In what follows, we use a measure of time-sensitivity guided by the empirical literature
investigating the mode of shipping decisions in international trade. As Hummels and Schaur
(2013) demonstrate, exporters pay a premium for expensive yet fast air cargo, depending
on the value that consumers attach to fast delivery. Motivated by this observation, we use
the air share of industry i imports into a country other than Turkey. In particular, we use
imports into the United Kingdom in 2005. We measure heaviness by the weight-to-value
ratio of industry imports into the United Kingdom in 2005.11 In particular, we define Airi
and Heavyi as follows:
air vali
Airi =
air vali + ves vali
(
,
Heavyi = ln
ves wgti
ves vali
)
(8)
where air vali denotes the value of air shipments into the United Kingdom in industry i
11
We obtain similar results using US import data. To preserve space, we only report the results based on
UK imports. Alternative results are available from the authors upon request.
17
in 2005, and ves vali (ves wgti ) the value (weight) of shipments by ocean vessel. Table 6
reports both variables for all 24 industries. As expected, these two measures are negatively
correlated. When we regress Airi on Heavyi , the coefficient is −0.158 with a t-statistic of
−4.94 and a good fit (R2 = 0.53)—air shipping is less suitable for goods with a high weightto-value ratio (Harrigan 2010). Therefore, air share of an industry can be a proxy for its
time-sensitivity only if its heaviness is controlled for.
Our next specification interacts these variables with the change in road capacity:
f
∆ ln(tradefpgi ) = δpg
+α·∆ ln(RCpg )×Θi +γa ·∆ ln(RCpg )×Airi +γh ·∆ ln(RCpg )×Heavyi +ϵpgi .
(9)
Here long-term differencing eliminates industry fixed effects which may be driving air shares
for reasons other than the time-sensitivity of industries. If provinces with a higher increase
in road capacity experienced a larger increase in the trade of time-sensitive and heavy goods,
the coefficients γa and γh will be positive.
An important factor to consider in this exercise is that transport intensity of an industry
may be systematically related to its elasticity of trade flows to trade costs. For instance,
if varieties are more substitutable in industries with higher air share, our time sensitivity
measure could be picking up differential price elasticities. To address this concern, we control
in equation (9) for the interaction between road capacity changes and industry-level elasticity
of substitution Θi estimated by Broda and Weinstein (2006).12 A higher Θi implies greater
price elasticity. We expect α < 0 if transport cost reductions induced by road capacity
expansions increase trade relatively more in industries with higher elasticity of substitution.
Results are presented in table 7. All specifications use the instrumental variable method
and cluster standard errors at the province-gateway level. As we argued above, controlling
12
We use trade elasticities at the HS10 level estimated by Soderberry (2013). Using as a bridge the HS10SIC concordance by Pierce and Schott (2012) and the SIC-ISIC Rev. 3 concordance by the United Nations
Statistics Division (http://unstats.un.org/unsd/cr/registry/regdnld.asp?Lg=1), we map it to
4 digit ISIC industries. Since our industry aggregation is at the 2 digit level, we use the median elasticity
within broader industry groupings.
18
for heaviness is important for air shares to capture the time-sensitivity of industries. Third
column is thus our preferred specification. For transparency, we also present the interactions
with air share and heaviness separately in the first two columns. In the fourth column, we
use the time sensitivity estimates from Hummels and Schaur (2013). The results confirm the
hypothesis that province-gateway routes with greater road capacity expansions experienced
a larger trade increase in time sensitive and heavy goods.
The stronger response in sectors that are expected to be more sensitive to road quality adds
credibility to the claim that we are identifying the effect of reductions in transportation costs
on exports. While we argued that endogenous selection is not a major concern in our setting,
this claim can be made even stronger for the evidence presented here. It is very unlikely that
planners prioritize investments in a province because of anticipated trade growth in certain
products.
Of course, the aggregate export response of an industry is also a function of its initial
location: if transport intensive industries were initially agglomerated in provinces that had
good market access to begin with (see figure 4), they would gain relatively little from transport cost reductions.13 Thus, the long term effect of the infrastructure investment could be
more drastic if transport intensive industries endogenously locate towards the interior of the
country, which now has better market access.
Finally, we test whether fall in transport costs, caused by road capacity enhancements,
increased the probability that pg pairs start trading in transport-sensitive industries. To do
so, we estimate an equation similar to equation (9) replacing the dependent variable with
a binary variable that takes on the value one if a pg pair trading in industry i in the postinvestment period did not do so in the pre-investment period, and zero otherwise. Since
this equation is not estimated in differences, we also control for industry fixed effects. Table
8 shows the estimation results. In column 1, there is (weak) evidence that pg pairs that
experienced a greater reduction in bilateral transport costs are more likely to start trading
13
The possibility of such selection should not cause any bias in our estimates as we are using long-term
differences – which eliminate any time-invariant province-industry factors such as location.
19
in time-sensitive industries relative to other industries. This result survives in column 3
which adds an interaction of ∆ ln(RCpg ) and Heavyi on the right-hand side. Nevertheless,
there is no evidence that road capacity enhancements increase the probability that pg pairs
start trading in heavy industries compared to other industries. These results point to the
role of internal trade costs in shaping regional comparative advantage within countries.
4
Conclusion
This study investigates the effect of Turkey’s large-scale investment in the quality and capacity of its road transportation network on the level and composition of international trade
associated with subnational regions within Turkey. Transport cost reductions brought about
by this investment led to increased trade with regions whose connectivity to the international
gateways of the country improved most, the main channels being increase in the countries
traded, average volume of trade per country, the number of industries traded. Our results
thus support the idea that internal transportation infrastructure may play an important role
in accessing international markets.
A particular channel for this regional response appears to be increased exports of
transportation-intensive goods from regions that experienced the largest drop in transport
costs. In particular, time-sensitivity of an industry matters for the effect of transport costs
on the industry-level exports. This is in line with the recent empirical literature emphasizing
time costs in international trade. While existing studies typically emphasize time in transit
between countries or time lost in customs, our results highlight the importance of domestic
transportation infrastructure in moving goods from the factory gate to the ports in a timely
and predictable fashion. To the extent that efficient logistics in time-sensitive goods enable
countries to take part in global supply chains and exploit their comparative advantages, our
findings have important developmental implications.
Finally, note that this study focused on short-run effects by treating firm locations as
20
fixed. Economic activity, however, could relocate in response to the changing relative costs
of reaching major internal and international markets from various regions. Many economic
geography models suggest that the direction of this change depends on the relative strength
of agglomeration forces versus trade costs, making it hard to predict. The long term impact
of this large-scale infrastructure project on regional outcomes such as population, wages and
welfare thus remains an interesting avenue for future research.
References
ADBI (2009): “Infrastructure for a Seamless Asia,” Discussion paper, Asian Development
Bank Institute, Tokyo.
Allen, T., and C. Arkolakis (2014): “Trade and the Topography of the Spatial Economy,” Quarterly Journal of Economics.
Amiti, M., and J. Konings (2007): “Trade Liberalization, Intermediate Inputs, and Productivity: Evidence from Indonesia,” American Economic Review, 97(5), 1611–1638.
Anderson, J. E., and E. van Wincoop (2004): “Trade Costs,” Journal of Economic
Literature, 42(3), 691–751.
Atkin, D., and D. Donaldson (2014): “Who’s Getting Globalized? The Size and Nature
of Intranational Trade Costs,” UCLA mimeo.
Broda, C., and D. E. Weinstein (2006): “Globalization and the Gains from Variety,”
The Quarterly Journal of Economics, pp. 541–585.
Cos¸ar, A. K., and P. Fajgelbaum (2014): “Internal Geography, International Trade,
and Regional Specialization,” forthcoming, American Economic Journal Microeconomics.
Demir, B. (2011): “Transport Costs and Turkey’s International Trade,” Background Paper
for Turkey Transport Sector Expenditure Review (2012).
Donaldson, D. (2012): “Railroads of the Raj: Estimating the Impact of Transportation
Infrastructure,” NBER Working Paper No. w16487.
Donaldson, D., and R. Hornbeck (2013): “Railroads and American Economic Growth:
A Market Access Approach,” NBER Working Paper No. w19213.
Duranton, G., P. Morrow, and M. A. Turner (2013): “Roads and Trade: Evidence
from the US.,” forthcoming, The Review of Economic Studies.
21
Evans, C. L., and J. Harrigan (2005): “Distance, Time, and Specialization: Lean
Retailing in General Equilibrium,” American Economic Review, pp. 292–313.
GDH (2012): “Turkish General Directorate Of Highways, Highway Transportation
Statistics,” Website, http://www.kgm.gov.tr/SiteCollectionDocuments/KGMdocuments/
Yayinlar/YayinPdf/KarayoluUlasimIstatistikleri2012.pdf.
(2014):
“Turkish General Directorate Of Highways, Divided Highway Projects,” Website, http://translate.google.com/translate?hl=en&sl=tr&tl=en&
u=http://www.kgm.gov.tr/Sayfalar/KGM/SiteTr/Projeler/Projeler-BolunmusYol.aspx.
Goldberg, P. K., and N. Pavcnik (2005): “Trade, wages, and the political economy of
trade protection: evidence from the Colombian trade reforms,” Journal of International
Economics, 66(1), 75–105.
Harrigan, J. (2010): “Airplanes and Comparative Advantage,” Journal of International
Economics, 82(2), 181–194.
Head, K., and T. Mayer (2013a): “Gravity Equations: Workhorse, Toolkit, and Cookbook,” CEPR Discussion Papers 9322, C.E.P.R. Discussion Papers.
(2013b): “What separates us? Sources of resistance to globalization,” Canadian
Journal of Economics/Revue canadienne d’conomique, 46(4), 1196–1231.
Hummels, D., and G. Schaur (2013): “Time as a Trade Barrier,” American Economic
Review, 103(7), 2935–59.
IADB (2013): “Too Far to Export: Domestic Transport Costs and Regional Export Disparities in Latin America and the Caribbean,” Discussion paper, Inter-American Development
Bank, Washington, DC.
Limao, N., and A. J. Venables (2001): “Infrastructure, Geographical Disadvantage,
Transport costs, and Trade,” The World Bank Economic Review, 15(3), 451–479.
Mulligan, C. B., and Y. Rubinstein (2008): “Selection, Investment, and Women’s
Relative Wages Over Time,” The Quarterly Journal of Economics, 123(3), 1061–1110.
Pierce, J. R., and P. K. Schott (2012): “A concordance between ten-digit US Harmonized System Codes and SIC/NAICS product classes and industries,” Journal of Economic
and Social Measurement, 37(1), 61–96.
Redding, S., and A. J. Venables (2004): “Economic Geography and International Inequality,” Journal of international Economics, 62(1), 53–82.
Rousslang, D. J., and T. To (1993): “Domestic Trade and Transportation Costs as
Barriers to International Trade,” Canadian Journal of Economics, pp. 208–221.
Santos-Silva, J. M. C., and S. Tenreyro (2006): “The Log of Gravity,” The Review
of Economics and Statistics, 88(4), 641–658.
22
Simonovska, I., and M. Waugh (2013): “The Elasticity of Trade: Estimates and Evidence,” Journal of International Economics.
Soderberry, A. (2013): “Estimating Import Supply and Demand Elasticities: Analysis
and Implications,” forthcoming, Journal of International Economics.
Topalova, P. (2010): “Factor Immobility and Regional Impacts of Trade Liberalization:
Evidence on Poverty from India,” American Economic Journal: Applied Economics, 2(4),
1–41.
Volpe Martincus, C., and J. Blyde (2013): “Shaky Roads and Trembling Exports:
Assessing the Trade Effects of Domestic Infrastructure Using a Natural Experiment,”
Journal of International Economics, 90(1), 148–161.
Volpe Martincus, C., J. Carballo, and A. Cusolito (2013): “Routes, Exports and
Employment in Developing Countries: Following the Trace of the Inca Roads,” InterAmerican Development Bank, mimeo.
WB (2009): “World Development Report: Reshaping Economic Geography,” Discussion
paper, World Bank, Washington, DC.
WTO (2004): “World Trade Report 2004: Exploring the linkage between the domestic
policy environment and international trade,” Report WTO/WTR/2004, World Trade Organization (WTO), Geneva.
Yeaple, S., and S. Golub (2007): “International Productivity Differences, Infrastructure,
and Comparative Advantage,” Review of International Economics, 15(2), 223–242.
23
Figure 1: Turkish Provinces and Roads
Provincial Boundaries and Centers
Road network in 2002
Road network in 2012
Notes: The top panel outlines provincial boundaries, provincial centers (orange nodes), and the top five gateway provinces
(those labeled and marked with green diamonds). In the second and third panels, red lines are single carriageway roads and
black lines are expressways. Geographical data used to plot the roads is downloaded from http://www.diva-gis.org.
Total road stock
20
12
20
10
20
08
20
06
20
04
20
02
20
00
19
98
19
96
19
94
19
92
19
90
19
88
19
86
70
65
60
55
50
45
40
35
30
25
20
15
10
5
0
19
84
1000 Kilometers
Figure 2: Roads over Time
Expressways
Notes: This figure plots total length of intercity roads and expressways between 1984-2002. The y-axis in
thousand kilometers.
Figure 3: Data Description: Provinces, Roads and Expressways
G
P2
P1
Notes: This illustration helps to describe the data. The tiles represent provincial boundaries, with (P1 , P2 , G)
nodes representing provincial centers. G stands for gateway. Red lines are single carriage roads and black
lines are dual carriage expressways. See text for details.
25
4
2
−2
0
Change in ln(Trade)
6
Figure 4: Road Capacity Improvements and Change in Trade Flows
.1
.2
.3
Change in Weighted ers
95% Confidence Interval
.4
.5
Fitted values
Notes:
∑ The x-axis is the change in each province’s connectivity to gateways over the 2003-2012 period defined
as g πpg · ∆erspg , where πpg is the share of gateway g in province p’s total trade in 2003 and 2012 and
∆erspg is the change in the share of expressways in total road stock on the route between p and g between
2003 and 2012 – capturing the road quality improvement for a province in accessing foreign markets. The
y-axis is the period change in the logarithm of the sum of exports and imports of province p. The slope of
the regression line in the figure is 4.2 with a p-value of 0.06.
Figure 5: Period Change in the Share of Expressways and Its Initial Value
.3
.1
.2
Change in ers
.4
.5
Fitted values
0
.05
.1
Initial ers
.15
.2
Notes: The slope of the regression line in the figure is -0.6 and is significant at the one percent level.
26
Table 1: Summary Statistics
Trade statistics (in 1,000 USD)
Exports in 2003
Exports in 2012
Imports in 2003
Imports in 2012
∆ ln(exports)
∆ ln(imports)
Distance (km, across pg pairs)
Expressway share in total
road stock across provinces
in 2003
in 2012
Extensive margins
Per province # of
gateways, exports in 2003
gateways, exports in 2012
gateways, imports in 2003
gateways, imports in 2012
countries, exports in 2003
countries, exports in 2012
countries, imports in 2003
countries, imports in 2012
industries, exports in 2003
industries, exports in 2012
industries, imports in 2003
industries, imports in 2012
Gateway specialization measures
Hcexp in 2003
Hcexp in 2012
Hcimp in 2003
Hcimp in 2012
Hiexp in 2003
Hiexp in 2012
Hiimp in 2003
Hiimp in 2012
pg sample
Mean
Std
72,600
776,000
148,000 1,780,000
98,000 1,120,000
245,000 2,580,000
1.692
2.111
1.486
2.169
820
422
0.085
0.305
0.067
0.119
7.519
12.188
7.163
9.247
72.739
105.658
55.088
73.169
17.164
19.911
17.295
19.647
4.051
4.537
3.354
3.727
46.644
48.821
36.570
42.685
5.580
4.305
5.695
4.489
0.452
0.364
0.585
0.527
0.418
0.345
0.437
0.434
0.230
0.185
0.293
0.287
0.197
0.176
0.194
0.224
pgd sample
Mean
Std
4,603 53,400
8,431 101,000
7,856 81,400
16,100 178,000
1.478
2.182
1.168
2.423
Notes: The measure of specialization is a simple Herfindahl index calculated as follows:
∑
s2gc ,
Hc =
g
where sgc is the share of exports to destination c going through gateway g. Similarly,
∑
s2gi ,
Hi =
g
where sgi is the share of exports in industry i going through gateway g.
27
pgi sample
Mean
Std
9,634 117,000
17,600 238,000
14,500 149,000
32,000 309,000
1.790
2.484
1.361
2.359
Table 2: Gravity Estimation
(1)
(2)
ln(tradefpg )
∗∗∗
ln distpg
-1.858
(0.084)
OLS
2003-04
p-f,g-f
1,376
0.638
Regression
Sample
Fixed effects
Observations
R2
(3)
(4)
tradefpg
-1.724∗∗∗
(0.076)
OLS
2011-12
p-f,g-f
1,719
0.655
-1.384∗∗∗
(0.086)
PPML
2003-04
p-f,g-f
2,686
0.981
-1.219∗∗∗
(0.078)
PPML
2011-12
p-f,g-f
2,686
0.972
Notes: All regressions are estimated with province-flow and gateway-flow fixed effects, where flows are
exports or imports. Robust standard errors in parentheses. Significance: * 10 percent, ** 5 percent, ***
1 percent.
Table 3: Total Trade and New Trade Links
∆RCpg
(1)
∆ ln(tradefpg )
(2)
∆ ln(tradefpg )
0.629∗∗
(0.278)
0.834∗∗
(0.350)
(3)
∆RCpg
(4)
f
N ewpg
(5)
f
N ewpg
0.0775∗∗
(0.0349)
0.368∗∗
(0.183)
ers2003
pg
-0.144∗∗∗
(0.0254)
ln distpg
0.245∗∗∗
(0.0096)
First stage
p-f,g-f
1,015
-0.0025
(0.0134)
LPM
p-f,g-f
3,200
0.0542
(0.0382)
IV
p-f,g-f
3,200
0.662
0.153
0.133
Regression
Fixed Effects
Observations
Anderson-Rubin χ2 (2)
R2
OLS
p-f,g-f
1,015
0.339
IV
p-f,g-f
1,015
6.67
0.338
ost
re
Notes: N ewpg is equal to P r(tradef,P
> 0&tradef,P
= 0). Robust standard errors in parentheses. Significance:
pg
pg
* 10 percent, ** 5 percent, *** 1 percent.
28
Table 4: Heterogeneity of Trade Flows
(1)
Selectfpg
(2)
∆ ln(tradefpg )
(3)
∆ ln(tradefpg )
(4)
∆ ln(tradefpg )
(5)
∆ ln(tradefpg )
∆RCpg
-0.141
(0.159)
0.834∗∗
(0.350)
0.838∗∗
(0.350)
0.831∗∗∗
(0.349)
0.852∗∗∗
(0.352)
ln distpg
-0.159∗∗∗
(0.0327)
LPM-IV
All
p-f,g-f
3,200
0.544
IV
All
p-f,g-f
1,015
0.338
IV
20th
p-f,g-f
1,012
0.336
IV
30th
p-f,g-f
1004
0.344
IV
40th
p-f,g-f
992
0.348
Regression
Sample
Fixed Effects
Observations
R2
Notes: Selectpg is an indicator variable that is equal to one if 2003 and 2012 trade flows are both positive, and zero otherwise. Sample in
columns 3-5 are constructed based on the predicted probabilities from column (1). Robust standard errors in parentheses. Significance:
* 10 percent, ** 5 percent, *** 1 percent.
Table 5: Trade Partner and Industry Margins of Trade
(1)
(2)
f
∆ln(tradefpg /Npg
)
(3)
(4)
f,2012
f,2003
f,2012
f,2003
(Npg
− Npg
)/(Npg
+ Npg
)
Panel A: Countries
∆RCpg
Observations
R2
0.442∗
(0.236)
1,015
0.320
0.603∗∗
(0.298)
1,015
0.319
0.163∗∗∗
(0.054)
1,807
0.981
0.412∗∗∗
(0.078)
1,807
0.972
0.254
(0.252)
1,011
0.273
OLS
Intensive
p-f,g-f
0.117
(0.310)
1,011
0.272
IV
Intensive
p-f,g-f
0.156∗∗∗
(0.054)
1,801
0.299
OLS
Extensive
p-f,g-f
0.520∗∗∗
(0.078)
1,801
0.279
IV
Extensive
p-f,g-f
Panel B: Industries
∆RCpg
Observations
R2
Regression
Sample
Fixed Effects
f,t
Notes: In Panel A, Npg
denotes the number of countries with positive trade flows (exports or imports) at the pglevel at time t. In Panel B, it denotes the number of industries. Robust standard errors in parentheses. Significance:
* 10 percent, ** 5 percent, *** 1 percent.
29
Table 6: Air Shares and Heaviness of Industries
ISIC Rev.3
01
35
33
31
32
36
30
29
24
28
22
18
19
17
25
34
26
13
15
27
16
21
20
23
Industry
Airi
Heavyi
Agriculture, hunting and related
Other transport equipment
Medical, precision and optical instruments, watches, and clocks
Electrical machinery and apparatus n.e.c.
Radio, television and communication equipment and apparatus
Furniture; manufacturing n.e.c.
Office, accounting and computing machinery
Machinery and equipment n.e.c.
Chemicals and chemical products
Fabricated metal products, except machinery and equipment
Publishing, printing and reproduction of recorded media
Wearing apparel; dressing and dyeing of fur
Leather; manufacture of luggage, handbags, footwear
Textiles
Rubber and plastics products
Motor vehicles, trailers and semi-trailers
Other non-metallic mineral products
Mining of metal ores
Food products and beverages
Basic metals
Tobacco products
Paper and paper products
Wood and products of wood, except furniture
Coke, refined petroleum products and nuclear fuel
0.994
0.901
0.777
0.675
0.675
0.656
0.637
0.604
0.540
0.466
0.327
0.232
0.185
0.165
0.119
0.117
0.103
0.083
0.082
0.073
0.065
0.058
0.018
0.002
-2.813
-3.255
-2.764
-1.962
-1.962
-1.236
-1.944
-1.966
-0.436
-1.066
-1.357
-2.296
-2.003
-0.981
-0.784
-1.586
1.281
2.422
0.292
-0.244
-1.203
0.307
0.278
1.472
Notes: Airi and Heavyi stand for air share and heaviness of industry-level imports into the UK in 2005. Precisely, air
share is imports by air divided by total imports by air and vessel. Heaviness is the natural logarithm of the weight/value
ratio of imports by vessel.
30
Table 7: Transport Intensity: Intensive Margin
∆ ln(RCpg ) × Θi
∆ ln(RCpg ) × Airi
(1)
∆ln(tradefpgi )
(2)
∆ln(tradefpgi )
(3)
∆ln(tradefpgi )
(4)
∆ln(tradefpgi )
-0.676∗∗∗
(0.175)
1.095∗∗
(0.463)
-0.682∗∗∗
(0.182)
-0.536∗∗∗
(0.181)
1.700∗∗∗
(0.538)
0.302∗
(0.160)
-0.648∗∗∗
(0.207)
∆ ln(RCpg ) × Heavyi
0.0307
(0.138)
∆ ln(RCpg ) × T SiHS
Regression
Fixed Effects
Observations
R2
IV
p-g-f
5,299
0.007
IV
p-g-f
5,299
0.005
IV
p-g-f
5,299
0.008
30.97∗∗
(12.93)
IV
p-g-f
4,534
0.006
Notes: Airi and Heavyi stand for air share and heaviness of industry-level imports into the UK in 2005. Precisely,
air share is imports by air divided by the sum of imports by air and vessel. Heaviness is the natural logarithm of the
weight/value ratio of imports by vessel. θi denotes the demand elasticity of industry i as estimated by Broda and Weinstein (2006). T SiHS is the baseline time-sensitivity measure of industry i estimated by Hummels and Schaur (2013).
Standard errors in parentheses are clustered at the pg level. Significance: * 10 percent, ** 5 percent, *** 1 percent.
Table 8: Transport Intensity: Extensive Margin
∆ ln(RCpg ) × Θi
∆ ln(RCpg ) × Airi
(1)
f
N ewpgi
(2)
f
N ewpgi
(3)
f
N ewpgi
-0.026
(0.029)
0.144∗
(0.082)
-0.030
(0.029)
-0.023
(0.030)
0.165∗
(0.091)
0.010
(0.030)
IV
p-g-f,i
12,203
0.056
∆ ln(RCpg ) × Heavyi
Regression
Fixed Effects
Observations
R2
IV
p-g-f,i
12,203
0.055
-0.015
(0.027)
IV
p-g-f,i
12,203
0.055
ost
re
Notes: N ewpg is equal to P r(tradeP
> 0&tradeP
pgi
pgi = 0). Airi and Heavyi stand for air share and heaviness of
industry-level imports into the UK in 2005. Precisely, air share is imports by air divided by total imports by air and vessel. Heaviness is the natural logarithm of the weight/value ratio of imports by vessel. θi denotes the demand elasticity
of industry i as estimated by Broda and Weinstein (2006). Standard errors in parentheses are clustered at the pg level.
Significance: * 10 percent, ** 5 percent, *** 1 percent.
31