(derivadas Trigonometricas).

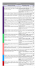
REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR DE LA DEFENSA
UNIVERSIDAD NACIONAL EXPERIMENTAL DE LA FUERZA ARMADA NACIONAL
NUCLEO- GUANARE
GUIA 4 (Derivada Trigonométricas-Orden S.-Implicitas)
I. Derivada de Funciones Trigonométricas
La derivación de las funciones trigonométricas es el proceso matemático de
encontrar el ritmo al cual una función trigonométrica cambia respecto de la
variable independiente; es decir, la derivada de la función.
1 Cal cula la derivada de la funciones trigonométricas:
1
2
3
4
5
6
7
8
9
2 Cal cula la derivada de la funciones trigonométricas inversas:
1
2
3
4
5
1
Prof. REIMY PALENCIA……………reimypalencia.webnode.com.ve
3 Deri var por la regla de la cadena las funciones:
1
2
3
4
5
6
7
Ejemplos para discusión: Halla la derivada de:
1) y = 3 sen x
2) y = x + cos x
4) y = x - tan x
5) y = x sec x
7) y = 7 cos x -sec2 x
8) y= 2 tan x sec2 x
10) y = sec2 x – cos 4x
9) y = 3 sen2 x cos x
12) y’ = -4 csc2 2x cot 2x
11) y’ = 8 sen 4x cos 4x
13) y = sec2 x + csc x cot x 14) y’ = 1 + cos x
d
csc 4 x 3 2 x 4
dx
1
csc 4 x 3 2 x 4
2
12 x 2 2 csc 4 x 3
d
csc 4 x 3 2 x 4
dx
1
2
d
csc 4 x 3 2 x 4
dx
2 x 4 cot 4 x 3 2 x 4
2 csc 4 x 3
6x
2
1
csc 4 x
3
2x 4
2 x 4 cot 4 x
csc 4 x
2
15) y’ = x cos x + sen x
3
2x 4
csc 4 x 3 2 x 4 cot 4 x 3
12 x 2 2
3
2x 4
d
4x3 2x 4
dx
d
2x 4
4x3 2x 4
dx
csc 4 x 3 2 x 4 cot 4 x 3 2 x 4
3
csc 4 x 3 2 x 4 cot 4 x 3 2 x 4
2 4x 2x 4
6x 2 1
csc 4 x 3 2 x 4 cot 4 x 3 2 x 4
3
4x 2x 4
Prof. REIMY PALENCIA……………reimypalencia.webnode.com.ve
II. DERIVADAS DE ORDEN SUPERIOR
Una derivada de orden superior es aquella derivada que resulta de formar una
nueva función a partir de una primera derivada, es decir, si se tiene una
función f que es derivable, se puede formar una nueva función que se denota
por f´ y se lee primera derivada de f, y así sucesivamente se pueden ir formando
derivadas a partir de la anterior y se nombran segunda, tercera derivada de f, etc.
Ejercicios: Obtenga la quinta derivada de las siguientes funciones.
1.
2.
3.
4.
5.
III. Derivación de funciones implícitas
Una función real de variable real es implícita cuando en su regla de
correspondencia ninguna variable está despejada en términos de la otra. La
derivada de una función implícita se puede determinar con respecto a la
variable independiente x o con respecto a la variable dependiente y mediante
el proceso denominado derivación implícita. Al derivar funciones implícitas, es
común aplicar la regla de la cadena. El procedimiento para esta derivación se
puede consultar en el libro de texto y en el formulario o prontuario.
3
Prof. REIMY PALENCIA……………reimypalencia.webnode.com.ve
Ejemplo: Mediante derivación implícita, obtenga la derivada con respecto a x
de la función
Derivando con respecto a x
)=
Aquí se debe tener en cuenta que para derivar los términos
y
se debe aplicar el teorema de la derivada de un producto.
Calculando las derivadas y representando por y ´
respecto a x.
la derivada de y con
Reordenando y como se desea obtener el valor de y´, los términos que
contiene a y´ se agrupan en el primer miembro, factorizando los términos
Despejando y’, se tiene la derivada de la función con respecto a x.
Ejercicios: Derive implícitamente con respecto a x las siguientes funciones
1.
X4 y3 + 5x2 = 8
2.
3.
5.
Y7 + x = 6
6.
Xy2 – 6x = y
7.
4.
4
Prof. REIMY PALENCIA……………reimypalencia.webnode.com.ve
T + x -6y5 = y