document-reponse dr1

http://al9ahira.com/
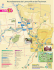
Itinéraire d'accès à Al9ahira (point B sur la carte) en partant de la Place Ibéria
CONCOURSNATIONALCOMMUN
FILIERES:MP&PSI
SESSION:2014
EPREUVEDESCIENCESINDUSTRIELLESPOURL’INGENIEUR
ELEMENTSDECORRECTION
ROBOTDETRAITEAUTOMATIQUEASTRONAUTA3
3.Etudefonctionnellepartielleexterneetimplantationdurobot
Question1:Recopieretcomplétersurvotrecopiel’actigrammeA‐0incompletdurobotdetraite
AstronautA3donnésurlafigure5suivante.
Energie NourritureCodevache
Vachetraite
Traireautomatiquementune
vacheetluifournirunequantité
Vache
denourritureadaptée.
Lait
A‐0
RobotdetraiteAstronautA3
Figure5:SADTincompletdeniveauA‐0durobotdetraieAstronautA3.
Question2:CompléterlediagrammeFASTpartieldurobotdetraiteAstronautA3,donnésurlafigure
R1dudocumentréponseDR1.
VoirdocumentréponseDR1.
4.EtudedelafonctionFT10:«Gérerlatraite»
Question3:Déterminerlenombredetraitesquepeuteffectuerlerobotsuruneplaged’utilisationde20
heures. En déduire la taille maximale du troupeau (nombre maximum de vaches) lors de
l’implantationd’unrobotAstronautA3.




5traitesprennent:5x6+4=34min
20traitesprennent:3x(34)+5x6+9=141min
En20h,onpeutréaliser:20x60/141=8fois20traitesilreste72minquipermettentde
réaliser10traitessoit170traitesen20heures.
Letroupeaupeutdonccontenir170/2,5=68vaches.
Question4:
On demande de compléter le nouveau grafcet G1 de gestion des tâches fourni sur la figure R2 du
document‐réponseDR2,desorteàprendreenconsidération:
‐ Lestâchespouvants’effectuersimultanément,plusparticulièrement,aprèsquelecyclederinçage
trayons soit terminé, on peut simultanément continuer le cycle par rinçage des canalisations, la
transmissiondedonnéesetleplacementdubrasenpositionattente,toutenouvrantlaportede
sortiepourlibérerlavachepuislarefermeretouvrircelledel’entrée.
SciencesIndustriellespourl’Ingénieur
1/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
‐ Le cas où l’intervalle entre deux traites est insuffisant et qu’alors la traite est non autorisée: la
portedesorties’ouvre,alors,libérantlavache.Dèssasortiedubox,laportedesortiesefermeet
celled’entrées’ouvre.
VoirDocument‐réponseDR2
5.EtudedelafonctionFT122«Peserlavache»
Question5: a) Ecrireleséquationsissuesdel’applicationduprincipefondamentaldelastatiqueà
l’ensembleE=(plateau+vache)aupointM.
b) DéduirelepoidsPdelavacheetlescoordonnéesXGetYGdesoncentredegravitéG,en
fonctiondesdonnées,faireensuitel’applicationnumérique.
a) PFSappliquéàl’ensembleE=(plateaupeseur+vache):
{T (E  E )} = {TM (B  Plat .)} + {TN ( B  Plat .)} +{TK (B  Plat .)} + {T (Pes.  Vache )} = {0} ïìï 0 0ïüï
ïìï 0
ïï
ïï
ï
{TM ( B  Plat .)} = í 0 0ý , {TN ( B  Plat .)} = ïí 0
ïï
ï
ïï
ïïZ M 0ïïþïR
ïîïZ N
Mî
N
0

TRSprojetésur z : Z K + Z M + Z N - P = 0 
 
 
 
TMSenM: MN  Z N .z + MK  Z K .z - MG  P .z = 0 
0üïï
ïìï 0
ïï
ï
0ý et {TK ( B  Plat .)} = ïí 0
ï
ïï
0ïïþïR
ïîïZ K
K
0
0ü
ï
ï
ï
0ï
ý
ï
0ï
ï
ïR0
þ


 b 




 
b. y  Z N .z + (a.x + . y )  Z K .z -( X G .x + YG . y + h.z )  P .z = 0 2


 b


 
b.Z N . x - a.Z K . y + .Z K . x + X G .P . y -YG .P . x = 0 2

é
ù 
 
b
êb.Z N + .Z K -YG .P ú .x + [-a.Z K + X G .P ]. y = 0 êë
úû
2
b
D’où: b.Z N + .Z K -YG .P = 0 et -a.Z K + X G .P = 0 2
c) P = Z K + Z M + Z N AN: P = 600 daN XG =
a.Z K
a.Z K
=
AN: X G = 0,44 m P
ZK + ZM + ZN
YG =
b.Z N b.Z K
2b.Z N + b.Z K
+
=
AN: YG = 1,5 m P
2P
2( Z K + Z M + Z N )
6.EtudedelafonctionFT131:«Mettreenpositionlesorganesnécessairesàlatraite»
6.1.Etudehyperstatique
Question6: a) Dresserlegraphedeliaisonsdubrasderobot.
b) Donner,enspécifiantlesmouvementsconcernés,lesmobilitésutileetinternedu
système.
c) Calculerledegréd’hypersatismehdusystème.Quelleestl’influencedecettevaleurde
hsurlaréalisationdusysème?
d) Danslecasoùlemécanismeesthyperstatique,proposerunesolutionpourlerendre
isostatiquesachantqueseuleslesliaisonsenD,E,FetHpeuventêtremodifiées.
SciencesIndustriellespourl’Ingénieur
2/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
a) Legraphedeliaisonsdubrasderobot:
Pivotglissant 51

d’axe ( D , y5 )
Pivotd’axe
Pivotd’axe


(F , x0 ) ( D , x0 ) 50
0
Pivotd’axe

( A , x0 ) Pivotd’axe

( H , x0 ) Pivotglissant

60
d’axe (E , y6 )
61
2
Pivotd’axe

( B , x0 ) Pivotd’axe

(E , x0 ) 3+4
b) Mobilité:m=mu+mi
Mobilitéutile:mu=2(lesmouvementsdetranslationdesdeuxvérinsV5etV6).
Mobilitéinterne:mi=0.
c) Degréd’hyperstatisme: h = m + E c – Ic = 2 + 6 x 2 ‐10 = 4 .
Influencedeh:systèmerigidemaisnécéssite4contraintesdimensionnelleset/ou
géomètriquesàrespecterlorsdesaréalisationpourquelesystèmepuisseêtremontéet
fonctionner.
d) Solutionisostatique:
OnremplacelesliaisonsenD,E,FetHpardesliaisonssphériques.Eneffet:
midevient4,doncm=6et h = m + E c – Ic = 6 + 6 x 2–18 = 0 ,onobtientainsiunsystème
isostatique.
6.2.Etudecinématique

Question7: a) Représenter,àl’échelleproposée,levecteurvitesse V ( D Î 51 /50) .

b) ParcompositiondesvitessesenD,déterminerlesvecteursvitesses V ( D Î 50 /0) et

V ( D Î 2/ 0) .

c) Déterminerlevecteurvitesse V ( B Î 2/0) .

d) Déterminerladirectionduvecteurvitesse V (E Î 3/ 0) .
e) DéterminerlecentreinstantannéderotationI30dumouvementde(3)parrapportà(0).

f) Déterminerlevecteurvitesse V (G4 Î 4 /0) ,donnersanorme.

a) V ( D Î 51 /50) estportéeparFD,voirDR3
b) ParcompositiondesvitessesenD:




V ( D Î 2/ 0) =. V ( D Î 2/51) + V ( D Î 51 /50) + V ( D Î 50 /0) 
V ( D Î 2/ 0) ^(AD)carAºCIRdumouvementde1/0.

V ( D Î 51 /50) déjàtracée

V ( D Î 50 /0) ^(FD)carFºCIRdumouvementde50/0.


Entraçantleparallélogrammeondéterminecomplétementlesvitesses V ( D Î 50 / 0) et V ( D Î 2/ 0) .

c) Vecteurvitesse V ( B Î 2/ 0) .

V ( B Î 2/0) ^(AB)carAºCIRdumouvementde1/0.
SciencesIndustriellespourl’Ingénieur
3/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection

Lavitessevarielinéairementlelongde(ADE),d’où V ( B Î 2/0) .
Session2014

d) Directionduvecteurvitesse V (E Î 3/ 0) .



V (E Î 3/ 0) = V (E Î 3/ 6) + V (E Î 6 / 0) ^(HE)carHºCIRdumouvementde6/0.
e) CentreinstantannéderotationI30dumouvementde(3)parrapportà(0).



Ona: V ( B Î 3/ 0) = V ( B Î 3/2) + V ( B Î 2/ 0) 

I30=(^ V ( B Î 3/ 0) )Ç(^ V (E Î 3/ 0) )c.à.d.I30=(AB)Ç(HE).
Oubienenfaisantusageduthéorèmedes3plansglissants:I30=(I32I20)Ç(I36I60)c.à.d.I30=(BA)Ç(EH)

f) Vecteurvitesse V (G4 Î 4 /0) 
V (G4 Î 4 / 0) ^ ( I30G4 ) 

SoitJlepointde ( I30 B ) telque:I30B’=I30G4,alors: V (G4 Î 4 / 0) = V ( J Î 3/ 0) ;


Lavitessevarielinéairementlelongde(I30JB),d’où: V ( J Î 3/ 0) et V (G4 Î 4 /0) .
6.3.Etudeduguidageentranslationduchariot1
Question8: a) EnseplaçantàlalimitedeglissementetenappliquantlesloisdeCoulomb,tracer,en
justifiant,lessupportsdesactionsmécaniquesdubâti(0)surl’ensemble(E)enMetN.
b) DéterminergraphiquementlapositionlimiteLlim dupointKquiassurel’équilibrestrict
(limite)del’ensembleE.
c) Al’aided’uneanalysegéométrique,déterminerLlimenfonctiondefetdesdonnées.
d) Donner la condition sur la distance L pour éviter tout risque de coincement (arc‐
boutement)duchariot1parrapportaubâti(0).Justifier.
a) Enseplaçantàlalimitedeglissement(ouàl’équilibrestrict),lesloisdeCoulombdisentqueles


supportsdesactionsmécaniques RM et RN dubâti(0)surl’ensemble(E)enMetNfontl’angle

javecleursnormalesdecontactenMetNdesortequeleurscomposantestangentielles TM et


TN soientopposéesauxvitessesdeglissementenMetN(respectivement)portéespar(+ x0 ).
Leseffortsnormauxétantdirigésverslamatièredel’ensembleE.
 

b) L’équilibreestassurésilestroisforces RM , RN et F auxquellesestsoumisl’ensemble(E)sont

concourants(etqueleursommevectorielleestnulle).L’intersectiondesactions RM et

RN définitlapositionlimiteLlim.
æ
æ
h
eö
eö
c) Ona: h = çççLlim + ÷÷÷ tan j + çççLlim - ÷÷÷ tan j = 2Llim tan j = 2Llim f  Llim =
è
ø
è
ø
2f
2
2
d) Pourévitertoutrisquedecoincement(arc‐boutement)duchariot1parrapportaubâti(0)il
faudraqueL<Llim.Eneffet,pourqu’ilyaitcoincement(c.à.d.équilibre)ilfaudraqueles3forces
appliquéesà(E)soientconcourantescommec’estdéjàditetpourquececipuissesefaireilfaut
 
quelesactions RM , RN fassentunanglesupérieuràjavecleursnormalesdecontactenMetN
(horscônedefrottement)chosequiestimpossibled’aprèslesloisdeCoulomb.
SciencesIndustriellespourl’Ingénieur
4/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
6.4.Dimensionnementdesactionneurs

Question9: a) Déterminerlescomposantesduvecteurposition BG ducentred’inertieG3dubras3.
3
b) Donner, en justifiant, la forme simplifiée de la matrice d’inertie I (B,3) dans la base
  
( x0 , y3 , z3 ) .
  
c) Exprimer en fonction des données, et dans la base ( x0 , y3 , z3 ) , la matrice d’inertie
  
I (G31 ,31) .Endéduirelamatriced'inertie I (B,31) danslabase ( x0 , y3 , z3 ) .
  
d) Exprimer en fonction des données, et dans la base ( x0 , y3 , z3 ) , les matrices d'inertie
I (G32 ,32) et I (G33 ,33) .Endéduirelesmatricesd'inertie I ( B ,32) et I ( B ,33) .
  
e) Déduirel'expressiondelamatriced’inertie I (B,3) danslabase ( x0 , y3 , z3 ) .
a) lescomposantes X G 3 ,YG 3 et Z G 3 ducentred’inertieG3dubras3.




BG3 = X G 3 . x0 + YG3 . y3 + Z G 3 .z3



1
=
.(m31 BG31 + m32 BG32 + m33 BG33 )
(m31 + 2m32 )
=
ì
æa  h  b  ö
æ a  h  bö  ü
ï
ï
1
b
.ï
í-m31 z3 + m32 ççç x0 - y3 - z3 ÷÷÷ + m33 ççç- x0 - y3 - ÷÷÷ z3 ï
ý
ï
è
ø
è
ø
(m31 + 2m32 ) î
2
2
2
2
2
2
2 ï
ï
ï
þ
{
}
= -


1
b
⋅ m31 z3 + m32 (hy3 + bz3 )
(m31 + 2m32 )
2
= -


1
⋅ {(m31 / 2 + m32 ) bz3 + m32hy3 }
(m31 + 2m32 )
D’où; X G3 = 0;YG3 = -

 b 
m
BG3 =- 32 .h. y3 - .z3 2
m3
m32h
b
;Z G 3 = - 2
m3
b) Formesimplifiéedelamatriced’inertie I ( B ,3) .
 
Lagéométriedubrasintermédiaire3présenteunplandesymétrie ( B , y3 , z3 ) ,donc:
æ A3
0
0ö÷
çç
÷
I( B ,3) = çç 0
B3 -D3 ÷÷÷
çç
÷÷
çè 0 -D3
C3 ÷ø( x , y , z )
0 3 3
c) Matriced’inertie I (G31 ,31) et I ( B ,31) æb2
ç
m31 çç
I(G31 ,31) =
ç0
12 ççç
çè 0
0
2
a + b2
0
0 ö÷
÷÷
0 ÷÷
÷÷
a2 ÷÷ø 
;
 
( x0 , y3 , z3 )
D’aprèsHuygensona: I( B ,31) = I (G31 ,31) + I ( B , {G31 , m31 }) 2
æ
0
0÷ö
ççm31b / 4
÷÷

b
ç
0
m31b2 / 4 0÷÷
Etpuisque: BG31 = - z3 ,alors: I( B , {G31 , m31 }) =çç
÷÷
çç
2
0
0
0÷÷ø   
çè
( x0 , y3 , z3 )
SciencesIndustriellespourl’Ingénieur
5/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
2
æ
ççm b
çç 31 3
çç
ç
D’où: I( B ,31) = ççç 0
çç
çç
çç 0
è
Elémentsdecorrection
0
æ a2 b2 ö
m31 ççç + ÷÷÷
è 12 3 ÷ø
0
ö÷
÷÷
÷÷
÷÷
0 ÷÷÷
÷÷
÷
2÷
a ÷÷
m31 ÷÷
12 ø 
Session2014
0
 
( x0 , y3 , z3 )
d) Matricesd’inertie: I (G32 ,32) , I (G33 ,33) , I ( B ,32) et I ( B ,33) .
2
æ 2
ççh + b
m
I(G32 ,32) = I(G33 ,33) = 32 ççç 0
12 çç
çè 0
0
b2
0
0 ö÷
÷÷
0 ÷÷
÷÷
h2 ÷÷ø 
 
( x0 , y3 , z3 )








Ona: BG32 = a /2. x0 - h / 2. y3 - b /2.z3 et BG32 = -a /2. x0 - h / 2. y3 - b / 2.z3 Donc:
æ m32 2
ö÷
m
ah
ab
çç
(h + b2 ) + 32 (h2 + b2 )
m32
m32
÷÷
çç 12
÷÷
4
4
4
çç
÷÷
m32 2 m32 2
ah
bh
÷÷
çç
2
(
)
I( B ,32) = ç
m32
b +
a +b
-m32
÷÷
çç
4
12
4
4
÷÷
çç
÷÷
m32 2 m32 2
ab
bh
(a + h2 )÷÷÷
m32
h +
-m32
ççç
è
ø( x0 , y3 , z3 )
4
4
12
4
æ m32 2
ah
ab ö÷
çç
(h + b2 )
m32
m32
÷÷
çç 3
÷÷
4
4
çç
÷
2
2
æa
çç
ah
b ö÷
bh ÷÷÷
ç
 I( B ,32) = ç m32
m32 çç + ÷÷
-m32
÷
è4
4
3ø
4 ÷÷÷
ççç
÷
çç
æ a2 h2 ö÷÷÷÷
bh
çç m ab
ç
m32 çç + ÷÷÷÷÷
-m32
32
çè
è4
4
4
3 øø( x0 , y3 , z3 )
æ m33 2
ah
ab ö÷
çç
(h + b2 )
-m33
-m33
÷
çç 3
4
4 ÷÷÷
çç
÷
æ a2 b2 ö÷
çç
ah
bh ÷÷÷
ç
Demême: I( B ,33) = ç -m33
m33 çç + ÷÷
-m33
÷
çç
è4
4
3ø
4 ÷÷÷
çç
÷
æ a2 h2 ö÷÷÷÷
çç
ab
bh
ç
ç -m33
m33 çç + ÷÷÷÷÷
-m33
çè
è4
4
4
3 øø( x0 , y3 , z3 )
e) Matriced’inertie I ( B ,3) I( B ,3) = I ( B ,31) + I( B ,32) + I ( B ,33) æ A3
0
0ö÷
çç
÷
ç
I( B ,3) = ç 0
B3 -D3 ÷÷÷
çç
÷÷
çè 0 -D3
C3 ÷ø( x , y , z )
0 3 3
SciencesIndustriellespourl’Ingénieur
6/20
http://al9ahira.com
TournezlapageS.V.P.
http://al9ahira.com
ConcoursNationalCommun
Elémentsdecorrection
ì
ï
b2 m32 + m33 2
ï
A
=
m
+
(h + b2 )
ï 3
31
ï
3
3
ï
avec: í
ï
æ a2 h2 ö
ï
a2
ï
C3 = m31 + (m32 + m33 )ççç + ÷÷÷ ;
ï
ï
è4
12
3ø
ï
î
Session2014
æ a2 b2 ö
æ a2 b2 ö
B3 = m31 çç + ÷÷÷ + (m32 + m33 )ççç + ÷÷÷
è4
çè 12 3 ø÷
3ø
;
bh
D3 = (m32 + m33 )
4
Question10: a) Déterminerletorseurcinétique,aupointB,dubras(3)danssonmouvement/àR0.

b) Déterminer la projection sur x0 des éléments de réduction du torseur cinétique, au
pointB,delatête(4)danssonmouvement/àR0.
a) Torseurcinétique,aupointB,dubras(3)danssonmouvement/àR0.

ì
ï
ï
Rc ( S3 / R0 ) ü
ï
ï
{C( S3 / R0 )} = í 
ý
ï
ï
(
B
,
S
/
R
)
s
ï
ï
3
0 þ
Bî


æ 

 ö
L
Rc ( S3 / R0 ) = m3V (G3 Î S3 / R0 ) = m3 ççç x .x0 + L2 .q2 .z2 + 3 (q2 + q3 ). y3 ÷÷÷
è
ø
2
 


s( B , S3 / R0 ) = m3 .BG3  V ( B Î S3 / R0 ) + I ( B ,3).W(3/0)



L3 
= -m3 z3  ( x .x0 + L2q2 z2 ) + A3 (q2 + q3 )x0
2



m .L
= - 3 3 ( x . y3 - L2q2 sin q3 x0 ) + A3 (q2 + q3 )x0
2


é
= ë A3 (q2 + q3 ) + 12 m3 L3 L2q2 sin q3 ùû .x0 - 12 m3 L3 x . y3
b) Torseurcinétique,aupointB,delatête(4)danssonmouvement/àR0.

ì R (S / R ) ï
ü
ï
ï
{C( S 4 / R0 )} = í  c 4 0 ïý
ïs( B , S 4 / R0 )ï
ï
î
þ
Bï

 

x0 .Rc ( S 4 / R0 ) = x0 .m4V (G4 Î S 4 / R0 ) = m4 .x

 
 
 
x0 .s( B , S 4 / R0 ) = x0 .s(G4 , S3 / R0 ) + x0 . BG4  m4V (G4 Î S 4 / R0 )




= A4 (q2 + q3 )- m4 ( x0  (L3 z3 + L4 y3 )) .V (G4 Î S 4 / R0 )






= A4 (q2 + q3 )- m4 (L4 z3 - L3 y3 ) .( x .x0 + L2 .q2 .z2 + L3 (q2 + q3 ). y3 - L4 (q2 + q3 ).z3 )
)
(
= éê A4 (q2 + q3 ) + m4 ((L32 + L42 )(q2 + q3 ) + L2 .q2 .(L3 sin q3 - L4 cos q3 ))ùú
ë
û
Ondonneleschémad’analysedusystèmesurlafigure9suivante:
V1
0
Onrappellequetoutesles
liaisonssontavecfrottement
visqueuxetquelesmassesdes
vérinssontnégligées
Glissièrede

direction x0 1
Pivotd’axe

( A , x0 ) V6
V5
Figure9:Schémad’analysedusystème
SciencesIndustriellespourl’Ingénieur
Vache
7/20
3+4
2
Pesanteur
Pivotd’axe

( B , x0 ) http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
Les lois de mouvement étant connues on désire dimensionner les vérins V1, V5 et V6 permettant de
réalisercesloisdemouvement.
Question11: Sansdévelopperlestermesdynamiques,écrireleséquationspermettantdedéterminerles
actions mécaniques des vérins: F1, F5 et F6. Indiquer, clairement, le(s) système(s) à isoler,
le(s)théorème(s)àutiliser.
DéterminationdeF1:Onisolel’ensembleE1=(S1+S2+S3+S4),
{E1  E1 } = {
V1  S1 } + {Vache  S1 } + {S 0  S1 }




R (V1  S1 ). x0 =F1


R (Vache  S1 ). x0 =-Fp


R ( S0  S1 ). x0 =- f01 . x
+ {Pes .  E1 } 


R ( Pes . E1 ). x0 =0

TRDenprojectionsur x0 :
 
x0 .RD (E1 / R0 ) = F1 - Fp - f01 .x
 
F1 = x0 .RD (E1 / R0 ) + Fp + f01 .x
DéterminationdeF6:
 Onisolel’ensembleE2=(S3+S4)
{E2  E2 } = {
S 2  S3 }


MB ( S2  S3 ). x0 =- f23 . q3
+ {V6  S3 } + {Pes.  E2 } 

ïìïF6 y6 ïüï
í  ý
ï 0 ïï
þ
ï
Eî

TMDaupointBenprojectionsur x0 :
 
 
 
 


x0 .d ( B , E2 / R0 ) = x0 . BE  F6 . y6 - BG3  m3 . g.z0 -( BC + CG4 )  m4 . g.z0 - f23 .q3 )
(
 
L
x0 .d ( B , E2 / R0 ) = a3F6 cos(q6 - q2 - q3 )- m3 g 3 sin(q2 + q3 ) + m4 g (-L3 sin(q2 + q3 ) + L4 cos(q2 + q3 ))- f23 .q3
2
æm
ö
 
x0 .d ( B , E2 / R0 ) + ççç 3 + m4 ÷÷÷ gL3 s in(q2 + q3 )- m4 gL4 cos(q2 + q3 ) + f23 .q3
è2
ø
F6 =
a3 cos(q6 - q2 - q3 )
DéterminationdeF5:
Onisolel’ensembleE3=(S2+S3+S4)
{E3  E3 } = {
S1  S 2 }


M A ( S1  S2 ). x0 =- f12 .q2
+ {V5  S 2 } + {V6  S 3 } + {Pes .  E3 } 



ïìïF5 y5 üïï
í  ý
ïï 0 þïï
Dî
ïìïF6 y6 üïï
í  ý
ïï 0 þïï
Eî

TMDaupointAenprojectionsur x0 :

 
 

 
 
 

x0 .d ( A, E3 / R0 )= x0 . AD  F5 . y5 + AE  F6 . y6 - AG2  m2 . g.z0 - AG3  m3 . g.z0 - AG4  m4 . g.z0 - f12 .q2
)
(
æ
ö
 
L
L
x0 .d ( A, E3 / R0 )= a2F5 sin(q5 - q2 ) + h6 F6 cos q5 - f21q2 - m2 g 2 cos q2 - m3 g ççL2 cos q2 + 3 sin(q2 + q3 )÷÷÷
çè
ø
2
2
-m4 . g.(L2 cos q2 + L3 sin(q2 + q3 )- L4 cos(q2 + q3 ))
æm
ö
æm
ö
 
x0 .d ( A, E3 / R0 ) - h6 F6 cos q5 + f21q2 + çç 2 + m3 + m4 ÷÷÷ gL2 cos q2 + çç 3 + m4 ÷÷÷ gL3 sin(q2 + q3 ) + m4 gL4 cos(q2 + q3 )
è2
ø
è2
ø
F5 =
a2 sin(q5 - q2 )
SciencesIndustriellespourl’Ingénieur
8/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
Question12:Encalculantlestermesdynamiques,déterminercomplétementF1etF6enfonctiondes
données.
DéterminationcomplètedeF1:
 
 
 
 
d  
d  
x0 .RD (E1 / R0 ) = ( x0 .RC (E1 / R0 )) = ( x0 .RC ( S1 / R0 ) + x 0 .RC ( S 2 / R0 ) + x 0 .RC ( S 3 / R0 ) + x0 .RC ( S 4 / R0 ))
dt
dt
= (m1 + m2 + m3 + m4 ).x
F1 = (m1 + m2 + m3 + m4 ) x + f01 .x + Fp DéterminationcomplètedeF6:
æm
ö
 
x0 .d ( B , E2 / R0 ) + ççç 3 + m4 ÷÷÷ gL3 s in(q2 + q3 )- m4 gL4 cos(q2 + q3 ) + f23 .q3
è2
ø
F6 =
a3 cos(q6 - q2 - q3 )
Avec:





 æ ds( B , E2 / R0 )ö÷

x0 .d ( B , E2 / R0 ) = x0 .ççç
÷÷ + x0 .(mE 2V ( B / R0 )  V (GE 2 / R0 ))
è
øR0
dt



 
d 
= (s( B , E2 / R0 ).x0 ) + ( x0  V ( B / R0 )) .(m3V (G3 Î S3 / R0 ) + m4V (G4 Î S 4 / R0 )
dt
 





d 
x0 .d ( B , E2 / R0 ) = (s( B , E2 / R0 ).x0 ) + ( x0  L2 .q2 .z2 ) .(m3V (G3 Î S3 / R0 ) + m4V (G4 Î S 4 / R0 )
dt
æ æ 
ççm çç x .x + L .q .z + L3 (q + q ). y ö÷÷ +


d 
3
0
2 2 2
2
3
3÷
ø
2
= (s( B , E2 / R0 ).x0 ) - L2 .q2 . y2 .ççç çè
dt




çç
èçm ( x .x + L .q .z + L (q + q ). y - L (q + q ).z
4
0
2
2
2
3
2
3
3
4
2
3
ö÷
÷÷
÷÷
÷÷ ÷
)
3 ø

d 
= (s( B , E2 / R0 ).x0 ) - L2q2 (q2 + q3 )( 12 m3 L3 cos q3 + m4 (L3 cos q3 + L4 sin q3 ))
dt






s( B , E2 / R0 ).x0 = s( B , S3 / R0 ).x0 + s( B , S 4 / R0 ).x0
= éëê( A3 + 12 m3 L23 )(q2 + q3 ) + 12 m3 L3 L2q2 sin q3 ùûú +
é A (q + q ) + m ((L 2 + L 2 )(q + q ) + L .q .(L sin q - L cos q ))ù
3
4
3
4
2
3
2 2
3
3
4
3 ûú
ëê 4 2
 
x0 .d ( B , E2 / R0 ) = ( A3 + A4 + 12 m3 L23 + m4 ( L23 + L24 ))(q2 + q3 ) + ëé 12 m3 L3 sin q3 + m4 (L3 sin q3 - L4 cos q3 )ûù L2q2
-( 12 m3 L3 cos q3 + m4 L2 (L3 cos q3 + L4 sin q3 )) L2q22
7.EtudedelafonctionFT135:«Réguleretasservirlapositiondesorganesdetraite»
Lecahierdeschargespartieldécrivantlesperformancesassociéesauchariot1estlesuivant:
Fonction
FT135
Critères
Niveauxetéventuelleflexibilité
AxeN°1(translationduchariot1parrapportaubâti)
Stabilitédel’axe
Margedephase:MP³45°
Amortissementdel’axe Aucundépassementtransitoirepermis
‐ Insensibilitéàuneperturbationimpulsion.
Précisionde
‐ Ecartstatique(écartenrégimepermanentsuiteàun
positionnementdel’axe
échelondeposition)nul.
Rapiditédel’axe
Pulsationdecoupureà0dB(oudegainunité):wc0=10rad.s‐1
SciencesIndustriellespourl’Ingénieur
9/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
7.1.Modélisationdessystèmesélectro‐hydrauliques
Question13: Ensupposantlesconditionsinitialesnulles,écrireleséquations(1),(2),(3)et(4)dansle
domainedeLaplace,puisrecopieretcompléterleschéma‐blocsdelafigure11.
(1): q(t ) = K D .u(t )  Q( p) = K D .U( p) .(2)qfuite(t)= l( Pa (t )- Pb (t )) Qfuite(t)= l( Pa ( p)- Pb ( p)) (3) : q(t ) = S .v(t ) +
(4) : Méq
s dDP(t )
s
⋅
+ lDP(t )  Q( p) = S.V ( p) +
p.DP( p) + l.DP( p) .
2b
2b
dt
dv(t )
= S .DP(t )- f .v(t )- Fp (t )  M éq .p.V ( p) = S.DP( p) - f .V ( p) - Fp ( p) . dt
Qfuite(p)
l
Fp(p)
U(p)
KD Q(p) 



2b
sp
P(p)


S
1
f + Méq .p
V(p)
S
Figure11:Schéma‐blocdel’ensemble«vérin+charge»
Question14: a) Ecrirelafonctiondetransfert
Ku
V ( p)
où
pour Fp ( p) = 0 souslaforme
1 + Ap + Bp2
U( p)
lestermesA,BetKuserontexplicités.
b) Écrirelafonctiondetransfert
K f (1 + t p)
V ( p)
pour U( p) = 0 souslaforme
où
Fp ( p)
1 + Ap + Bp2
lestermestetKfserontexplicités.

c) Montrerquelemodèlecompletassociéàl’axe x0 peutsemettresouslaformedu
schémafonctionneldonnéfigure12oùlestermesF(p),G(p)etH(p)serontexplicités.
a) Fonctiondetransfert
V ( p)
pour Fp ( p) = 0 U( p)
2b
1
⋅S ⋅
f + Méq p
2bl + s p
V ( p)
2BS
= KD.
= KD .
b
2
1
U( p) Fp ( p )=0
(2bl + s p)( f + Méq p) + 2b S 2
⋅S2 ⋅
1+
f + Méq p
2Bl + s p
2b S
= KD.
=
2
2bl f + 2b S + (2blMéq + s f )p + sMéq p2
=
avec : Ku = K D .
2b S
2b(l f + S 2 )
sMéq
2blMéq + s f
2
p+
p
1+
2b(l f + S 2 )
2b(l f + S 2 )
KD.
Ku
1 + Ap + Bp2
2bl M éq + s f
2bS
, A=
2
2b (l f + S )
2b (l f + S 2 )
SciencesIndustriellespourl’Ingénieur
et 10/20
B=
s M éq
2b (l f + S2 )
. http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
b) Fonctiondetransfert
Elémentsdecorrection
Session2014
V ( p)
pour U( p) = 0 Fp ( p)
1
f + Méq p
2bl + s p
V ( p)
=
=
2b
1
Fp ( p)
(2bl + s p)( f + Méq p) + 2b S 2
⋅S2 ⋅
1+
U ( p )=0
f + Méq p
2bl + s p
æ
ö
2bl
ç2bl + s ÷÷ p
2 ç
2bl ÷ø
2b(l f + S ) èç
2bl + s p
=
=
sMéq
2blMéq + s f
2bl f + 2b S 2 + (2blMéq + s f )p + sMéq p2
2
p+
p
1+
2b(l f + S 2 )
2b(l f + S 2 )
K f (1 + t p)
=
1 + Ap + Bp2
Avec : K f =
2bl
s
ett =
. 2
2bl
2b(l f + S )
c) D’aprèsleschéma‐blocdelafigure12ona: V ( p) = H( p).G( p).U( p)- H( p).F ( p).Fp ( p) Donc: H( p).G( p) =
D’où : H( p) =
K f (1 + t p)
Ku
et H( p).F ( p) =
. 2
1 + Ap + Bp
1 + Ap + Bp2
1
, G( p) = K u et F ( p) = K f (1 + t p) .
1 + Ap + Bp2
Question15: a) Mettrelafonctiondetransfert
V ( p)
V ( p)
sousforme:
=
U( p)
U( p)
Ku
,
2x
p2
1+ p + 2
wn
wn
Donnerlesexpressionsdexet wn enfonctiondeAetB.
b) DonnerlavaleurdexpourquelaréponseenvitesseàunéchelondetensionU0soitla
plusrapidepossiblesansqu’ilyaitdépassement
c) Enfaisantusagedel’abaquedelafigure13,déterminerlavaleurde wn donnantun
tempsderéponseà5%égalà0,5s.
d) DéterminerlavaleurdugainKuassurantunevitesseenrégimepermanentde50m/s
pourunéchelondetensionU0=10Venl’absencedelaperturbation.
e) Enl’absencedelatensionU(p),déterminerlapositionenrégimepermanent x(¥) du
chariot1suiteàuneperturbationimpulsiondeDirac: Fp (t ) = a.d(t ) enfonctiondeKf.
f) Conclurequantlacapacitédelacommandeenchaînedirecteàsatisfairel’exigencedu
cahierdechargesentermesdesensibilitéàlaperturbation.
a)
Ku
V ( p)
=
=
U( p) 1 + Ap + Bp2
Ku
1
A
 wn =
et x =
2
p
2x
B
2 B
1+ p + 2
wn
wn
b) PourquelaréponseenvitesseàunéchelondetensionU0soitlaplusrapidepossiblesansqu’il
yaitdépassementilfautprendre x = 1 .
c) D’aprèsl’abaque,pour x = 1 ona: t r 5% .wn = 5  wn = 5/ t r 5% = 5/ 0,5 = 10 rad .s-1 .
SciencesIndustriellespourl’Ingénieur
11/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
d) Enl’absencedelaperturbation,lavitesseenrégimepermanent
v(¥) = K .U0  K = v(¥)/ U0 = 50 /10 = 5 m.s -1 .V -1 .
Donc:
V ( p)
5
=
U( p) (1 + 0,1.p)2
e) Enl’absencedelatensionU(p),Lapositionenrégimepermanentest:
K f (1 + t p)
1
x(¥) = lim pX ( p) = lim p.F ( p).H( p). Fp ( p) = lim
.1 = K f p 0
p 0
p0 1 + Ap + Bp2
p
f) Lacommandeenchaînedirecteestdoncsensibleuneperturbationimpulsion.Ellenejamais
satisfairel’exigenceducahierdechargesentermesdesensibilitéàlaperturbationimpulsion.
7.3.Synthèsedelaloidecommandedédiéeàl’asservissementetàlarégulationdelaposition
duchariot1
7.3.1.Systèmeasservinoncorrigé
Lapremièreétudeproposées’intéresseàl’étudedelacommandeenboucleferméenoncorrigé:C(p)=1.
Question16: a) Déterminerlafonctiondetransfertenboucleouverte H BO ( p) ensupposant Fp ( p) = 0 .
b) Déterminerlafonctiondetransfertenbouclefermée: H BF ( p) = X ( p)/ X C ( p) .
c) En supposant X C ( p) = 0 , déterminer la fonction de sensibilité vis‐à‐vis de la
perturbationdéfiniepar: H préc ( p) = e( p)/ Fp ( p) .
1
5
a) Fonctiondetransfertenboucleouverte: H BO ( p) = C( p).G( p).H( p). =
p p(1 + 0,1p)2
b) Fonctiondetransfertenbouclefermée:
H BO ( p)
X ( p)
5
1
H BF ( p) =
=
=
=
2
X C ( p) 1 + H BO ( p) 5 + p(1 + 0,1p)
1 + 0,2p + 0,02p2
c) Fonctiondesensibilitévis‐à‐visdelaperturbation:
2(1 + 0,2p)
1
F ( p).H( p).
2(1 + 0,2p)
e( p)
p
p(1 + 0,1p)2
H préc ( p) =
=
=
=
2
5
Fp ( p)
1 + H BO ( p)
5
+
p
(1
+
0,1
p
)
1+
p(1 + 0,1p)2
Question17: a) Donnerl’écartenrégimepermanentdûàuneentréeéchelon: x c (t ) = 0,01.u(t ) avec
u(t ) lafonctiond’Heaviside.
b) Déterminerl’écartenrégimepermanentdûàuneperturbationdetypeimpulsionde
Dirac: Fp (t ) = a.d(t ) .
c) Conclure quant à la capacité de la commande bouclée non corrigée à respecter les
spécificationsducahierdechargesentermesdeprécision.
a) Ecartenrégimepermanentdûàuneentréeéchelon:es=0carlaclassedeHBO(p)estégaleà1.
b) EcartenrégimepermanentdûàuneperturbationdetypeimpulsiondeDirac: Fp (t ) = a.d(t ) .
SciencesIndustriellespourl’Ingénieur
12/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
e(¥) = lim pe( p) = lim p.H préc ( p).Fp ( p) = lim p.
p 0
p 0
p 0
Session2014
2(1 + 0,2p)
.1 = 0 5 + p(1 + 0,1p)2
Résultatqu’onpourraitécriredirectementvuqu’unecommandeasservieesttoujoursinsensible
auxperturbationsimpulsionsetceciqu’ilyaitprésenced’intégrationdanslaboucleoupas.
c) Onconclutquelacommandeboucléenoncorrigéeestcapablederespecterlesspécificationsdu
cahierdechargesentermesdeprécision.
Question18: a) SurlafigureR5dudocument‐réponseDR4,placeretrelever:
 lapulsation wc 0 decoupureà0dB.

lesmargesdegainetdephase.
b) Lacommandeboucléenoncorrigéepermet‐ellederespecterlescritèresducahierde
chargesrelatifsàlarapidité,àlastabilitéetl’amortissementdel’axe?
a) Voirdocument‐réponseDR4
 lapulsation wc 0 =4rad/s.
 lesmargesdegainetdephase:MG=12dBetMP=45°.
b) Lacommandeboucléenoncorrigéepermetderespecterlecritèreducahierdechargesrelatifà
lastabilité(MP³45°)maispasceuxdelarapidité( wc 0 <10rad/s)etdel’amortissementde
l’axe(présencededépassementdelavaleurfinale)
7.3.2.Correctionàactionproportionnelle
Question19: a) ApartirdelafigureR5dudocument‐réponseDR4,déterminerlavaleurKc1deKc
permettantderespecterlaspécificationderapiditéexigéparleCdCF.
b) TracersurlafigureR5dudocument‐réponseDR4lesdiagrammesdegainetde
phasedusystèmecorrigéparKc1.
c) Releverlesnouvellesvaleursdesmargesdegainetdephase.
d) Auvudesrésultatsprécédents,est‐ilpossibledevaliderlechoixd’uncorrecteuràaction
proportionnel?Commenter.
a) ValeurKc1deKcpermettantderespecterlaspécificationderapiditéexigéeparleCdCF.
Ilfaudradéplacerlelieudegainverslehautpourlefairecouperavecl’axe0dBenw=10rad/s.
Lavaleurdedéplacementest20logKc1=12dBc.à.d.Kc1=1012/20=4.
b) Voirledocument‐réponse(lelieudephaseresteinchangé).
c) Nouvellesvaleursdesmargesdegainetdephase:MG=0dBetMP=0°lesystèmeestdevenu
justeinstable.
d) Il n’est pas possible de valider le choix d’un correcteur à action proportionnel car on ne peut
satisfaireàlafoisauxexigencesderapiditéetdestabilité:
PourKc=1,lecritèredestabilitéestsatisfaitmaispasceluidelarapidité;
PourKc=Kc1,lecritèrederapiditéestsatisfaitmaispasceluidelastabilité.
SciencesIndustriellespourl’Ingénieur
13/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
Question20:Apartirdelafigure15,justifierpourquoiest‐ilpossibled’approcherlesystèmeasservipar
un système de deuxième ordre et déterminer ses paramètres caractéristiques:
K BF , wnBF et xBF .
Ilestpossibled’approcherlesystèmeasserviparunsystèmededeuxièmeordredontlecoefficient
d’amortissementestinférieurà1,carlatangenteàl’origineesthorizontaleestquelaréponseest
oscillante.
Paramètrescaractéristiques:
Lapositionenrégimepermanentest: x(¥) = 0,01.K BF etonrelèvesurlegraphe x(¥) = 0,01m ,
donc: K BF = 1 .
æ -px ö÷
ln(D1 )
Le1erdépassementrelatifest D1 = expçç
,onrelèvesurlegraphe
÷÷  x =
2
2
ççè 1 - x ø÷
p + ln2 (D1 )
D1 =
0,0125 - 0,01
= 0,25 ,donc: x = 0,4 .
0,01
Le1erdépassementalieuàlademipseudo‐période.

Tp
2
=
p
wn 1 - x
2
= 0,65s  wn =
p
0,65 1 - x
2
,donc: wn  5,3rad.s-1 .
7.3.3Correctionàactionsproportionnelle‐dérivée
Question21:SurlafigureR6dudocument‐réponseDR4,tracerlesdiagrammesasymptotiqueset
l’alluredesdiagrammesréelsdeBodeducorrecteur C2 ( p) .
VoirDocument‐réponseDR4.
Question22:Déterminerlafonctiondetransfertenboucleouvertecorrigé H BO 2 ( p) ,donnersonordre,sa
classeetsongainstatique.
H BO 2 ( p) = 1,65⋅
1 + 0,24.p
5
8,25(1 + 0,24p)
⋅
=
2
1 + 0,04.p p(1 + 0,1p)
p(1 + 0,04.p)(1 + 0,1p)2
Sonordren=4,saclassea=1etsongainstatiqueKBO2=8,25.
Question23: a) Représenter puis relever les écarts en régime permanent respectivement à une
perturbationimpulsion Fp (t ) = a.d(t ) etàunéchelondeposition x c (t ) = 0,01.u(t ) .
b) Représenter puis relever sur le diagramme de Black de la figureR8 du document‐
réponseDR5,lapulsation wc 0 decoupureà0dB,lesmargesdephaseetdegain.
c) Au vu des résultats précédents et des spécifications du cahier des charges, est‐il
possibledevaliderlecorrecteuràactionproportionnelle‐dérivée C2 ( p) ?Commenter.
a)
‐L’écartenrégimepermanentàuneperturbationimpulsion Fp (t ) = a.d(t ) est nulcarlesystème
estbouclé.
SciencesIndustriellespourl’Ingénieur
14/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
Elémentsdecorrection
Session2014
‐ L’écart en régime permanent à un échelon de position x c (t ) = 0,01.u(t ) est aussi nul car la
boucleprésenteuneintégration.Voirdocument‐réponseDR5
b) ‐Pulsationdecoupureà0dB: wc 0 = 10 rad .s-1 .
‐Margesdephaseetdegain: MP  45 etMG  12dB.
c) Cecorrecteurpermetlasatisfactiondescritèresducahierdechargesentermesdeprécision,
rapiditéetdestabilitémaispasceluidel’amortissementdel’axe(onvoitbiensurlegraphede
positionlaprésenced’ndépassementtransitoire.Onnepeutpasalorslevalider.
Question24: a) ReleversurlediagrammedeBodedelafigure21,lapulsation wc 0 decoupureà0dB
ainsiquelesmargesdegainetdephase.
b) Cettecommandepermet‐ellederespecterlescritèresdeperformancesdéfinisparle
cahierdescharges?Commenter.
a) ‐Pulsationdecoupureà0dB: wc 0 = 10 rad .s-1 .
‐Margesdephaseetdegain: MP = 77 etMG=40dB.
b) Cettecommandepermetderespectertouslescritèresdeperformancesdéfinisparlecahierdes
charges,eneffet:
–Pourlaprécision:lesécartsdusàlaperturbationimpulsionetàl’entréeéchelonsonttoutdeux
nuls.
–Pourlarapidité: wc 0 = 10 rad .s-1 ;
–Pourlastabilité:MP>45°;
–Pourl’amortissementdel’axe:onvoitbiensurlegraphed’évolutiondelapositionqu’iln’yapas
dépassementtransitoire.
…Fin
SciencesIndustriellespourl’Ingénieur
15/20
http://al9ahira.com
TournezlapageS.V.P.
ConcoursNationalCommun
FT1:Traiteautomatiquement
unevacheetluifournirune
quantitédenourritureadaptée.
FigureR1:FASTpartiel
durobotdeTraite
AstronautA3
Elémentsdecorrection
Session2014
DOCUMENT‐REPONSEDR1
Unitédecommande
etmodèlede
décision
FT10:Gérerla
traite
FT11:Recevoir
lavache
FT111:………………
…………………………
Placerlavache
………………………….
FT112:Isolerla
vache
FT12:
Transmettreau
robotles
caractéristiques
delavache.
FT13:
Extrairelelait
FT14:Analyser
etstockerlelait
FT15:……………
Dialogueravec
…………………….
l’utilisateur
SciencesIndustriellespourl’Ingénieur
16/20
Box
Portesentrée
…………………………
etsortie
………………………….
FT121:Identifier
lavache
…………………………
Lecteurdu
……………………..
badgedela
FT122:Peserla
vache
Plateaupeseur
………………………..
FT123:Traiterles
informationset
transmettreles
données
Ordinateurde
……………………….
stockagede
…………………………
l’information
…………………………
FT131:Mettreen
positionlesdivers
organesnécessaires
à la traite
Brasdurobot,
chariot,vérins
FT132:………………
Détecterles
…………………………
positions
……………………….
destrayons
Systèmede
détectiondes
trayons
FT133:Nettoyer
lestrayons
Brosses
……………………....
FT134:Connecter
lavacheaurobot
Système
d’aspirationet
gobelets
FT135:Réguleret
asservirla
positiondesdivers
organesdetraite
Lesboucles
d’asservissements
FT141:Recevoir
le lait
Cuvederéception
dulait
FT142:Déterminer
laconductivité,la
couleur,ledébitdu
lait
…………………………
CapteurMQC
…………………………
FT143:Peserlelait
Balance
……………………….
Ecrandecontrôle
tactile
http://al9ahira.com
Document‐‐réponse
ConcoursNationalCommun
Elémentsdecorrection
Session2014
DOCUMENT‐R
EPONSEDR2
10 poids >250 11 Fermer porte entrée Acquérir données du badge traite non autorisée porte entrée fermée.données reçues.traite autorisée 30 Nettoyer trayons 12
Ouvrir porte sortie brossage terminé détection vache sortie 40 Localiser trayons 13
Fermer porte sortie trayons localisés Ouvrir porte entrée M50 « Accrocher gobelets » porte entrée ouverte.porte sortie fermée gobelets rétractés
60 Escamoter gobelets gobelets escamotés 70 Rincer trayons cycle rinçage trayons terminé 71 74
Ouvrir porte sortie Rincer canalisations, gobelets et b
cycle rinçage gobelets terminé détection vache sortie 72 75
Fermer porte sortie Transmettre données Placer bras en position attente Ouvrir porte entrée données transmises . bras en position porte entrée ouverte . porte sortie 73 76
1
FigureR2:GrafcetG1degestiondestâchesàcompléter
SciencesIndustriellespourl’Ingénieur
17/20
http://al9ahira.com
Document‐‐réponse
ConcoursNationalCommun
Elémentsdecorrection
Session2014
EPONSEDR3
DOCUMENT‐R
0
O
1º0
Echelledesvitesses:0,1m/s1,5cm

V ( B Î 2/ 0)
I30

V ( D Î 2/ 0)

V (D Î 50/0)

z0 
V ( D Î 51 / 50)

dir. V ( E Î 3/ 0)
J
2
B
3
D
E
51
A

V (G4 Î 4 / 0)
6
C
4
50
G4
F
FigureR3 :Schémacinématique
plandubrasderobot

y0 H

NM
h
Galet2
Bâti0

RM
Galet1

N TN
j
Galet3

NN

TM
M
j

RN
Galet4
Chariot1
e/2
e/2

z0
L
Llim

x0 FigureR4:Schémaduguidage
duchariot1

F1
K
SciencesIndustriellespourl’Ingénieur
I
18/20
http://al9ahira.com
Document‐‐réponse
ConcoursNationalCommun
Elémentsdecorrection
Session2014
DOCUMENT‐R EPONSEDR4
Phase(deg)
Gain(dB)
40
20
0
‐20
‐40
‐60
‐80
‐100
‐120
‐90
‐135
‐180
‐225
‐270 ‐
10
wc0
wc0’
MG=12dB
Lieudugaindusystème
corrigéavecKc=Kc1
20logKc1=12dB
Mêmelieudelaphasepourle
systèmecorrigéavecKc=Kc1et
noncorrigé
MP=45°
0
10
1
10
2
Pulsation(rad/s) 10
3
10
FigureR5:DiagrammedeBodedelaboucleouvertedusystèmeasservinoncorrigé
Gain(dB)
20
16
12
8
4
20log1,65
0
90
45
1
0,04
Phase(deg)
1
0,24
0
1
2
3
10
10 Pulsation(rad/s) 10
FigureR6:DiagrammedeBodeducorrecteuràactionsproportionnelleetdérivéeC2(p)
‐1
10
0
10
SciencesIndustriellespourl’Ingénieur
19/20
http://al9ahira.com
Document‐‐réponse
ConcoursNationalCommun
Elémentsdecorrection
Session2014
DOCUMENT‐REPONSEDR5
Positionx(t)(m)
0,014
0,012
s = 0
0,010
0,008
0,006
0,004
0,002
0
0
0,5
1
1,5
2
2,5
3
3,5
Temps(s)
FigureR7:Positionduchariot1pourunéchelondepositionde0,01maveclecorrecteurC2(p)
60
0,1rad/s
40
1rad/s
MP  45°
0
MG  12dB
6rad/s
=10
rad/s
0
Gain(dB)
20
ωc
‐20
30rad/s
‐40
16rad/s
70rad/s
‐60
‐80
300rad/s
‐100
‐120
‐270
‐225
‐180
Phase(deg)
‐135
‐90
FigureR8:DiagrammedeBlackdelaboucleouvertecorrigéeaveclecorrecteurC2(p)
SciencesIndustriellespourl’Ingénieur
20/20
http://al9ahira.com
Document‐‐réponse
Rien ne saurait remplacer un livre en papier
Des livres de prépas très joliment imprimés
à des prix très accessibles
Al9ahira
En 3 clics seulement, on livre, tu étudies
en ligne
La qualité est notre point fort.
Vos commentaires sont importants pour nous
Pour toute information, n’hésitez pas à nous contacter
mailto:al9ahira@gmail.com
http://al9ahira.com/
Tél : 0539/34 33 20
7, rue Égypte. Tanger