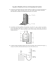Ejercicios extraídos desde Guías de Coordinación Certamen 1

Ejercicios
(extra´ıdos desde Gu´ıas de Coordinaci´
on)
MAT 021/ C´alculo
1. Calcular los valores de k para que una ra´ız de la ecuaci´on:
(k 2 − 3)x2 − 3(k − 1)x − 5k = 0
sea −2.
2. Una furgoneta pesa 875 kg. La diferencia entre el peso de la furgoneta vac´ıa y el peso de la carga
que lleve no debe ser inferior que 415 kg. Si hay que cargar cuatro cajones iguales, ¿cu´anto puede
pesar, como m´
aximo, cada uno de ellos para poder llevarlos en esa furgoneta?
3. El n´
umero de diagonales de un pol´ıgono de n lados est´a dado por D =
pol´ıgono que tiene a lo m´
as 54 diagonales.
n(n−3)
.
2
Encontrar el
4. Un rect´
angulo de 12 mt de largo y 10 mt de ancho se les cortan cuadraditos en cada una de sus
esquinas (congruentes) de lado x. Determinar los posibles valores de x para que el ´area de la base
de la caja est´e entre 48 y 52 metros cuadrados.
5. Resuelva la ecuaci´
on:
q
q
√
√
x + 3 − 4 x − 1 − x + 8 − 6 x − 1 = 1.
6. Sean
x∈R:
A=
x3 + x
≥ x2 + 1
x+3
y
B = {x ∈ R : |x + 5| < 1}.
c
Determine el conjunto A ∩ B .
7. Considere la ecuaci´
on
1
= 0.
4
Determine los valores de α de modo que la ecuaci´on no tenga ra´ıces reales y adem´as se verifique
que
α ∈ {x ∈ R : |3x + 1| < |2x − 1|} .
(α + 1)x2 + (α − 1)x +
8. Sabiendo que f (x) = 3x + 2, determine la funci´on real g tal que:
(f ◦ g ◦ f )(x) = 6x + 7.
9. Sea f : R → R tal que
3x2 − 1
3x − 1
si x > 2
si x ≤ 2
3x − 2
x−1
si x > 0
si x ≤ 0
f (x) =
y sea g : R → R tal que
g(x) =
a) Determine f ◦ g.
b) Determine g ◦ f .
10. Sea g : R → R tal que
g(x) =
3x
√ +6
1−x−1
y sea f : D ⊂ R → R tal que
si x ≥ 1
si x < 1
1
.
1−x
a) Restringa adecuadamente el dominio y el condominio de f y g de modo que ambas sean
funciones biyectivas.
b) Determine g ◦ f .
f (x) = √
1
2
11. Pruebe que cualquier funci´
on se puede expresar como la suma de una funci´on par y una funci´
on
impar. Indicaci´
on: Note que f (x) = 12 (f (x) + f (−x)) + 21 (f (x) − f (−x)).
12. Sea f (x) =
√1
.
1+ 3x+2
√
Determine Dom(f ), Rec(f ), y verifique si existe x ∈ R tal que f (x) =
3−1
2 .
13. En una esfera se inscribe un cono (regular recto). Determine la funci´on volumen del cono en
t´erminos del ´
angulo del v´ertice.
14. En un tri´
angulo equil´
atero de lado a se inscribe un rect´angulo, de modo que una de las aristas
del rect´
angulo est´
a en la base del tri´angulo. Al hacer rotar este rect´angulo en torno a la base del
tri´
angulo, se obtiene un cilindro. Determine una expresi´on para el volumen de este cilindro, en
funci´
on del radio del mismo.
15. Una pared de 10 pies se halla a 5 pies de distancia de un edificio.Una escalera, apoyada en la
pared, toca el edificio como se muestra en la figura abajo. Exprese la longitud de la escalera como
una funci´
on de x.