Tentamen i Beräkningsvetenskap I/KF, 5.0 hp, 2015-03

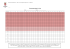
Uppsala universitet
Institutionen för informationsteknologi
Teknisk databehandling
Tentamen i Beräkningsvetenskap I/KF, 5.0 hp, 2015-03-17
Skrivtid: 1400 − 1700 (OBS! Tre timmars skrivtid!)
Hjälpmedel: Bifogat formelblad och miniräknare.
För fullt uppfyllda mål och kriterier på uppgifterna krävs fullständiga räkningar och utförliga
resonemang samt motivering till alla svar.
Kursmål (förkortade), hur de täcks i uppgifterna och maximalt betyg (med
reservation för modifieringar).
Fråga nr
1
2
3
4
5
6
7
Nyckelbegrepp Algoritmer Analys Programmering
3
(a) 3
(b) 3
3
(a) 3, (b) 3
(a) 3, (b) 3
4
4, 5
Del A
1. Matrisen A i ett linjärt ekvationssystem Ax = b har LU-faktoriserats till matriserna
L, U och P så att P A = LU . Matriserna är






1 0 0
1 2
1
0 1 0
1 
L =  0 1 0
U = 0 2
P = 0 0 1 .
1/2 0 1
0 0 −1/2
1 0 0
 
2

4 .
Använd LU-faktoriseringen för att lösa ekvationssystemet med b =
6
Utnyttja att L är undertriangulär och att U är övertriangulär för att spara beräkningar. Redovisa beräkningarna.
1
2. I figuren nedan visas den icke-linjära ekvationen sin(5x) + cos(3x) + 1 = 0 (x-värden
i radianer, inte grader).
3
2.5
2
f(x)
1.5
1
0.5
0
-0.5
-1
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
x
(a) Genom zoomning i plotten kan man se att första positiva roten ligger i intervallet
[0.6 0.8]. Visa att du behärskar Bisektionsmetoden genom att hitta denna rot
med den metoden. Använd intervallet ovan som startintervall, och iterera tills
lösningen har en decimals noggrannhet, dvs felet är < 0.05.
(b) Antag att du istället ska lösa samma problem (dvs hitta första positiva roten) på
en dator med Newton-Raphsons metod. Tyvärr har du inte plottat funktionen
och vet därför inte riktigt hur funktionen ser ut. Ange två problem som kan
uppstå.
3. En vän till dig har utvecklat en numerisk metod för att beräkna integraler. Din vän
påstår att metoden har noggrannhetsordning 3. För att undersöka om det verkligen
stämmer testar du metoden på en integral
Z 1
I=
f (x) dx ,
0
där f är en känd funktion, som är så pass enkel att du kan beräkna integralen analytiskt. När du diskretiserar integrationsintervallet med steglängden h = 0.2 finner
du att det absoluta felet |Iber − I| är 0.152, där Iber är det integralvärde som du beräknat med din väns metod. Förutsatt att metodens noggrannhetsordning verkligen
är 3, hur stort bör felet |Iber − I| bli, om du gör en ny beräkning med den mindre
steglängden h = 0.1?
2
4. (a) En iterativ metod för att lösa en icke-linjär ekvation med lösning x∗ = 0 ger
dessa rotuppskattningar i tre på varandra följande iterationer:
x1 = 0.1,
x2 = 0.01,
x3 = 0.0001.
Vilka av påståendena nedan stämmer? Kort motivering krävs
i.
ii.
iii.
iv.
Metoden
Metoden
Metoden
Metoden
har noggrannhetsordning 2.
har konvergenshastighet 2.
divergerar.
konvergerar.
(b) En av lärarna på kursen har i Matlab implementerat Simpsons metod för att
beräkna en integral numeriskt. Här används en ekvidistant indelning av integrationsintervallet, dvs steglängden h är densamma över hela intervallet. Då integralen beräknas med olika h finner man att det relativa felet i beräkningarna
ändras enligt grafen nedan. Uppenbarligen beter sig det relativa felet väldigt
annorlunda för h < 10−3 , jämfört med för h > 10−3 . Detta beror på att två
olika typer av fel påverkar beräkningarna. Ange vilken typ av fel är det som
dominerar för (i) h > 10−3 ? (ii) h < 10−3 ?
10 -2
10 -4
relativt fel
10 -6
10 -8
10 -10
10 -12
10 -14
10 -16
10 -10
10 -8
10 -6
10 -4
h
3
10 -2
10 0
5. (a) Vad skrivs ut på skärmen när följande program körs?
N = 3;
j = 1;
for i = 1:N
if j > 2
disp(’i är: ’)
disp(i)
elseif j == 2
disp(’j är: ’)
disp(j)
else
disp(’i+j är: ’)
disp(i+j)
end
j = 2*j;
end
(b) I ett Matlab-program för att beräkna medelvärdet av en vektor x har raderna
tyvärr blivit slumpmässigt omkastade. Dessutom har en extra onödig rad tillkommit och indenteringen försvunnit. Återställ den sekvens av kodrader som
bildar programmet som beräknar medelvärdet av vektorn x och detta värde tilldelas variabeln medel vid programmets slut. Ange de sex kodradernas nummer
(t ex 2, 3, 4, 5, 6, 7) i den ordning som kodraderna måste skrivas för att bilda
programmet. Observera att en av raderna ska tas bort. Motivering behövs inte.
Nummer
1
2
3
4
5
6
7
Kodrad
end
for i=1:length(x)
x = [5 1 2 3 1];
medel = summa/length(x);
summa = summa + x(i);
summa = summa + i;
summa = 0;
4
Del B
Rb
6. När man löser integraler a f (x)dx numerisk kan integranden f (x) vara given antingen som en kontinuerlig funktion eller som en datamängd (en tabell) med t ex
mätvärden enligt
x2
···
f (x2 ) · · ·
xi
x1
f (xi ) f (x1 )
xn
f (xn )
Vi förutsätter här att antalet värden n i tabellen ska kunna vara vilket som helst,
dvs både udda eller jämnt antal.
(a) Under de här förutsättningarna, beskriv vilka metoder (av de som ingått i kursen, dvs Simpson eller Trapets) som är lämpliga i fallet då f (x) är en kontinuerlig
funktion, respektive när den given som diskret datamängd enligt ovan. Du måste
motivera ditt val av metod för de två fallen.
(b) Beskriv även det totala felet i de båda fallen, genom att ge formler för felen
där du med korrekt begreppsapparat kort beskriver de olika komponenterna i
formlerna.
(c) Du kan anta att f (xi ) (i tabellen ovan) har en noggrannhet på 3 korrekta decimaler, dvs att absoluta felet i f (xi )-värdena är ≤ 0.5 · 10−3 . På vilket sätt
påverkar detta felet? Vad i ditt uttryck i (b) påverkas.
7. Tryckförhållandena i knutpunkterna i vattenledningsnätet i Lutorp kan beräknas som
lösningen till det linjära ekvationssystemet
Ap = b,
där A är en n × n-matris, p och b är kolonnvektorer med vardera n element. Det
finns n stycken knutpunkter i vattenledningsnätet och vektorelementet pk är trycket
i knutpunkt nummer k.
Vattnet i nätet kommer från en vattenreservoar och vattentrycket i reservoaren avgör hur stort trycket blir i de olika knutpunkterna. Vi antar här att trycket i varje
knutpunkt är > 0. Vattentrycket r i reservoaren påverkar högerledet b, men inte
koefficientmatrisen A i ekvationssystemet ovan.
För att vattenledningssystemet ska fungera tillfredställande måste trycket i knutpunkterna överstiga ett undre värde c. Nu vill ingenjörer på Tekniska kontoret i
Lutorp beräkna hur stort trycket i vattenreservoaren minst behöver vara för att vattentrycket i knutpunkterna ska bli större än eller lika med c (den knutpunkt med det
lägsta trycket måste alltså minst vara c).
Din uppgift är beskriva hur man skulle kunna lösa detta problem och utforma ett
program eller algoritm för att bestämma det tryck i vattenreservoaren r som gör
5
att det minsta elementet i vektorn p får värdet c. Uttryck programmet i Matlab
eller Matlab-liknande notation. Du får använda Matlabs inbyggda kommandon för
att lösa olika typer av beräkningsproblem, så du behöver inte implementera en egen
numerisk metod. Vidare kan kommandot min(p) användas för att hitta minsta värdet
i vektorn p. Du får också anta att det finns en färdig Matlab-funktion hogerled(r),
som genererar ekvationssystemets högerled (dvs givet ett visst värde på r så skapas
högerledet).
Det blir inget avdrag för rena Matlab-fel, så länge det framgår att programmet i
princip är riktigt.
6