Imágenes en Matlab

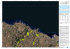
Imágenes en Matlab
Cristian S. Rocha, Andrea Manna, . . .
Taller 1
1.
Prefacio
Antes de empezar a trabajar con el Octavehay que asegurarse que la versión
en la que se trabaja no tiene ningún bug perdido.
Sabemos que en la versión 3.2.4 del octave no se puede mostrar imágenes.
La razón se puede leer en el wiki:
http://wiki.octave.org/wiki.pl?OctaveForWindows
y se resuelve ejecutando el siguiente comando de la linea de comandos:
pkg rebuild -noauto oct2mat
que deshabilita el módulo oct2mat cada vez que se inicia el Octave. Aparentemente este módulo es el que provoca el problema. Una vez deshabilitado se
reinicia el Octavey el comando imshow vuelve a funcionar.
2.
2.1.
Primera Parte
Introducción
Para trabajar computacionalmente con una imagen hay que interpretarla
como una función matemática. Algunas caracterı́sticas de una imagen guardada de una computadora es que tiene una cantidad finitas de puntos, es una
interpretación de una imagen original que deberı́a formarse por una cantidad
infinita (o mucha mas grande) de puntos. Cada punto de la imagen está indexado a través de valores naturales x, y que referencian a las coordenadas x e y
del plano. A su vez cada punto puede contener más de un canal asociado a una
frecuencia o energı́a que son capaces de reflejar”.
Imágenes
Definition 1 (Imágen). Una Imagen normalizada es una función
I : N2+1 → [0, 1]
Cada tupla de naturales x, y : N2 se la conoce como pixel. Y cada valor I(x, y, c)
es la intensidad asociada al pixel (x, y) del canal c.
1
Existen varias formas de representar la luz reflejada por los puntos, pero la
más común es descomponiendola en colores primarios rojo, verde y azul. La
descomposición se asocia a canales (c) cuyos valores se encuentran en general
entre 0 y 1, indicando el 0 la falta total de ese canal y 1 la intensidad máxima
de ese canal. Por ejemplo en la representación RGB tener todos los canales en 1
representan el color blanco, y tener todos los canales en 0 representan el negro.
Esto puede variar según la descomposición elegida.
Los canales más conocidos son Rojo, Verde y Azul (RGB), aunque existen
otras combinaciones (ACM), (CMYK), (HSV), (YUV), . . .
Una imagen con un único canal se lo conoce como imagen de escala de grises.
La idea de Imagenes normalizadas surge porque existen muchas formas de
almacenar esas imágenes en la computadora. Es común encontrar que los valores
sean entre 0 y 255 ya que se almacenan en la computadora con 8 bits o un byte.
Y en general 256 valores son suficientes. Otro es el caso que la imagen provenga
de satélites, o se quiera representar imágenes con mayor cantidad de colores.
Pero ese es un tema del cual no vamos a hablar.
Canales
Imagen RGB sin descomponer
Canal Rojo
2.2.
Canal Verde
Canal Azul
Procesamiento básico de imágenes
La forma más tradicional para trabajar con Imágenes es interpretando que
son matrices de 2 + 1 dimensiones.
En Octavelas operaciones de lectura y escritura de imágenes son imread y
imwrite. Para imread el nombre del archivo es suficiente para devolver una matriz de la cantidad de pixels y canales que almacena el archivo. Para almacenar
una matriz como una imagen hay que indicar en que formato se debe almacenar. Para ver la imagen se usa el comando imshow cuyo parámetro de entrada
es la matriz a mostrar como una imagen. Utilicen estos comandos y averigüen
2
la resolución (Cantidad de pixels en los ejes X e Y) que tiene la imagen usando
el comando size
Empezando a trabajar con imágenes en Octave y Matlab
> A = imread(’lena std.tif’);
> imwrite(A, ’lena std.tif’, ’tif’);
> imshow(A);
Proponer que generen las imágenes en escala de grises a partir de los canales
Rojos, Verdes y Azul de la imagen. Se pueden obtener pidiendo la submatriz
A(:, :, 1), A(:, :, 2), A(:, :, 3) respectivamente. Aquı́ puede verse como la imagen
tiene una resolución de 512x512 pixels y tres canales correspondientes a los
canales del RGB. Mostramos el canal rojo en escalas de grises con el comando
imshow. El comando imshow siempre toman al canal rojo, verde y azul como
esas submatrices. También puede usarse la función imfinfo para conocer la información de la imagen.
Empezando a trabajar con imágenes en Octave y Matlab
> A = imread(’lena std.tif’);
> size(A)
ans =
512
512
3
> imshow(A(:,:,1))
> imfinfo(’lena std.tif’)
...
Para confirmar que la imagen no está normalizada obtener el máximo y
mı́nimo valor de la matriz usando las funciones max y min. Notar que hay que
repetir las funciones porque se aplican sucesivamente en cada dimensión de la
matriz. En este caso las imágenes no están normalizadas.
Empezando a trabajar con imágenes en Octave y Matlab
> A = imread(’lena std.tif’);
> max(max(max(A)))
ans = 255
3
> min(min(min(A)))
ans = 3
Para normalizar la imagen se puede realizar la siguiente operación. La función double convierte la matriz de números enteros a números reales y 255
normaliza los valores.
Empezando a trabajar con imágenes en Octave y Matlab
> A = imread(’lena std.tif’);
> N = double(A) / 255;
> imshow(N)
2.3.
Ejercicios
A partir de aquı́ se proponen los siguientes ejercicios.
Ejercicio
Represente la imagen de Lena apagando los diferentes canales. Esto pude
hacerse asignando 0 a cada canal.
Deje encendido solo el canal Rojo.
Deje encendido solo el canal Verde.
Deje encendido solo el canal Azul.
Deje encendido solo los canales Rojo y Verde.
Deje encendido solo los canales Verde y Azul.
Deje encendido solo los canales Rojo y Azul.
Para ello recomiendo copiar la imagen a una matriz temporal e ir apagando
los canales de a poco. A continuación solo apagamos el canal Rojo.
Solución
> A = imread(’lena std.tif’);
> T = A
> T(:,:,2) = 0
4
> T(:,:,3) = 0
> imshow(T)
El siguiente ejercicio ayuda a reconstruir una imagen a partir de canales
calculados en forma independiente. Se introduce la función ndgrid que permite
generar matrices a partir del ı́ndice.
Ejercicio
Se pide reconstruir una imagen a partir de canales generados a partir de las
siguientes funciones.
r(x, y) = sin(x) + sin(y)
g(x, y) = sin(x + ,25π) + sin(y + ,25π)
b(x, y) = sin(x + ,5π) + sin(y + ,5π)
Solución
> X = ndgrid(0:0.1:2*pi,0:0.1:2*pi);
> Y = X’;
> R = 0.5+sin(X)+sin(Y);
> G = 0.5+sin(X+0.25*pi)+sin(Y+0.25*pi);
> B = 0.5+sin(X+0.5*pi)+sin(Y+0.5*pi);
> I = zeros(size(R,1), size(R,2), 3);
> I(:,:,1)=R;
> I(:,:,2)=G;
> I(:,:,2)=B;
> imshow(I)
El siguiente ejercicio introduce el uso de la función hist para conocer la
distribución de la intensidad de los diferentes canales. Esto nos permite realizar
otras operaciones a futuro.
5
Ejercicio
Represente el histograma por cada canal.
Rojo.
Verde.
Azul.
Supongo que saben realizar estas operaciones. Las vieron en una clase anterior.
Ahora la idea es jugar con partes de imágenes.
Ejercicio
Se pide intercambiar el cuarto superior izquierdo de la imagen con el cuarto
inferior derecho.
Resultado
> L = imread(’lena std.tif’);
> Qsi = L(1:256,1:256,:);
> Qid = L(257:512,257:512,:);
> L(257:512,257:512,:)=Qsi;
> L(1:256,1:256,:)=Qid;
> imshow(L)
6
3.
3.1.
Segunda Parte
Operaciones de matrices y resultados en imágenes
Antes de cualquier cosa debemos poder crear imágenes vacı́as para poder
almacenar resultados en ellas. Ahora hay que hablar de cómo crear matrices que
sean compatibles con las imágenes, porque sino no se va a poder almacenarlas
ni verlas.
Creación de imágenes vacias
Las imágenes se crean como cualquier matriz, pero hay que indicar que el
tipo de dato a usar es de tipo byte.
> zeros( [10,10,3], ’uint8’)
Algunas operaciones sobre matrices tienen efectos interesantes en las imágenes.
Ahora enumeraremos algunas de estas operaciones.
Operaciones
Siendo M la matriz de la imagen, I la matriz identidad y E es la matriz
identidad espejada.
Espejado diagonal D = M t .
Espejado horizontal H = M · E
Espejado vertical V = E · M
El problema principal de trabajar con estas operaciones es conseguir la matriz identidad del tamaño adecuada y asegurarse que la imagen es cuadrada. Recuerden que la multiplicación de matrices require equivalencia entre el tamaño
de las matrices. Se pueden multiplicar una imagen M de n × m por una matriz
I de m × p, y el resultado será una matriz de n × p. Es por eso que recomiendo
usar matrices cuadradas. Para eso es necesario generar una matriz más grande
donde almacenar la imagen si es que esta no es cuadrada.
A continuación muestro cómo encuadrar la imagen. Cargo primero una imagen que no es cuadrada y la copio a una imagen pre-creada cuadrada del tamaño
adecuado.
Encuadrar una Imagen
> S = imread(’san diego.tif’);
> c = size(S,3);
> n = max(size(S)(1:2));
> D = zeros([n,n,3],’uint8’);
7
> D(1:size(S,1),1:size(S,2),:) = S;
En el caso que no se quiera utilizar operaciones con matrices porque tardan
mucho tiempo en resolverse o porque una matriz no puede resolver el problema, se puede calcular con una doble iteración sobre el las filas y las columnas
respectivamente.
Aquı́ por ejemplo mostramos como calcular cual es el valor promedio que
hay en los pixels de la imagen en el canal 1.
Modificar una imagen
> I = imread(’san diego.tif’);
> s =0;
> for i in 1:size(I,1)
> for j in 1:size(I,2)
> s = s + double(I(i,j,1));
> end
> end
> s/(size(I,1)*size(I,2))
3.2.
Ejercicios
Ahora vamos a resolver algunos ejercicios de traslación y rotación.
Primero vamos a encuadrar la imagen y centrar.
Ejercicio
Encuadrar y centrar la imagen san diego.tif en una nueva matriz.
Solución
> I = imread(’san diego.tif’);
> n = max(size(I)(1:2));
> D = zeros([n, n, size(I,3)], ’uint8’);
> top = (n - size(I,1)) / 2 + 1;
8
> left = (n - size(I,2)) / 2 + 1;
> D(top:top+size(I,1)-1, left:left+size(I,2)-1, :) = I;
> imshow(D);
Ahora vamos a rotar las imágenes. Una función importante para rotar es
fliplr que realiza un espejo vertical. Aunque esta función puede resolver todo el
problema, lo interesante es usarla para conseguir la matriz identidad espejada
y luego aplicarla para rotar en horizontal y vertical.
Otro tema al que hay que prestar atención es que no se pueden multiplicar
matrices de tipo ’uint8’. Lo que si se puede hacer es convertirlas en matrices de
tipo ’double’, multiplicar y luego volver a ’uint8’.
Ejercicio
Se pide realizar un espejado vertical y horizontal de lena.
Solución
> I = imread(’lena std.tif’);
> E = eye(size(I)(1:2));
> E = fliplr(E);
> D = uint8(double(I(:,:,1))*double(E));
> showim(D);
> D = uint8(double(E)*double(I(:,:,1)));
> showim(D);
Ahora vamos a rotar la imagen 90 grados.
Ejercicio
Rotar 90 grados la imagen de lena.
Para la solución podemos realizar un espejado diagonal para luego realizar
una espejado horizontal. O al revés. . .
Solución
> I = imread(’lena std.tif’);
> E = eye(size(I)(1:2));
9
> E = fliplr(E);
> D = uint8(double(I(:,:,1))*double(E));
> D = uint8(double(D)’);
> showim(D);
Este es un ejercicio difı́cil de resolver, pero es un ejercicio bien completo.
Ejercicio
Se busca una función que permita re-escalar una imagen.
Ayuda: Usar las funciones meshgrid y linspace para “rehubicar los pixels”
La función meshgrid genera las coordenadas de una grilla de N dimensiones
asociada a una matriz.
Aquı́ se presenta un ejemplo de lo que meshgrid devuelve
Meshgrid
> [XX,YY] = meshgrid(0:0.2:1,0:0.2:1)
XX =
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.20000
0.40000
0.60000
0.80000
1.00000
0.00000
0.00000
0.00000
0.00000
0.00000
0.00000
0.20000
0.20000
0.20000
0.20000
0.20000
0.20000
0.40000
0.40000
0.40000
0.40000
0.40000
0.40000
0.60000
0.60000
0.60000
0.60000
0.60000
0.60000
0.80000
0.80000
0.80000
0.80000
0.80000
0.80000
YY =
10
1.00000
1.00000
1.00000
1.00000
1.00000
1.00000
Por ejemplo, tenemos una matriz M de 5x5 que representa valores en un
espacio bidimensional de 0 a 1. Entonces si queremos conocer en que posición
debe ir el valor de M (1, 2) , entonces podemos fijarnos en las matrices resultantes
de meshgrid, que en este caso está asociado a la coordenada XX(1), Y Y (1).
Meshgrid
> A = eyes(5);
> [XX,YY] = meshgrid(0:1/(size(A,1)-1):1,
0:1/(size(A,2)-1):1);
> XX[1], YY[2], A(1,2)
ans = 0
ans =
0.20000
ans = 0
En combinación con linspace se puede realizar varias tareas de interpolación
lineal.
la función linspace(a,b,n) permite generar n valores intermedios entre dos
valores a y b en forma lineal. Muy parecido a lo que realizamos previamente con
la generación de un vector por rango, excepto que linspace es más elegante.
Linspace
> linspace(0, 1, 5)
ans =
0.00000
0.25000
0.50000
0.75000
1.00000
> 0:1/(5-1):1
ans =
0.00000
0.25000
0.50000
0.75000
1.00000
Ahora esta interpolación puede usarse para conocer que pixel debe asociarse
a la matriz resultante. La función meshgrid me permite conocer como se reordenan los nuevos pixels. La función round pasa los valores reales a valores enteros
11
que representan donde están los pixels originales correspondiente a ese punto de
la matriz.
Entonces la solución a este problema es el siguiente:
Solución
function [ ret ] = imagezoom (I, factor)
[ width, height, c ] = size(I);
new width = width * factor;
new height = height * factor;
ret = zeros([new width, new height, c], ’uint8’);
[XX, YY] = meshgrid(linspace(1,width,new width),
linspace(1,height,new height));
XX = round(XX);
YY = round(YY);
for i = 1:new width
for j = 1:new height
ret(i,j,:) = I(XX(j,i),YY(j,i),:);
end
end
endfunction
12