Übungen mit dem Applet „Wahrscheinlichkeitsnetz“

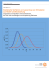
Wahrscheinlichkeitsnetz
1
Übungen mit dem Applet
„Wahrscheinlichkeitsnetz“
1
2
3
Statistischer Hintergrund........................................................................... 2
1.1
Verteilungen ..........................................................................................................2
1.2
Darstellung von Daten im Wahrscheinlichkeitsnetz ...............................................4
1.3
Kurzbeschreibung des Applets ..............................................................................5
1.4
Ziel des Applets .....................................................................................................6
Visualisierungen mit dem Applet............................................................... 7
2.1
Normalverteilte Daten............................................................................................7
2.2
Abweichungen von der Normalverteilung ..............................................................8
2.3
Logarithmische Normalverteilung ..........................................................................8
2.4
Weibullverteilung ...................................................................................................9
Auswertung eigener Daten ....................................................................... 9
Wahrscheinlichkeitsnetz
2
1
Statistischer Hintergrund
1.1
Verteilungen
Daten wie z.B. Versuchsergebnisse, Messwerte für Länge und Gewicht von Teilen,
maximale Leistung eines Motors u.ä. unterliegen immer einer Zufallsstreuung – auch wenn
versucht wurde, möglichst unter identischen Bedingungen zu arbeiten und nichts zu
verändern. Trägt man die Häufigkeit, mit der einzelne Werte auftreten, grafisch auf, so
Häufigkeitsdichte
erhält man ein Histogramm.
Histogramm:
0.3
0.2
relative
0.1
bestimmter Messwert oder ein Wert in
0
einem bestimmten Bereich aufgetreten
25 26 27 28 29 30 31 32 33 34 35
Häufigkeit,
mit
der
ein
ist
Dicke
Sammelt man immer mehr Daten (idealisiert unendlich viele), so wird aus der
Häufigkeitsdichte die Verteilungsdichte.
Häufig liefert die Normalverteilung eine gute Näherung für die Verteilung der Daten (siehe
dazu das Applet „Zentraler Grenzwertsatz“). Die Dichte der Normalverteilung ist gegeben
durch
g( x ) =
1
2π ⋅ σ
⋅e
−
( x − μ)2
2σ 2
wobei
μ = Mittelwert und
σ = Standardabweichung (bzw. σ2 = Varianz) der Normalverteilung
zwei Parameter sind, die Lage bzw. Breite der Verteilung beschreiben. Folgende Bilder
zeigen die Dichte der Normalverteilung für verschiedene Mittelwerte μ bzw. für
verschiedene Standardabweichungen σ.
Verteilungsdichte
Wahrscheinlichkeitsnetz
3
μ = 27
0,2
35
Dichte der Normalverteilungen
mit Mittelwerten μ = 27, 30 und
35 °C, Standardabweichung σ =
2 °C
0,1
0
25
Verteilungsdichte
30
30
Dicke [μm]
35
Dichte der Normalverteilungen
mit Mittelwert μ = 30 °C und
Standardabweichungen
σ = 1, 2 und 4 °C
0,4
σ=1
0,3
0,2
2
0,1
4
0
25
30
Dicke [μm]
35
Zuverlässigkeitsdaten und Festigkeitsdaten werden häufig in guter Näherung von
der logarithmischen Normalverteilung oder der Weibullverteilung beschrieben.
Bei
der
logarithmischen
Normalverteilung
ist
der
Logarithmus
des
Messwerts
normalverteilt. Die Dichte der logarithmischen Normalverteilung ist gegeben durch
g( x ) =
1
1
⋅e
2π ⋅ σ x
⋅
−
(ln x − μ ) 2
2σ 2
wobei
μ = Mittelwert und
σ =Standardabweichung (bzw. σ2 = Varianz) der Verteilung von ln x.
Die Weibullverteilung ist eine Extremwertverteilung, sie beschreibt die Verteilung des
schwächsten Gliedes einer Kette. Die Dichte der Weibullverteilung ist gegeben durch
g( t ) =
wobei
β ⎛ t − t0 ⎞
⋅⎜
⎟
T ⎝ T ⎠
β −1
⎛ t−t0
− ⎜⎜
⋅e ⎝ T
⎞
⎟⎟
⎠
β
Wahrscheinlichkeitsnetz
4
T = charakteristische Lebensdauer
β = Formparameter und
t0 = ausfallfreie Zeit.
1.2
Darstellung von Daten im Wahrscheinlichkeitsnetz
Bei der Auswertung von Versuchs- oder Messergebnissen ist es schwer, anhand eines
Histogramms zu beurteilen, ob die Daten zu einer Normalverteilung oder einer anderen
Verteilung passen. Im Wahrscheinlichkeitsnetz für normalverteilte Daten sind die Achsen
nun so skaliert, dass eine Normalverteilung auf eine Gerade abgebildet wird. Daten, die
aus einer Normalverteilung stammen, streuen daher nur zufällig um eine Gerade. Da eine
Gerade leichter zu erkennen ist als die oben dargestellten Verteilungskurven, kann man
leichter erkennen, ob die vorliegenden Daten zu einer Normalverteilung passen. Das
folgende Bild zeigt ein Beispiel für Daten, die nur zufällig von einer Normalverteilung
abweichen. Als Interpretationshilfe ist eine Gerade eingezeichnet.
Auch für andere Verteilungen kann
man geeignete Achsenskalierungen
wählen, sodass die Verteilung auf
eine Gerade abgebildet wird. Im
Applet
können
dieselben
Daten
wahlweise in einem Wahrscheinlichkeitsnetz für normalverteilte Daten,
logarithmisch normalverteilte Daten
und
weibullverteilte
Daten
einge-
tragen werden.
Für die logarithmische Normalverteilung ist die x-Achse logarithmisch skaliert, bei der
Weibullverteilung ist zusätzlich die y-Achse so skaliert, dass weibullverteilte Daten auf
einer Geraden liegen.
Wahrscheinlichkeitsnetz
1.3
5
Kurzbeschreibung des Applets
In das Applet können unter „Dateneingabe“ beliebige Daten (Stichprobenwerte) von Hand
eingegeben werden (richtigen Stichprobenumfang angeben und dann „neu berechnen“)
oder Zufallszahlen mit vorgegebener Verteilung simuliert werden. Die Daten können dann
wahlweise im „Wahrscheinlichkeitsnetz für NV“, „Wahrscheinlichkeitsnetz für log-NV“ oder
im „Wahrscheinlichkeitsnetz für Weibull“ dargestellt werden.
Verteilungsdichte
Folgende Verteilungen können für die Simulation vorgegeben werden:
Standardabweichung σ
σ
Normalverteilung mit Mittelwert μ und
Verteilungsdichte
Verteilungsdichte
Normalverteilung mit Mittelwert μ und
μ
xu
μ
xo
Standardabweichung σ, bei xu und xo
beschnitten
σ
außerhalb
(entsteht,
dieser
wenn
Grenzen
Teile
aussortiert
wurden)
Anteil p
μ1
Überlagerung von zwei Normalverteilun-
μ2
Anteil 1-p
σ1
σ2
gen – Mischverteilung, ein Anteil p der Teile stammt aus Normalverteilung mit Mittelwert μ1 und Standardabweichung σ1, der
Rest aus Normalverteilung mit Mittelwert
Verteilungsdichte
μ2 und Standardabweichung σ2
μ=1, σ=1
logarithmische
Normalverteilung
–
in
diesem Beispiel hat die Verteilung von ln x
den Mittelwert μ=1 und die Standardabweichung σ=1
Verteilungsdichte
Wahrscheinlichkeitsnetz
to
6
T
β=2
Weibullverteilung mit ausfallfreier Zeit t0,
charakteristischer Lebensdauer T und in
Verteilungsdichte
diesem Beispiel Formparameter β=2
Verteilungsdichte
xu
xo
Rechteckverteilung (Gleichverteilung) mit
Untergrenze xu und Obergrenze xo
Dreieckverteilung mit Untergrenze xu und
Obergrenze xo
xu
1.4
xo
Ziel des Applets
Das Applet soll dabei helfen, Daten ins Wahrscheinlichkeitsnetz einzutragen. Es soll den
Zusammenhang zwischen der Form der Verteilung und der Skalierung des zugehörigen
Wahrscheinlichkeitsnetzes verdeutlichen und grafisch zeigen, dass
•
Daten aufgrund der Zufallsstreuung immer von der Geraden abweichen
•
diese Abweichungen aber mit zunehmendem Stichprobenumfang n immer kleiner
werden, wenn die Stichprobe aus der jeweiligen Verteilung entnommen wurde
•
abweichende Verteilungen zu einer Abweichung von der Geraden führen
•
diese Abweichung bei kleinem Stichprobenumfang n aber nicht von der Zufallsstreuung unterscheidbar ist.
Wahrscheinlichkeitsnetz
7
2
Visualisierungen mit dem Applet
2.1
Normalverteilte Daten
Nach dem Start des Applets wählen Sie "Eingabe der Verteilungen (Simulation)" und
Normalverteilung mit z.B. μ=10 und σ=2, mit einem Stichprobenumfang von 1000.
Im "Wahrscheinlichkeitsnetz für NV" liegen die Punkte näherungsweise auf einer Geraden.
"Neu berechnen" gibt ähnliche Punkte, die ebenfalls geringfügig von der Geraden
abweichen. Beachten Sie dabei, dass die Abweichungen bei kleinen und bei großen
Prozentwerten nur scheinbar größer sind als bei mittleren Werten – die y-Skala ist hier
gestreckt. Die Einzelwerte unterliegen einer Zufallsstreuung, insgesamt wird die Verteilung
aber gut beschrieben. Man kann zwar keine Aussagen über Einzelwerte treffen, wohl aber
über viele Werte zusammen.
Im "Wahrscheinlichkeitsnetz für log-NV" und "Weibull" erhält man eine deutlich erkennbare
systematische Abweichung von einer Geraden – diese Verteilungen sind nicht konsistent
mit den Daten.
Wiederholen Sie die Simulation nun mit einem Stichprobenumfang von 20. Die Streuung
der Werte um die Gerade im "Wahrscheinlichkeitsnetz für NV" ist deutlich größer, im
"Wahrscheinlichkeitsnetz für log-NV" und "Weibull" ist die Abweichung von der Geraden
nicht mehr eindeutig erkennbar: Bei kleinem Stichprobenumfang ist die Zufallsstreuung
größer, die Form der Verteilung ist kaum mehr zu erkennen.
Einfacher grafischer Test auf Konsistenz von Daten mit der verwendeten Verteilung:
Wenn die größte Abweichung eines Punktes (in %, nicht mm im Bild) kleiner ist als ca.
89/ n , dann sind die Daten mit der angenommenen Verteilung konsistent (vereinfachter
Kolmogoroff-Smirnov-Lilliefors-Test). Achtung: Dies ist kein Beweis dafür, dass die
Verteilung richtig ist, es liegt nur kein Widerspruch vor – ein Beweis ist prinzipiell nicht
möglich.
Testen Sie diesen Test, indem Sie für verschiedene Stichprobenumfänge n bei mehreren
Simulationen jeweils die größte Abweichung bestimmen und mit der Grenze vergleichen.
Wahrscheinlichkeitsnetz
2.2
8
Abweichungen von der Normalverteilung
Eine beschnittene Normalverteilung tritt in der Praxis auf, wenn eine Fertigung so stark
streut, dass auch Teile außerhalb der Toleranz auftreten, diese dann aber aussortiert
werden. Eine Mischung von zwei Normalverteilungen tritt auf, wenn Teile von zwei
Fertigungslinien oder Herstellern vermischt werden, die sich wesentlich unterscheiden.
Rechteckverteilung und Dreieckverteilung treten kaum praktisch auf und dienen hier nur
als Demonstrationsbeispiele.
Für all diese Verteilungen gilt: Bei großem Stichprobenumfang sind die Abweichungen von
der Normalverteilung (und den anderen Verteilungen) klar erkennbar – insbesondere,
wenn die Abweichung groß ist (bei der beschnittenen Verteilung z.B. wenn xo bei μ+σ liegt,
bei der Mischverteilung wenn μ1 und μ2 sich um mehr als σ unterscheiden). Bei kleinem
Stichprobenumfang sind die Abweichungen nur schwer erkennbar. Als Entscheidungshilfe
können Sie den Kolmogoroff-Smirnov-Lilliefors-Test aus Abschnitt 2.1 verwenden.
Experimentieren Sie mit unterschiedlichen Abweichungen von der Normalverteilung und
versuchen Sie jeweils die charakteristischen Abweichungen von der Geraden im
"Wahrscheinlichkeitsnetz für NV" zu verstehen (die beschnittene Verteilung und die
Rechteckverteilung sind an den Rändern zu steil, die Mischverteilung hat ein Plateau im xBereich zwischen μ1 und μ2).
2.3
Logarithmische Normalverteilung
Wählen Sie "log-Normalverteilung" z.B. mit μ=1 und σ=1. Bei der Eintragung in das
"Wahrscheinlichkeitsnetz für NV" ist eine deutliche Abweichung von der Gerade
erkennbar, bei der Eintragung in das "Wahrscheinlichkeitsnetz für log-NV" liegen die
Werte auf einer Geraden: Im "richtigen" Netz liegen die Werte auf einer Geraden – so
kann man die Form der Verteilung grafisch ermitteln. x ln ist der Mittelwert von ln x und
schätzt μ − da die Achse mit den x-Werten beschriftet ist, liest man dort eμ ab. sln ist die
Standardabweichung von ln x und schätzt σ.
Wahrscheinlichkeitsnetz
2.4
9
Weibullverteilung
Wählen Sie "Weibull" z.B. mit β=2 und T=10 und zunächst t0=0. Bei der Eintragung in das
"Wahrscheinlichkeitsnetz für NV" ist eine deutliche Abweichung von der Gerade
erkennbar, bei der Eintragung in das "Wahrscheinlichkeitsnetz für log-NV" weniger
deutlich
und
bei
"Weibull"
liegen
die
Werte
auf
einer
Geraden.
Bei
Zuverlässigkeitsuntersuchungen werden sowohl das "Wahrscheinlichkeitsnetz für log-NV"
als auch "Weibull" verwendet, da sie in mancher Hinsicht ähnlich sind und bei den
geringen
Stückzahlen
bei
Zuverlässigkeitsuntersuchungen
manchmal
schwer
zu
unterscheiden sind. "Weibull" ist theoretisch besser geeignet und wesentlich weiter
verbreitet.
Verwenden Sie nun als ausfallfreie Zeit t0=10. Mit keinem der Netze erhält man zunächst
eine befriedigende Gerade. Im Weibullnetz befindet sich jedoch unten ein Schieber für t0.
Verschieben Sie diesen nun und beobachten Sie, wie die zeitverschobene Kurve (orange)
sich einer Gerade annähert, wenn t0 ca. 10 ist: So kann die ausfallfreie Zeit empirisch
ermittelt werden.
3
Auswertung eigener Daten
Wenn Sie "Eingabe von Stichprobenwerten" wählen, können Sie Ihre eigenen Daten
eingeben und in den drei Netzen darstellen. Untersuchen Sie so die Verteilung Ihrer
Daten. Dazu müssen Sie vorher den richtigen Stichprobenumfang wählen.