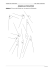Übungsaufgabe 23 (Thalessatz und Umkehrung des Thalessatzes)

Übung zum Lehrerweiterbildungskurs ’Geometrie’
WiSe 2014/2015
Aufgabe 23 (Thalessatz und Umkehrung des Satzes von Thales)
(u.a. Skript-Aufg. 64 )
1. Beweisen Sie den Satz von Thales:
In der euklidischen Ebene ist jeder Umfangswinkel im Halbkreis ein
rechter Winkel.
Lösungshinweis: Zerlegen Sie das zugehörige Dreieck in zwei gleichschenklige Dreiecke und wenden Sie den Winkelsummensatz an (s. Figur (a))!
2. Beweisen Sie die Umkehrung des Satzes von Thales:
Ist in einem Dreieck △ABC der euklidischen Ebene der Winkel bei C
ein rechter Winkel, so liegt C auf dem Kreis mit AB als Durchmesser.
Lösungshinweis: Siehe Figur (b)! Zum Nachweis der Existenz des Schnittpunktes S dürfen Sie hier benutzen, dass jede Tangente, also eine den
Kreis in genau einem Punkt schneidende Gerade, auf dem zugehörigen
Durchmesser senkrecht steht.
C
(a)
C
S
(b)
Lösungsskizze:
1. Sei M der Mittelpunkt des Durchmessers AB des gegebenen Halbkreises. Die Dreiecke △AM C und △BM C sind gleichschenklig. Daher gilt
g(∢M AC) = g(∢M CA) =: α und g(∢M BC) = g(∢M CB) =: β.
Wegen M ∈ [A, B] addieren sich die Winkel ∢ACM und ∢M CB zu
einem Winkel der Größe α + β. Aus dem Winkelsummensatz, angewandt auf das Dreieck △ABC, folgt (α + β) + α + β = 2R und daraus
∢ACB = R.
2. 1. Möglichkeit:
Würden beide Geraden AC und BC des gegebenen rechtwinkligen Dreiecks ∆ := △ABS den Kreis über AB nicht in einem Punkt ungleich
A bzw. B schneiden, so stünden sie (gemäß der Lösungshilfe) auf AB
senkrecht und könnten nicht Träger der Seiten von ∆ sein. Also exisiert der Schnittpunkt S mindestens einer beiden Geraden mit dem
Kreis. Das Dreieck △ABS ist nach dem Thalessatz rechtwinklig; damit
besäße das Dreieck △ACS zwei rechte Innenwinkel, ein Widerspruch
zum Winkelsummensatz für Dreiecke.
□
2. Möglichkeit:
Aus dem gegebenen rechtwinkligen Dreieck konstruiere man durch Antragen rechter Winkel an AC in A und an BC in B ein Rechteck. Dessen
Diagonalen halbieren sich in M und sind kongruent. Da die Strecken
AM und CM also gleich lang sind, liegt C auf einem Halbkreis um M
mit Radius |AM |.
2