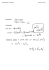763101P Fysiikan matematiikkaa kesä 2015 Jakso 9 Näytä laskut
Transcription
763101P Fysiikan matematiikkaa kesä 2015 Jakso 9 Näytä laskut
763101P Fysiikan matematiikkaa kesä 2015 Jakso 9 Näytä laskut viimeistään torstaina 4.6. tai palauta ne viimeistään perjantaina 5.6. Vektorit ja differentiaalilaskenta 1. Origosta alkunopeudella v 0 v 0 x ˆi v 0 y ˆj v 0 z kˆ heitetyn kappale radiusvektori r (t ) on muotoa 1 r(t ) gt 2kˆ v 0t , 2 missä g 10 m/s2 on maan vetovoiman kiihtyvyys. Olkoot alkunopeuden komponentit v 0 x 5 m/s, v 0 y 5 m/s ja v 0 z 20 m/s. a) Totea, että SI-yksiköissä kappaleen lentorata (radiusvektori) on r(t ) 5t ˆi 5t ˆj 5(4t t 2 ) kˆ . b) Laske kappaleen nopeus, vauhti ja kiihtyvyys ajan hetkellä t 3 s. c) Millä ajan hetkellä kappale on lakikorkeudessa? Vihje: Lakikorkeudessa z-suuntainen nopeus on nolla. 2. Tarkastellaan tehtävän 1 lentorataa. a) Määritä lentoradan tangenttivektori T . Mikä on tangenttivektorin yksikkö? b) Mihin suuntaan kappale lentää lakikorkeudessaan? Esitä tulos tangenttivektorin avulla. c) Mihin suuntaan kappale lentää sillä hetkellä, kun se osuu maahan. Oletetaan, että maan pinta on xy-taso (ks. kuva yllä). 3. Kuinka pitkän matkan tehtävän 1 kappale lentää ilmassa, ts. kuinka pitkä on radiusvektorin kärjen piirtämä käyrä origosta maahanosumispisteeseen? 4 Aputulos: 18 16 x 4 x 2 dx 10, 248 0 4. Tarkastellaan origokeskistä R-säteistä ympyrää, jonka kehän pisteet ( x, y) saadaan yhtälöistä x( ) R cos ja y( ) R sin . Laske käyrän r( ) x( )ˆi y( )ˆj kaaren pituus välillä 0 2 . 5. Laske tehtävän 4 ympyrän yksikkötangentti, kaarevuus, kaarevuussäde ja päänormaali ensin yleisessä pisteessä ja sitten erikoistapauksena pisteessä, jossa . 6. Laske käyrän y x 2 kaarevuussäde ja päänormaali pisteessä x 0 . Ohje: Käyrän piirtää vektori r( x) xˆi x 2 ˆj . Vastaukset 1. a) osoita b) nopeus 5 ˆi 5 ˆj 10 kˆ (m/s) vauhti 5 6 (m/s) kiihtyvyys 10 kˆ (m/s2) c) lakikorkeudessa, kun t 2 s 2. a) b) c) ˆi ˆj (4 2t )kˆ 2 (4 2t ) 2 , laaduton 1 ˆ ˆ (i j) 2 1 ˆ ˆ (i j 4kˆ ) 3 2 3. 5 10, 248 51 (m) 4. 2 R 5. yksikkötangentti ( sin )ˆi (cos )ˆj kaarevuus 1/ R kaarevuussäde R päänormaali ( cos )ˆi ( sin )ˆj 6. 1/ 2 ja N ˆj = jˆ , kun = 1/ R , kun = R , kun = î , kun